Nevezetes eloszlások
1. feladat. Sűrűségfüggvény.
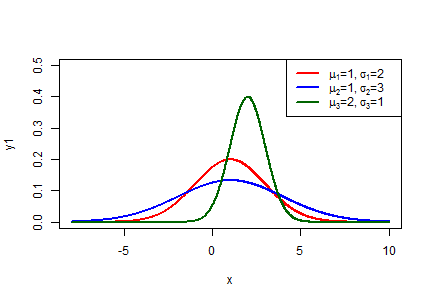
Egyetlen ábrán jelenítsünk meg 3 db normális eloszláshoz tartozó sűrűségfüggvényt, melyek paraméterei: \(\mu_1=1\), \(\sigma_1=2\); \(\mu_2=1\), \(\sigma_2=3\); \(\mu_3=2\), \(\sigma_3=1\)
x <- seq(from = -8, to = 10, by = 0.01)
y1 <- dnorm(x = x, mean = 1, sd = 2)
y2 <- dnorm(x = x, mean = 1, sd = 3)
y3 <- dnorm(x = x, mean = 2, sd = 1)
plot(x = x, y = y1, type = "l", ylim=c(0, 0.5), col="red", lwd=2)
lines(x = x, y = y2, type = "l", col="blue", lwd=2)
lines(x = x, y = y3, type = "l", col="darkgreen", lwd=2)
legend("topright",
legend = c(expression(paste(mu[1], "=1, ", sigma[1], "=2 ")),
expression(paste(mu[2], "=1, ", sigma[2], "=3 ")),
expression(paste(mu[3], "=2, ", sigma[3], "=1 "))),
col=c("red", "blue", "darkgreen"), lwd=2)
2. feladat. Sűrűségfüggvény.
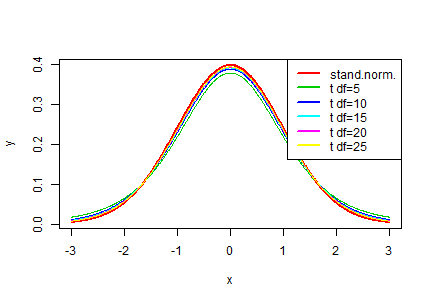
Mutassuk be a standard normális eloszlás és a t eloszlás kapcsolatát! Egy ábrán jelenítsük meg a standard normális eloszlás sűrűségfüggvényét és az 5, 10, 15, 20 és 25 szabadsági fokú t eloszlás sűrűségfüggvényét!
x <- seq(from = -3, to = 3, by = 0.01)
y <- dnorm(x = x, mean = 0, sd = 1)
y1 <- dt(x = x, df = 5)
y2 <- dt(x = x, df = 10)
y3 <- dt(x = x, df = 15)
y4 <- dt(x = x, df = 20)
y5 <- dt(x = x, df = 25)
plot(x = x, y = y, type = "l", col=2, lwd=2)
lines(x = x, y = y1, type = "l", col=3)
lines(x = x, y = y2, type = "l", col=4)
lines(x = x, y = y3, type = "l", col=5)
lines(x = x, y = y4, type = "l", col=6)
lines(x = x, y = y5, type = "l", col=7)
legend("topright",
legend =c("stand.norm.", "t df=5",
"t df=10", "t df=15", "t df=20", "t df=25") ,
col=2:7, lwd=2)
3. feladat. Sűrűségfüggvény.
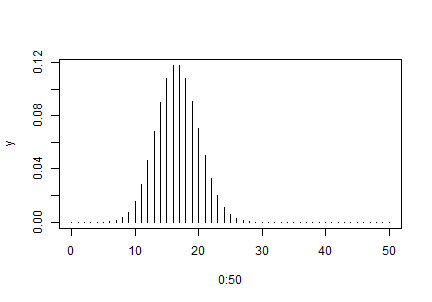
Jelenítsük meg az \(n=50\), \(p=1/3\) paraméterű binomiális eloszlás eloszlását bemutató vonalas ábrát!
y <- dbinom(x = 0:50, size = 50, prob = 1/3)
plot(x = 0:50, y, type = "h")
4. feladat. Sűrűségfüggvény.
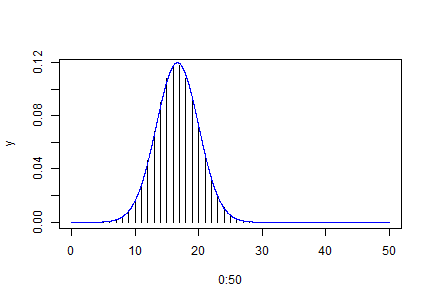
Jelenítsük meg az \(n=50\), \(p=1/3\) paraméterű binomiális eloszlás eloszlását bemutató vonalas ábrát! Rajzoljuk be rá a közelítő normalis eloszás görbéjét is!
y <- dbinom(x = 0:50, size = 50, prob = 1/3)
plot(x = 0:50, y, type = "h")
x <- seq(0, 50, 0.01)
y <- dnorm(x, mean = 50*1/3, sd=sqrt(50*1/3*2/3))
lines(x, y, col="blue")
5. feladat. Sűrűségfüggvény.
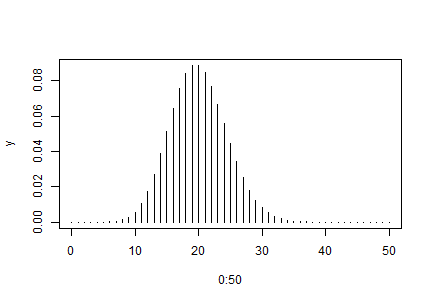
Jelenítsük meg a \(\lambda=1/100\) paraméterű Poisson eloszlás eloszlását bemutató vonalas ábrát!
y <- dpois(x = 0:50, lambda = 20)
plot(x = 0:50, y, type = "h")
6. feladat. Sűrűségfüggvény.
Egy szabályos pénzérmét 6-szor egymás után feldobunk? Mi a valószínűsége, hogy pontosan 2 fejet kapunk?
dbinom(x = 2, size = 6, prob = 1/2)
[1] 0.234375
7. feladat. Sűrűségfüggvény.
Egy szabályos pénzérmét 6-szor egymás után feldobunk? Mi a valószínűsége, hogy 3-nál kevesebb fejet kapunk?
dbinom(x = 0, size = 6, prob = 1/2) +
dbinom(x = 1, size = 6, prob = 1/2) +
dbinom(x = 2, size = 6, prob = 1/2)
[1] 0.34375
8. feladat. Sűrűségfüggvény.
Egy szabályos pénzérmét 6-szor egymás után feldobunk? Mi a valószínűsége, hogy 4-nél több fejet kapunk?
dbinom(x = 5, size = 6, prob = 1/2) + dbinom(x = 6, size = 6, prob = 1/2)
[1] 0.109375
9. feladat. Sűrűségfüggvény.
Egy kollégiumban a diákok 60%-a lány. Mi a valószínűsége, hogy 10 tagú tanulócsoportban pontosan 4 lány van?
dbinom(x = 4, size = 10, prob = 0.6)
[1] 0.1114767
10. feladat. Sűrűségfüggvény.
Egy kollégiumban a diákok 60%-a lány. Mi a valószínűsége, hogy 10 tagú tanulócsoportban pontosan 5, 6 vagy 7 lány van?
dbinom(x = 5, size = 10, prob = 0.6) +
dbinom(x = 6, size = 10, prob = 0.6) +
dbinom(x = 7, size = 10, prob = 0.6)
[1] 0.6664716
11. feladat. Sűrűségfüggvény.
Egy kollégiumban a diákok 60%-a lány. Mi a valószínűsége, hogy 10 tagú tanulócsoportban legalább 5 lány van?
dbinom(x = 5, size = 10, prob = 0.6) +
dbinom(x = 6, size = 10, prob = 0.6) +
dbinom(x = 7, size = 10, prob = 0.6) +
dbinom(x = 8, size = 10, prob = 0.6) +
dbinom(x = 9, size = 10, prob = 0.6) +
dbinom(x = 10,size = 10, prob = 0.6)
[1] 0.8337614
12. feladat. Sűrűségfüggvény.
Tegyük fel, hogy LeBron James a szabaddobások 73%-át értékesíti. Mi a valószínűsége, hogy a következő 8 szabaddobásból pontosan 6-ot fog értékesíteni?
dbinom(x = 6, size = 8, prob = 0.73)
[1] 0.3089034
13. feladat. Sűrűségfüggvény.
Tegyük fel, hogy LeBron James a szabaddobások 73%-át értékesíti. Mi a valószínűsége, hogy a következő 8 szabaddobásból legalább 6-ot fog értékesíteni?
dbinom(x = 6, size = 8, prob = 0.73) +
dbinom(x = 7, size = 8, prob = 0.73) +
dbinom(x = 8, size = 8, prob = 0.73)
[1] 0.6281732
14. feladat. Sűrűségfüggvény.
Tegyük fel, hogy LeBron James a szabaddobások 73%-át értékesíti. Mi a valószínűsége, hogy a következő 8 szabaddobásból legalább 2-t fog értékesíteni?
1-(dbinom(x = 0, size = 8, prob = 0.73) + dbinom(x = 1, size = 8, prob = 0.73))
[1] 0.9993609
15. feladat. Sűrűségfüggvény.
Tegyük fel, hogy LeBron James a szabaddobások 73%-át értékesíti. Mi a valószínűsége, hogy a következő 8 szabaddobásból legalább 2-t fog értékesíteni?
1-(dbinom(x = 0, size = 8, prob = 0.73) + dbinom(x = 1, size = 8, prob = 0.73))
[1] 0.9993609
16. feladat. Sűrűségfüggvény.
Egy 10 kérdésből álló tesztben minden kérdésre 4 lehetséges válasz közül kell megjelölni az egyetlen helyest. Mi a valószínűsége, hogy egy olyan diák, aki véletlenszerűen adja meg a válaszokat, pontosan 2 kérdésre válaszol helyesen?
dbinom(x = 2, size = 10, prob = 1/4)
[1] 0.2815676
17. feladat. Sűrűségfüggvény.
Egy 10 kérdésből álló tesztben minden kérdésre 4 lehetséges válasz közül kell megjelölni az egyetlen helyest. Mi a valószínűsége, hogy egy olyan diák, aki véletlenszerűen adja meg a válaszokat, 3-nál kevesebb kérdésre válaszol helyesen?
dbinom(x = 0, size = 10, prob = 1/4) +
dbinom(x = 1, size = 10, prob = 1/4) +
dbinom(x = 2, size = 10, prob = 1/4)
[1] 0.5255928
18. feladat. Eloszlásfüggvény.
Egy szabályos pénzérmét 6-szor egymás után feldobunk? Mi a valószínűsége, hogy 3-nál kevesebb fejet kapunk?
pbinom(q = 2, size = 6, prob = 1/2)
[1] 0.34375
19. feladat. Eloszlásfüggvény.
Egy szabályos pénzérmét 6-szor egymás után feldobunk? Mi a valószínűsége, hogy 4-nél több fejet kapunk?
1-pbinom(q = 4, size = 6, prob = 1/2)
[1] 0.109375
pbinom(q = 4, size = 6, prob = 1/2, lower.tail = F)
[1] 0.109375
20. feladat. Eloszlásfüggvény.
Egy kollégiumban a diákok 60%-a lány. Mi a valószínűsége, hogy 10 tagú tanulócsoportban legalább 5 lány van?
1-pbinom(q = 4, size = 10, prob = 0.6)
[1] 0.8337614
pbinom(q = 4, size = 10, prob = 0.6, lower.tail = F)
[1] 0.8337614
21. feladat. Eloszlásfüggvény.
Tegyük fel, hogy LeBron James a szabaddobások 73%-át értékesíti. Mi a valószínűsége, hogy a következő 8 szabaddobásból legalább 6-ot fog értékesíteni?
1-pbinom(q = 5, size = 8, prob = 0.73)
[1] 0.6281732
pbinom(q = 5, size = 8, prob = 0.73, lower.tail = F)
[1] 0.6281732
22. feladat. Eloszlásfüggvény.
Tegyük fel, hogy LeBron James a szabaddobások 73%-át értékesíti. Mi a valószínűsége, hogy a következő 8 szabaddobásból legalább 2-t fog értékesíteni?
1-pbinom(q = 1, size = 8, prob = 0.73)
[1] 0.9993609
pbinom(q = 1, size = 8, prob = 0.73, lower.tail = F)
[1] 0.9993609
23. feladat. Eloszlásfüggvény.
Egy 10 kérdésből álló tesztben minden kérdésre 4 lehetséges válasz közül kell megjelölni az egyetlen helyest. Mi a valószínűsége, hogy egy olyan diák, aki véletlenszerűen adja meg a válaszokat, 3-nál kevesebb kérdésre válaszol helyesen?
pbinom(q = 2, size = 10, prob = 1/4)
[1] 0.5255928
24. feladat. Eloszlásfüggvény.
A \(Z\) valószínűségi változó legyen standard normális eloszlású! Mennyi a \(P(Z<3)\) valószínűség?
pnorm(q = 3, mean = 0, sd = 1)
[1] 0.9986501
25. feladat. Eloszlásfüggvény.
A \(Z\) valószínűségi változó legyen standard normális eloszlású! Mennyi a \(P(Z>1)\) valószínűség?
1 - pnorm(q = 1, mean = 0, sd = 1)
[1] 0.1586553
26. feladat. Eloszlásfüggvény.
A \(Z\) valószínűségi változó legyen standard normális eloszlású! Mennyi a \(P(-2<Z<2)\) valószínűség?
pnorm(q = 2, mean = 0, sd = 1) - pnorm(q = -2, mean = 0, sd = 1)
[1] 0.9544997
27. feladat. Eloszlásfüggvény.
Egy populációban a testmagasság várható értéke 175 cm, szórása 17 cm! Mi a valószínűsége, hogy egy véletlenszerűen választott személy 190 cm-nél magasabb?
1-pnorm(q = 190, mean = 175, sd = 17)
[1] 0.188793
28. feladat. Eloszlásfüggvény.
Egymintás u-próba végrehajtása során a próbastatisztika értéke \(u=1,79\). Határozzuk meg a p értéket, kétoldali ellenhipotézis mellett!
2*(1-pnorm(q = 1.79, mean = 0, sd = 1))
[1] 0.07345391
29. feladat. Eloszlásfüggvény.
Egymintás u-próba végrehajtása során a próbastatisztika értéke \(u=1,79\). Határozzuk meg a p értéket, baloldali ellenhipotézis mellett!
pnorm(q = 1.79, mean = 0, sd = 1)
[1] 0.963273
30. feladat. Eloszlásfüggvény.
Egymintás u-próba végrehajtása során a próbastatisztika értéke \(u=1,79\). Határozzuk meg a p értéket, jobboldali ellenhipotézis mellett!
1-pnorm(q = 1.79, mean = 0, sd = 1)
[1] 0.03672696
31. feladat. Eloszlásfüggvény.
Egymintás u-próba végrehajtása során a próbastatisztika értéke \(u=-2,31\). Határozzuk meg a p értéket, kétoldali ellenhipotézis mellett!
2*pnorm(q = -2,31, mean = 0, sd = 1)
[1] 0.04550026
32. feladat. Eloszlásfüggvény.
Egymintás u-próba végrehajtása során a próbastatisztika értéke \(u=-2,31\). Határozzuk meg a p értéket, baloldali ellenhipotézis mellett!
pnorm(q = -2,31, mean = 0, sd = 1)
[1] 0.02275013
33. feladat. Eloszlásfüggvény.
Egymintás u-próba végrehajtása során a próbastatisztika értéke \(u=-2,31\). Határozzuk meg a p értéket, jobboldali ellenhipotézis mellett!
1-pnorm(q = -2,31, mean = 0, sd = 1)
[1] 0.9772499
34. feladat. Eloszlásfüggvény.
Egy 35 elemű mintán, kétoldali ellenhipotézissel végrehajtott t próbában a próbastatisztika értéke \(t=2,45\). Határozzuk meg a p értéket!
2*(1-pt(q = 2.54, df=34))
[1] 0.01582348
35. feladat. Eloszlásfüggvény.
Egy 35 elemű mintán, baloldali ellenhipotézissel végrehajtott t próbában a próbastatisztika értéke \(t=2,45\). Határozzuk meg a p értéket!
pt(q = 2.54, df=34)
[1] 0.9920883
36. feladat. Eloszlásfüggvény.
Egy 35 elemű mintán, jobboldali ellenhipotézissel végrehajtott t próbában a próbastatisztika értéke \(t=2,45\). Határozzuk meg a p értéket!
1-pt(q = 2.54, df=34)
[1] 0.007911739
37. feladat. Eloszlásfüggvény.
Egy 70 elemű mintán, kétoldali ellenhipotézissel végrehajtott t próbában a próbastatisztika értéke \(t=-1,97\). Határozzuk meg a p értéket!
2*pt(q = -1.97, df=69)
[1] 0.0528533
38. feladat. Eloszlásfüggvény.
Egy 70 elemű mintán, baloldali ellenhipotézissel végrehajtott t próbában a próbastatisztika értéke \(t=-1,97\). Határozzuk meg a p értéket!
pt(q = -1.97, df=69)
[1] 0.02642665
39. feladat. Eloszlásfüggvény.
Egy 70 elemű mintán, jobboldali ellenhipotézissel végrehajtott t próbában a próbastatisztika értéke \(t=-1,97\). Határozzuk meg a p értéket!
1-pt(q = -1.97, df=69)
[1] 0.9735733
40. feladat. Eloszlásfüggvény.
Egy 50 elemű mintán, jobboldali ellenhipotézissel végrehajtott \(\chi^2\) próbában a próbastatisztika értéke \(\chi^2=110.7\). Határozzuk meg a p értéket!
1-pchisq(q = 110.7, df=49)
[1] 1.136809e-06
41. feladat. Eloszlásfüggvény.
Egy jobboldali ellenhipotézissel végrehajtott F próbában a próbastatisztika értéke \(F=1.78\), a számláló szabadsági fokainak száma 17, a nevezőé 12. Határozzuk meg a p értéket!
1-pf(q = 1.78, df1 = 17, df2 = 12)
[1] 0.1567035
42. feladat. Kvantilis.
Az egymintás u próbát hajtunk végre kétoldali ellenhipotézissel. A szignifikanciaszint \(\alpha=0,05\). Melyek az elfogadási tartomány határai?
qnorm(0.05/2)
[1] -1.959964
qnorm(1-0.05/2)
[1] 1.959964
43. feladat. Kvantilis.
Az egymintás u próbát hajtunk végre baloldali ellenhipotézissel. A szignifikanciaszint \(\alpha=0,05\). Mi lesz az elfogadási tartomány határa?
qnorm(0.05)
[1] -1.644854
44. feladat. Kvantilis.
Az egymintás u próbát hajtunk végre jobboldali ellenhipotézissel. A szignifikanciaszint \(\alpha=0,05\). Mi lesz az elfogadási tartomány határa?
qnorm(1-0.05)
[1] 1.644854
45. feladat. Véletlen számok.
Tegyük fel, hogy a testmagasság normális eloszlású változó 175 cm várható értékkel és 17 cm szórással. Válasszunk 40 véletlen testmagasságot ebből az eloszlásból! Rajzoljunk hisztogramot és simított hisztogramot a mintára!
x <- rnorm(n = 40, mean = 175, sd = 17)
hist(x)

plot(density(x))
