Korrelációszámítás
1. feladat. Felkészülés vizsgára.
A következő táblázat 6 hallgató két adatát tartalmazza: mennyit órát töltött egy adott vizsgára készülésre, illetve a vizsga eredményét! Számoljuk ki a korrelációs együttható értékét és vizsgáljuk a szignifikanciáját!
| Felkészüléssel töltött idő (óra) | Vizsga eredménye |
|---|---|
| 3 | 86 |
| 5 | 95 |
| 4 | 92 |
| 4 | 83 |
| 2 | 78 |
| 3 | 82 |
Kiszámuljuk a minta alapján a korrelációs együtható értékét, majd a következő hipotézist teszteljük:
- \(H_0:\rho=0\)
- \(H_1: \rho \neq 0\)
Adatok előkészítése
# széles adattábla létrehozása
felkeszules <- c(3, 5, 4, 4, 2, 3)
eredmeny <- c(86, 95, 92, 83, 78, 82)
d <- data.frame(felkeszules, eredmeny)
d
felkeszules eredmeny
1 3 86
2 5 95
3 4 92
4 4 83
5 2 78
6 3 82
Mutatók meghatározása
library(psych)
describeData(d)
n.obs = 6 of which 6 are complete cases. Number of variables = 2 of which all are numeric TRUE
variable # n.obs type H1 H2 H3 H4 T1 T2 T3 T4
felkeszules 1 6 1 3 5 4 4 4 4 2 3
eredmeny 2 6 1 86 95 92 83 92 83 78 82
describe(d)
Description of d
Numeric
mean median var sd valid.n
felkeszules 3.5 3.5 1.1 1.05 6
eredmeny 86.0 84.5 41.2 6.42 6
cor(d$felkeszules, d$eredmeny) # korrelációs együttható
[1] 0.8615551
Grafikus segítség
Pontdiagram rajzolása
library(ggplot2)
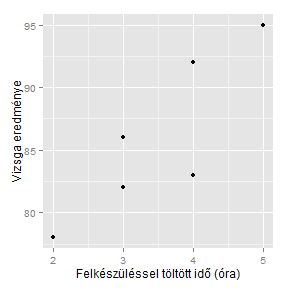
ggplot(data = d, aes(x = felkeszules, y = eredmeny)) +
geom_point() + labs(x="Felkészüléssel töltött idő (óra)", y="Vizsga eredménye")
Hipotézisvizsgálat
cor.test(d$felkeszules, d$eredmeny)
Pearson's product-moment correlation
data: d$felkeszules and d$eredmeny
t = 3.3942, df = 4, p-value = 0.02742
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.1662054 0.9846467
sample estimates:
cor
0.8615551
A felkészülési idő és a vizsga eredménye között a korrelációs együttható értéke \(r=0,86\). A populációbeli korrelációs együttható szignifikánsan különbözik nullától (\(p=0,0274\)), azaz kapcsolat van a felkészülési idő és a vizsga eredménye között.