3. Klasszikus tesztelmélet

A klasszikus tesztelméletben az alapfeltevés, hogy a mérni kívánt konstruktum mérhető, és a mért konstruktumnak van egy, a tesztkitöltőre jellemző értéke, azaz egy úgynevezett valódi értéke, és a mérés célja ezen valódi érték meghatározása. (Ezért a klasszikus tesztelméletet gyakran nevezik valódi érték elméletnek is.) Mivel a valódi pontérték a gyakorlatban sohasem ismert pontosan, a mért érték (a mérés eredménye) úgy határozható meg, mint a valódi érték és egy mérési hiba összege, ami annak kifejezése, hogy a mérési folyamat feltehetően nem tökéletes.

\[X = T + \epsilon\]

ahol X a tapasztalati, megfigyelt tesztpontszám, T a valódi érték, és ε hibatag.

A mérések kapcsán két féle hibát szoktak megkülönböztetni. Szisztematikus hiba, vagy torzított mérésről akkor beszélünk, ha a mérés során elkövetett hiba nem random, hanem valamilyen irányba szisztematikusan torzít, például ha a tesztkitöltők előre ismerik a kérdéseket, vagy azok egy részét, vagy a tesztkitöltő rövidlátó és ezért nem tudja megfelelően elolvasni és értelmezni az instrukciót, és/vagy a kérdéseket. Az ilyen esetekben a mért értékek rendre hajlamosak felfelé, illetve lefelé eltérni a valódi pontértéktől. A nemszisztematikus hiba ezzel szemben azt jelenti, hogy bár a mérés nem tökéletes, de az eltérések iránya és mértéke teljesen véletlenszerű, azaz ilyen esetben a mérés várható értéke megegyezik a valódi értékkel.

A klasszikus tesztelmélet az alábbi axiómákon alapul (pl. Münnich mtsai, 2002):

\[\epsilon \sim N(0, \sigma)\]

A mérési hiba nulla átlagú normál eloszlást követ.

\[ \rho_{T\epsilon}=0 \]

A mérési hiba független a valódi értéktől.

\[ \rho_{\epsilon\epsilon'}=0 \] Független mérések esetén a mérési hibák is függetlenek.

3.1. Megbízhatóság

A klasszikus tesztelméletben az egyik alapvető jellemző a mérőeszköz megbízhatósága. Megbízhatóságon legáltalánosabban az úgynevezett teszt-reteszt megbízhatóságot értjük, ami azt fejezi ki, hogy milyen együttjárás van az egyik tesztfelvétel során, illetve egy következő tesztfelvétel során elért tesztpontszámok között. Ez a korreláció természetesen feltehetően pozitív, és értéke minél közelebb van 1-hez, annál megbízhatóbbnak tekinthető a mérőeszköz. Azonban az ismételt tesztfelvétel ugyanazon teszt alanyokkal, azonos körülmények között gyakorlatilag nehezen kivitelezhető, és erőforrásigényes, ezért más módszerre van szükség a kérdés megválaszolására.

Egy lehetséges megoldás a megbízhatóság becslésére a tesztfelezéses eljárás lehet (Brown, 1910; Spearman, 1910). A módszer lényege, hogy a mérőeszközt két tesztrészre lehet osztani, az egyes tesztrészekre kiszámítani a tesztpontszámokat, majd a két tesztrészen elért tesztpontszámok korrelációja kiszámolható. Ez a megbízhatóság egy belső konzisztencia megközelítése. Azonban az ilyen módon számolt korreláció nagy változatosságot mutathat attól függően, hogy hogyan történik a mérőeszköz két részre osztása, mivel ez önkényesen történhet. A probléma egy lehetséges megoldása, ha valamennyi lehetséges tesztfelezést végrehajtjuk, minden tesztfelezés esetén kiszámítjuk a tesztrészek tesztpontszámát és ezek korrelációját. Az összes lehetséges tesztfelezés esetén számolt korrelációk átlaga felhasználható belső konzisztencia mutatóként, de ez nyilvánvalóan egy nagyon időigényes megoldás a megbízhatóság becslésére.

A teszt-reteszt megbízhatóság és a tesztfelezéses módszer kapcsán jelentkező problémák kiküszöbölésére számos együtthatót javasoltak a megbízhatóság jellemzésére. Az egyik legismertebb ilyen együttható a KR20 formula (Kuder & Richardson, 1937), ami a Cronbach (1951) által javasolt alfa együttható alapja volt. A Cronbach alfa együttható mindmáig a legismertebb, leginkább elfogadott és legszélesebb körben alkalmazott belső konzisztencia mutató, ami megtalálható a standard statisztikai szoftverekben. A Cronbach alfa a következő módon számolható:

\[\alpha=\frac{I}{I-1}\Big(1-\frac{\sum_{i=1}^{I}var(x_i)}{var(X)}\Big)\]

ahol I az itemek száma, x_i az i-ikitem, és X a teszt összpontszáma.

A Cronbach alfa együttható kétségtelen népszerűsége mellett fontos megemlíteni, hogy bizonyos problémák is felmerülnek a Cronbach alfa alkalmazása kapcsán. Az egyik ilyen jellegzetesség a Cronbach alfa azon tulajdonsága, hogy az együttható értéke az itemszám függvényében változik, hosszabb, több itemet tartalmazó teszt megbízhatósága magasabb lesz, mint hasonló itemeket tartalmazó, de rövidebb teszt megbízhatósága. Ezt a jelenséget már Brown (1910) és Spearman (1910) is felfedezték és a következő formulát alkották a jelenség leírására:

\[rel(X_{ntimes}) =\frac{n rel(X)}{1+(n-1)rel(X)}\]

A Spearman-Brown formula felhasználható tesztfelezéses módszerrel történő megbízhatóság becslésben, feltételezve, hogy a felezés eredményeként kapott tesztrészek párhuzamos teszteknek tekinthetők, vagyis olyan teszteknek, amik ugyanazt a mögöttes látens konstruktumot, ugyanolyan módon mérik. Az alfa együttható értékét szintén befolyásolhatja az itemek skálája, ami nehezítheti az együttható értelmezését, mivel az alfa együttható elfogadható mértéke változhat a teszt hosszúságának és az itemek skálájának függvényében. Általában az alfa együttható elvárt értéke legalább 0,8, de a 0,7 feletti értékeket már elfogadhatónak szokták tekinteni. Elméletileg annál jobb, minél közelebb van az együttható értéke 1-hez, de a gyakorlatban a túl magas alfa érték is problémás lehet, mivel ez azt jelzi, hogy az itemek praktikusan pontosan ugyanazt mérik, vagyis akár egyetlen item is ugyanolyan jól mérheti a mögöttes a konstruktumot, mint a hosszabb teszt. (Münnich és mtsai, 2002)

Egy másik, a Cronbach alfa együttható alkalmazásához kapcsolódó probléma, hogy a megfelelően magas alfa értéket a teszt egydimenziósságának bizonyítékaként kezelik, vagyis, hogy a teszt egyetlen mögöttes konstruktumot mér, ami nem feltétlenül helytálló. Magas alfa érték akkor is előfordulhat, ha a mérőeszköz több különböző látens konstruktumot mér.

A mérőeszköz dimenzionalitásának vizsgálata jellemzően főkomponens analízissel, illetve faktor analízissel történik (lásd lent, a skálaszerkesztés fejezetben).

Annak szemléltetésére, hogy hogyan lehet a klasszikus tesztelmélet bizonyos mutatóit kiszámolni, egy 79 tesztkitöltő a Center for Epidemiologic Studies Depresszió Skála 16 itemére adott válaszait tartalmazó adatmátrixot használunk. (Az eredeti skála 20 itemet tartalmaz, de a fordított (pozitív megfogalmazású) itemeket nem tartalmazza az adatmátrix.)

Az adatmátrix 16 iteme 0 és 3 közötti értéket vehet fel, a magasabb értékek az állításban megfogalmazott értékek elmúlt egy hétbeli gyakoribb előfordulását jelzik.

Az adatmátrix első hat sora a következőképpen néz ki:

head(df)

##   V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16
## 1  3  3  3  3  3  3  3  3  3   3   3   3   3   3   3   3
## 2  2  1  2  2  2  2  3  2  2   1   1   1   0   2   1   1
## 3  2  0  2  2  2  2  1  1  1   1   0   0   1   2   1   2
## 4  2  3  2  2  3  1  0  1  1   2   2   0   2   2   1   2
## 5  2  0  1  1  2  2  1  1  0   1   1   1   1   1   1   1
## 6  2  2  2  2  3  3  3  2  2   1   1   2   2   3   3   3

A Cronbach alfa együttható (például) az RcmdrMisc R csomag (Fox, 2020) reliability függvénye használható.

RcmdrMisc::reliability(cov(df))$alpha

##     alpha 
## 0.8370298

Amint az R eredményben látható, a Cronbach alfa együttható értéke meglehetősen magas, 0,84, azaz a 16 itemes skála a depressziómegbízható mérőeszköze.

3.1.1. A mérés standard hibája a klasszikus tesztelméletben

A klasszikus tesztelméletben a mérési hiba az alkalmazott mérőeszköz megbízhatóságának és a tesztpontszámok szórásának segítségével számolható:

\[SE=\sigma X * \sqrt{(1-\alpha)} \]

A fent bemutatott, depressziót mérő skála esetén a mérés standard hibájának számítása az R szoftver segítségével a következőképpen alakul:

total <- rowSums(df) # tesztpontszámok számítása
sigma <- sd(total)   # tesztpontszámok szórása 
alpha <- RcmdrMisc::reliability(cov(df))$alpha # megbízhatóság számítása

SE <- sigma*sqrt(1-alpha)
SE

##    alpha 
## 3.413832

Vagyis a 16 itemes depresszió skála standard mérési hibája 3.41. Ezen érték ismeretében már számolható konfidencia intervallum a depresszió teszten elért becsült depresszió értékekre. Például a depresszió skálánkon elért 20-as összpontszám esetén 95%-os konfidencia intervallum a következőképpen számítható:

CI1 <- 20 -1.96*SE  # a 95%-os konfidencia intervallum alsó végpontja
CI2 <- 20 + 1.96*SE # a 95%-os konfidencia intervallum felső végpontja
CI1

##    alpha 
## 13.30889

CI2

##    alpha 
## 26.69111

3.2. Érvényesség

A megbizhatóság mellett a klasszikus tesztelméleten alapuló tesztek másik fontos mutatója a teszt érvényessége. Míg a megbízhatóság azt fejezi ki, hogy mennyire jól, pontosan tudjuk mérni a mérni kívánt konstruktumot, az érvényesség arra utal, hogy mennyire sikerül azt mérnünk, amit mérni szeretnénk.

Az esetek egy jelentős részében úgy erősíthető meg, hogy a mérőeszköz megfelelő mérőeszköze a mérni kívánt konstruktumnak, hogy keresünk egy olyan jellemzőt, ami ugyanazt, vagy legalábbis hasonló konstruktumot ragad meg, mint a mérőeszközünk, és kapcsolatot keresünk ki ezen jellemző és a mérőeszköz által kapott tesztpontszámok között. Ennek a kapcsolatnak a jellemzésére természetes módon adódik a korreláció alkalmazása, ami ilyen módon az érvényesség fokmérője lesz.

Tételezzük fel, hogy az intelligenciát szeretnénk mérni, és létrehozunk egy mérőeszközt erre a célra. Amikor elkészültünk az eszközünkkel, kereshetünk olyan jellemzőket, amikről megalapozottan feltételezhető, hogy kapcsolatban állnak az intelligenciával. Ez lehet például az iskolai teljesítmény, amiről jogosan feltételezhető, hogy, legalábbis bizonyos mértékben, az intelligencia (és persze számos egyéb tényező) által meghatározott. Tehát amit tehetünk, hogy meghatározzuk a létrehozott mérőeszközünkön elért összpontszámot, és kiszámoljuk az összpontszámok tanulmányi átlaggal való együttjárását, hogy alátámasszuk az általunk alkotott mérőeszköz érvényességét.

Ezt a típusú érvényességet kritérium érvényességnek nevezzük, mivel egy kritériumot (ebben az esetben a tanulmányi átlagot) használjuk a mérőeszköz validálására. A klasszikus tesztelmélet ezen mutatója a megbízhatósághoz hasonlóan szintén korreláció alapú mutató.

3.3. Skálaszerkesztés

A klasszikus tesztelmélet keretében a főkomponens analízis (PCA; pl. Münnich, Nagy & Abari, 2006) gyakran alkalmazott eljárás a skálaszerkesztés során. Az eljárás egyik előnye, hogy alkalmas lehet a mérőeszköz egydimenziósságának vizsgálatára, ami fontos, mivel általános feltételezés a klasszikus tesztelméletben, hogy a teszt vagy skála egyetlen mögöttes látens jellemzőt mér. Az eljárás másik előnye, hogy segítségével az itemekből súlyozott skálaérték számolható, ami az egyszerű, súlyozatlan összegzéssel ellentétben az itemek relatív fontosságát is figyelembe veszi (pl. Münnich és mtsai, 2002).

A PCA egy matematikai eljárás, melynek célja az itemek, változók egy csoportjában lévő információ kivonása, sűrítése. Az eljárás eredményeképpen az I darab kezdeti korreláló változóból I darab nem-korreláló változó, úgynevezett főkomponens számítódik. A k-ik főkomponens a következőképpen számolható:

\[PC_k = w_{1k}X_1+w_{2k}X_2+w_{3k}X_3+ ... +w_{Ik}X_{I}\]

ahol PC_k a k-ik főkomponens, w_ik az i-ik item súlya a k-ik főkomponens esetén, és X_i az i-ik kezdeti változó.

A w_ik itemsúlyok értékének meghatározása úgy történik, hogy az eredményül kapott főkomponens varianciája a lehető legnagyobb legyen. Mivel ez a feltétel azt eredményezné, hogy a w_ik itemsúlyokat minden határon túl növeljük, ezért szükséges korlátozni a súlyok maximális értékét a következőképpen:

\[ \sum_{i=1}^{I}{w_{ik}^2}=1 \]

vagyis a súlyok négyzeteinek összege egy kell, hogy legyen valamennyi főkomponens esetén.

A főkomponensek számítása során fontos, hogy a súlyozást úgy kell megtenni, hogy a keletkező főkomponens független legyen valamennyi további főkomponenstől, azaz korrelációjuk 0 legyen, így a főkomponensek a kezdeti változók által hordozott információ független részeit képviselik.

A főkomponens analízis során fontos annak vizsgálata, hogy hány főkomponens lehet érdekes a további felhasználás szempontjából. Az egyik módszer ennek eldöntésére a főkomponensek varianciáinak ábrázolása, és annak vizsgálata, hogy van-e jelentős „törés” az ábrán, azaz, van-e olyan főkomponens, vagy főkomponensek, amelyek kiemelkednek a varianciájuk tekintetében. Ez az eljárás az úgynevezett könyök módszer. Egy másik lehetőség az egy fölötti varianciával rendelkező főkomponensek megkeresése. Az eljárás hátterében az az elv áll, hogy ha a főkoponens analízist a változók korrelációs mátrixára hajtjuk végre, vagy standardizált változók kovariancia mátrixát használjuk, akkor az egyes kezdeti változók által hordozott információ egységnyi, tehát ennél kisebb varianciájú főkomponenssel nincs értelme foglalkozni.

Az R szoftverben többféleképpen is lehetséges főkomponens analízist végrehajtani, itt a stats csomag (R Core Team, 2021) princomp függvénye segítségével mutatjuk be az eljárást.

# főkomponens analízis a df adattábla itemeire (korrelációs mátrixra)
p.c.a <- princomp(df, cor = TRUE) 

# főkomponensek varianciáinak ábrázolása
barplot(p.c.a$sdev^2, col = "steelblue", las = 2)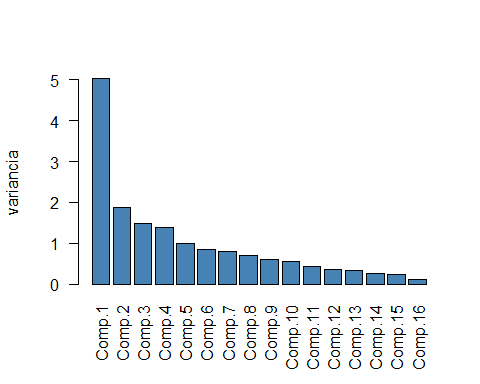

1. ábra. A főkomponensek varianciáinak oszlopdiagramja

A könyök módszer alapján az 1. ábra varianciáit elemezve arra a következtetésre juthatunk, hogy a depresszió itt használt 16 itemes mérőeszköze egydimenziósnak tekinthető, mivel a főkomponensek varianciáiban nagy különbség van az első két főkomponens esetén, míg a továbbis főkomponensek varianciái már csak kismértékű csökkenést mutatnak. A főkomponensek variancia értékeit figyelmbe véve azonban már egy négy dimenziós mögöttes struktúra sem zárható ki, mivel az első négy főkomponens is egynél nagyobb varianciát mutat. Figyelembe véve, hogy a 16 item négy tartalmilag némileg elkülönülő aspektusát ragadja meg a depressziónak ez az eredmény szinkronban lehet az elmélettel.

A főkomponens analízis eredményeit további célokra is felhasználhatjuk a dimenzionalitás vizsgálatán túl. Az egyik ilyen felhasználási lehetőség a főkomponens súlyok használata a főkomponens értékek kiszámítására, annak érdekében, hogy a súlyozott összegként számított skálaérték kifejezze az egyes itemek relatív fontosságát. Fontos megemlíteni, hogy az algoritmus sajátosságai miatt a súlyozott skála az eredetihez képest megfordulhat, ezt fontos ellenőrizni.

# súlyozott skálaértékek (wss) számítása és hozzáadása az depresszió adattáblához 
df$wss <- round(p.c.a$scores[, 1], 2)

# az adattábla első hat sora 
head(df)

##   V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16   wss
## 1  3  3  3  3  3  3  3  3  3   3   3   3   3   3   3   3  5.51
## 2  2  1  2  2  2  2  3  2  2   1   1   1   0   2   1   1  0.09
## 3  2  0  2  2  2  2  1  1  1   1   0   0   1   2   1   2 -0.96
## 4  2  3  2  2  3  1  0  1  1   2   2   0   2   2   1   2  0.04
## 5  2  0  1  1  2  2  1  1  0   1   1   1   1   1   1   1 -1.80
## 6  2  2  2  2  3  3  3  2  2   1   1   2   2   3   3   3  2.98

A főkomponens analízis eredmények egy újabb felhasználása lehet egy megbízhatósági mutató számítása az első főkomponens súlyának felhasználásával.

\[ \theta = \frac{I}{I-1}(1-\frac{1}{\lambda_1}) \]

ahol I az itemek száma és \(\lambda_i\) az első főkomponens súlya.

A θ megbízhatósági együttható egy pontosabb becslését adja a skála valódi megbízhatóságának, mint a Cronbach alfa, ami alulról becsüli a megbízhatóságot. Az alfa együtthatóval szemben a θ megbízhatósági együttható az egydimenziósságot is alátámaszthatja.

# a theta megbízhatósági együttható számítása
nitems <- 16
theta <- (nitems/(nitems-1)) * (1 - 1/p.c.a$sdev[1]^2)
theta

##    Comp.1 
## 0.8546059

3.4. Tesztpontszámok értelmezése

Amikor teszteket használunk pszichológiai konstruktumok mérésére, az egyik kritikus kérdés a tesztpontszámok értelmezése.

A tesztpontszám, mint nyers pontérték bizonyos esetekben informatív lehet, például olyan esetekben, amikor a tesztpontszám a helyesen megoldott feladatok számát jelenti, ami a tesztkitöltők képesség- vagy teljesítményértékelésének alapja lehet. Ez a fajta értelmezés például szakértői véleményen alapulhat. Sok esetben van arra mód, hogy meghatározzunk bizonyos küszöbértékeket, teljesítmény standardokat, amik egyfajta minimum elvárásként fogalmazhatók meg ahhoz, hogy valaki sikeresen átmenjen egy vizsgán, például. Amennyiben a küszöbértéket nem éri el a tesztkitöltő nem mehet át a vizsgán és ez akkor is igaz, ha minden tesztkitöltő megbukik. (Bár egy ilyen, vagy hasonló eset komoly kérdéseket vetne fel a teszt megfelelő voltát, és/vagy a teszt által mért tudás átadásának minőségét tekintve.) (Cronbach, 1990.)

Azonban a helyes válaszok alapján számolt összpontszám nem feltétlenül informatívak, amikor a tesztelés célja az egyéni különbségek mérése, a tesztkitöltő populációhoz viszonyított eredményének meghatározása, elhelyezése a populációban. Ilyen esetekben a tesztkitöltő eredménye egy standardhoz, vagy normához hasonlítható. A teszteredmények normaalapú értelmezése széles körben alkalmazott, és előnye, hogy a teljesítmény relatív értékelése akkor is használható, ha nincsenek világosan meghatározható teljesítménykritériumok a mért konstruktum esetén.

A tesztpontszámok normaalapú értelmezése esetén számos eljárás használható a nyers pontszámok transzformálására, hogy olyan értéket rendeljünk a tesztkitöltőhöz, amely kifejezi a normához viszonyított relatív pozíciójukat. Az egyik ilyen módszer az adatok jól ismert standardizálása, amikor a nyers adatokat z értékekké transzformáljuk, a tesztkitöltő nyers pontértékéből kivonva a nyers pontértékek átlagát, és elosztva a nyers pontértékek szórásával. A z értékek értelmezése viszonylag könnyű, mivel ezek egy standard normál eloszlásbeli értékek (z ~ N(0, 1) ). Egy másik népszerű módszer a nyers tesztpontszámok transzformálására a T értékké történő átalakítás. Ez a transzformáció a fent leírt standardizáláson alapul, de ebben az esetben a nyers értékek egy 50-es átlagú és 10-es szórású normál eloszlásra projektáljuk. Szintén hasonló megoldás nyers tesztpontszámok IQ esetén használt 100-as átlagú és 15-ös szórású normál eloszlásra történő projekciója. Ezek a módszerek feltételezik, hogy a populációban a tesztpontszámok normál eloszlást követnek.

A percentilis értékek használata szintén népszerű módszer a tesztpontértékek normaalapú értelmezésére. A percentilis a normaként szolgáló minta azon tagjainak százalékos aránya, akik egy adott nyers tesztpontértéket, vagy annál alacsonyabbat érnek el. (Amennyiben a normaként szolgáló minta több mint egy tagja ér el egy nyers pontértéket, akkor az ezen értéket elérők felét tekintik úgy, mint aki ezt, vagy ennél kisebb tesztpontszámot ért el.) Ez egy meglehetősen intuitív módszer, aminek eredménye nagyon könnyen értelmezhető, és nem érzékeny a normál eloszlás sérülésére.

Egy újabb lehetőség a nyers tesztpontszámok könnyebben értelmezhető értékre transzformálására az úgynevezett „standard kilenc” (ST9; stanine) skála használata. Ez az átalakítás szintén a standardizáláson alapul. Az ST9 értékeket úgy kaphatjuk meg, ha a z értékek skáláját 0,5 szórás szélességű intervallumokra osztjuk a 2. ábrán látható módon. Az egyes intervallumokban feltüntetett százalékos értékek azt mutatják, hogy a populáció körülbelül mekkora hányada éri el az adott ST9 értéket.

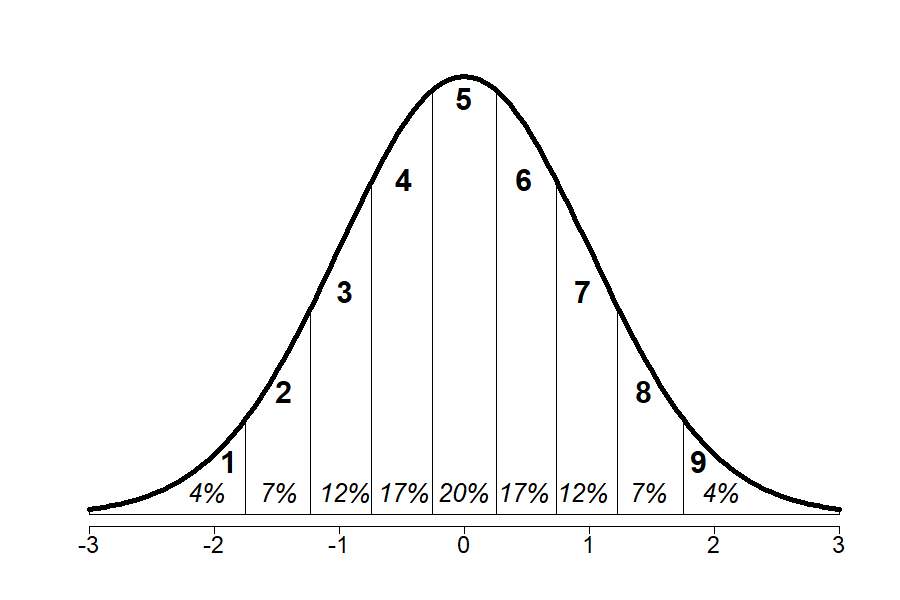
2. ábra. A Standard Nine skála az értékek százalékos arányával

Mint látható, mindezen transzformációk célja, hogy elősegítse a tesztkitöltő populációhoz viszonyított helyének, vagy legalábbis a referenciaként használt normatív mintához viszonyított relatív pozíciójának meghatározását. Fontos megjegyezni, hogy a fenti transzformációk, a percentilisek kivételével, az adatok normál eloszlását feltételezik, ami az esetek jelentős részében tartható, de nem minden esetben. Amennyiben a nyers tesztpontértékek nem normál eloszlásúak, lehetőség van a nyers tesztpontértékek normál eloszlásúra transzformálására. A normalizált értékek úgy számolhatók ki, hogy első lépésként kiszámoljuk a tapasztalati kumulatív valószínűségeket minden nyers pontérték esetén, aztán megkeressük, hogy az adott kumulatív valószínűség milyen értékhez tartozik egy normál (legvalószínűbb esetben standard normál) eloszlás esetén. A nyers pontértékeket ezután arra a normál eloszlásbeli értékre transzformáljuk, amelyikhez ugyanaz a kumulatív valószínűség tartozik, mint az adott nyers pontértékhez. Ha a normalizálás során standard normál eloszlást használunk, eredményül normalizált standard értékeket kapunk. Fontos megemlíteni, hogy amennyiben normalizálást alkalmazunk nagyon fontos ezt figyelembe venni az eredmények értelmezése során.

3.5. Tesztpontszámok megfeleltetése

A tesztelések során nem ritka, hogy egy adott konstruktumot mérő tesztnek több mint egy változatát használják fel. Több tesztváltozat kialakításának legáltalánosabb oka, hogy szeretnék elkerülni, hogy például azok, akik későbbi időpontban töltik ki a tesztet, vagy újra kell tesztelni valakit egy idő elteltével, az esetleg ismerje a teszt itemeit, és így torzítsa a becslést. Ugyanazon teszt alternatív verzióinak használata jó megoldásnak tekinthető a nemkívánatos előnyök elkerülésére. Bármilyen vonzó is azonban az alternatív verziók alkalmazása, ez nehézséget okozhat, amikor a tesztpontszámokat kell értelmezni, vagy ha a pontszámok tesztverziók közötti összehasonlítására van szükség. Ennek oka, hogy bár a tesztverziók kialakítása úgy történik, hogy egymásnak a legteljesebb mértékben megfelelők legyenek, aligha lehetséges tökéletesen ekvivalens tesztverziók kialakítása. Ezen a ponton válik szükségessé a tesztpontszám megfeleltetés, azaz kapcsolatot kell találni a tesztverziók között, azaz meghatározni, hogy az A tesztverzión elért adott pontszám milyen pontszámnak felel meg a B tesztverzión. Két, ugyanazon teszt különböző verzióján elért tesztpontszám akkor tekinthető ekvivalensnek, ha az ezen pontokat elérő tesztkitöltők populációbeli relatív pozíciója megegyezik.

A klasszikus tesztelméletben két népszerű módszer van az ekvivalencia kialakítására. Az első eljárást lineáris megfeleltetésnek nevezik. A módszer lényege, hogy az adott, A tesztverzión elért tesztpontszámot standardizáljuk, majd megkeressük azt a B tesztverzión elért pontszámot, amelyiknek ugyanaz a standardizált értéke.

\[ \frac{x_A-\mu_A}{\sigma_A}=\frac{x_B-\mu_B}{\sigma_B} \]

ahol x_A az A tesztverzión elért tesztpontszám, amelynek megfelelő értéket keressük, µ_A az A tesztverzión elért tesztpontszámok átlaga, σ_A pedig az A tesztverzión elért tesztpontszámok szórása. A B indexszel jelölt szimbólumok a megfelelő értékek a B tesztverzió esetén. A fenti egyenletből az x_B érték a következőképpen számolható:

\[ x_B=\frac{x_A-\mu_A}{\sigma_A}\sigma_B+\mu_B \]

A másik népszerű tesztpontszám megfeleltetési módzser a klasszikus tesztelméletben az ekvipercetilis megfeleltetés, ami, mint neve is sugallja, a percentilisek számításán alapul. Mint a percentilisek számítási módjából következik, egy A tesztverzión elért pontszám akkor tekinthető ekvivalensnek egy B tesztverzión elért pontszámmal, ha azonos a percentilis értékük.

A tesztpontszám megfeleltetés kivitelezése során különböző vizsgálati elrendezések alkalmazhatók. A személyek közötti vizsgálati elrendezés, amikor a vizsgálati személyeket véletlenszerűen két csoport egyikébe sorolják (feltéve, hogy két tesztverzió összevetéséről van szó), egy természetes választás. A véletlenszerűen kialakított csoportok egyike az A tesztverziót tölti ki, míg a másik a B tesztverziót. Amennyiben megfelelően nagy minta áll rendelkezésre, és a vizsgálatba bevont résztvevők véletlenszerű csoportba sorolása biztosított, addig tartható a feltételezés, hogy a két csoport ekvivalensnek tekinthető, és ebben az esetben a csoportok teszteredményei közötti esetleges különbségek csakis a tesztverziók különbségeiből eredhetnek, és végrehajtható a tesztpontszám megfeleltetés. Egy másik megoldás az ekvivalens csoportok kialakításának problémájára a személyen belüli kísérleti elrendezés, ahol a vizsgálati személyek több kísérleti feltételben is részt vesznek, vagyis két csoport (két tesztverzió) esetén a vizsgálati személyek mindkét tesztverziót kitöltik. Ez az eljárás biztosítja, hogy a tesztverziókat kitöltő csoportok biztosan ekvivalensek, mivel ugyanazok a vizsgálati személyek alkotják a csoportokat. Problémák azonban személyen belüli elrendezés estén is adódhatnak. A legjellemzőbb probléma a sorrendi hatás, vagyis amikor az, hogy milyen sorrendben történik a tesztkitöltés, hatással lehet a tesztverziókon elért eredményekre. A probléma kiküszöbölésére valamilyen kiegyensúlyozás, két tesztverzió esetén fordított kiegyensúlyozás használható, amikor a tesztkitöltőket véletlenszerűen két csoportba soroljuk, és az egyik csoport tagjai A tesztverzió, majd B tesztverzió sorrendben töltik ki a teszteket,míg a másik csoport tagjai B tesztverzió, majd A tesztverzió sorrendben töltik ki a teszteket. Más megoldások szintén lehetségesek, ilyen például a tesztverziók itemeinek összekeverése.