4. Item-válasz elmélet

Az item-válasz elmélet (Item Response Theory; IRT; pl. Embretson & Reise, 2000), vagy más néven látens vonás elmélet (latent trait theory, pl. Borsboom, 2008), egy frissebb a tesztszerkesztésben és –értékelésben használt tesztelméleti megközelítés. A klasszikus tesztelmélettel szemben, ahol az elemzés egysége a teljes teszt, és annak jellemzői (pl. megbízhatóság, érvényesség) vannak a középpontban, az item-válasz elméletben a fókusz a teszt legkisebb egységén, az itemen van, az itemek jellemzőit, paramétereit modellek illesztésével becslik. Az item-válasz elmélet eredetileg elsősorban teljesítményteszt jellegű mérőeszközök esetén volt használatos, ahol meghatározható, hogy mi a helyes válasz, és így az első IRT modellek kétértékű, dichotóm (helyes/helytelen) változók elemzését célozták. Bár az IRT modellek nem kizárólag képesség/teljesítmény jellegű tesztek esetén használhatók, hanem például attitűdök, személyiségvonások, stb. esetén is, a továbbiakban a mérni kívánt látens változóra képességként, míg a mögöttes látens tartalom irányába mutató választ korrekt, míg az azzal ellentétes választ inkorrekt válasznak nevezzük, még ha a szó szoros értelmében nem határozható meg helyes válasz. Az item-válasz elméletben a cél az itemek paramétereinek becslése és ezen információk felhasználása tesztek létrehozására és végső soron a teszkitöltő képességének becslésére. Az item-válasz elmélet nagy előnye, hogy az ebben alkalmazott modellek segítségével item bankokat lehet létrehozni, és ezekből az itembankokból az itemeket célirányosan a mérési problémának megfelelően összeválogatva könnyen lehet finomhangolni a mérőeszközöket a célnak és a mérni kívánt populációnak megfelelően. Szintén lehetőség van adaptív tesztelés kivitelezésére, amikor a tesztkitöltő képességbecslése minden item után frissíthető, és a következő item a frissen becsült képességnek megfelelően választható ki. Ez az eljárás lehetővé teszi a képesség megbízható becslését viszonylag kevés item használatával.

4.1. Dichotóm változók esetén alkalmazott IRT modellek

A legegyszerűbb IRT modell az egyparaméteres logisztikus modell (1PL; Rasch, 1960). Ebben a modellben az itemre adott helyes válasz valószínűsége a tesztkitöltő képességének, és az item nehézségének a függvénye.

\[P(x=1|\theta_p,\beta_i)=\frac{e^{(\theta_p-\beta_i)}}{1+e^{(\theta_p-\beta_i)}}\]

ahol θ_p a p-ik személy képességparamétere és β_i az i-ik item nehézségparamétere. Ha a fenti modellt ábrázoljuk az itemjelleggörbét (ICC) kapjuk, ami az item-válasz elmélet egyik alapkoncepciója. A 3. ábrán egy itemjelleggörbe példa látható. A nehézségparaméter a képesség segítségével definiálható, azzal a képességel egyenlő, amely képességgel rendelkező személyek fele tudja helyesen, megválaszolni az itemet, vagyis azzal a képességgel egyenlő, amely képesség esetén az itemre adott helyes válasz valószínűsége ,5. A nehézségparaméter értéke a XXX ábrán a szaggatott vonalak segítségével könnyen leolvasható, értéke 0. Az egyparaméteres logisztikus modell esetén az itemek itemjelleggörbéi egybevágóak, csak elhelyezkedésükben (nehézségükben) különböznek a képességparaméter mentén.

Amennyiben nem csak az itemjellegörbe elhelyezkedése (nehézség), hanem meredeksége (diszkriminációja) is különbözhet itemenként a kétparaméteres logisztikus modellhez (2PL)  jutunk, ahol a modell kibővül az itemspecifikus α_i diszkriminációs paraméterrel (Birnbaum, 1968).

\[P(x=1|\theta_p,\beta_i, \alpha_i)=\frac{e^{\alpha_i(\theta_p-\beta_i)}}{1+e^{\alpha_i(\theta_p-\beta_i)}}\]

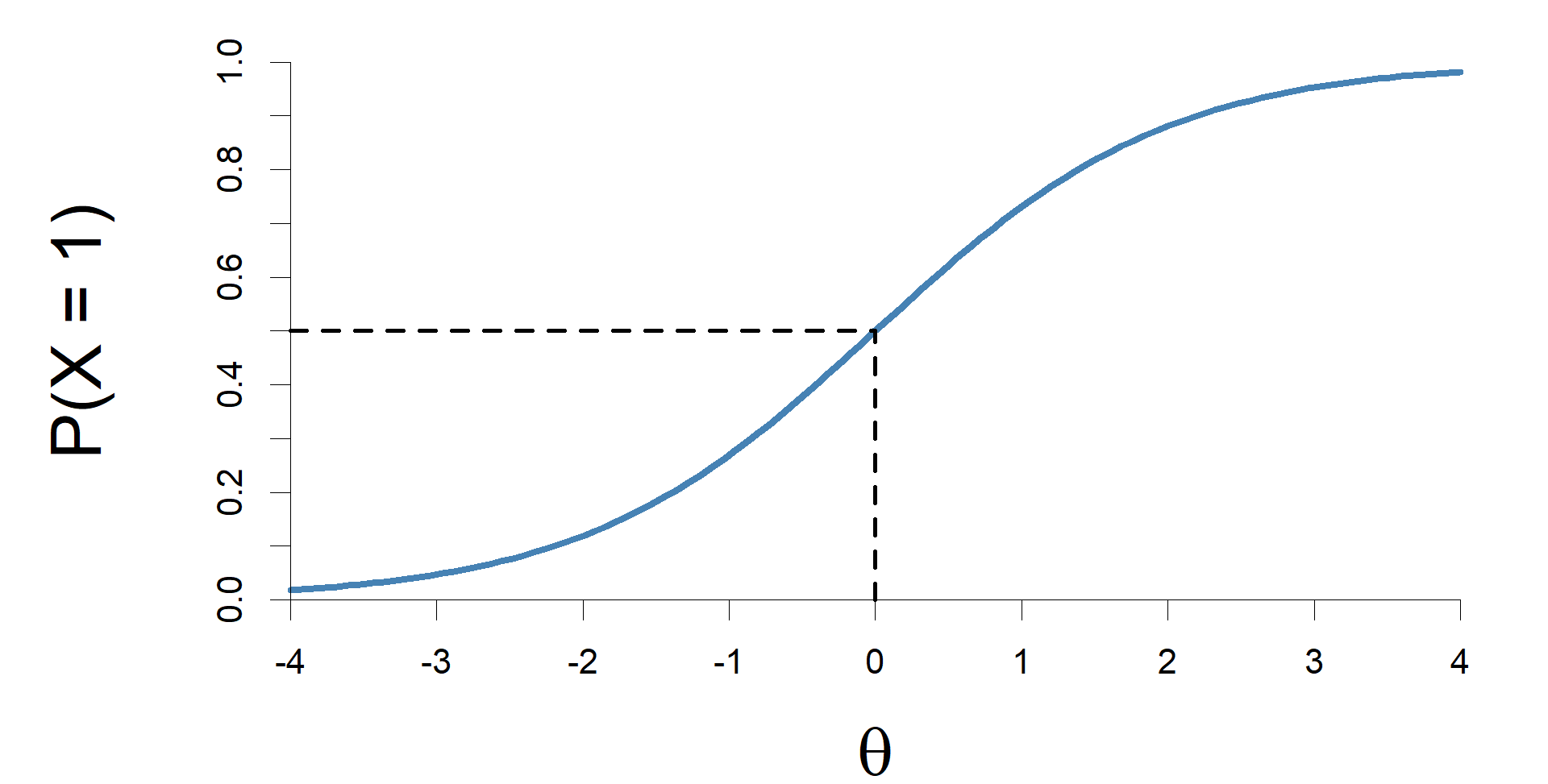
3. ábra. Az itemjelleggörbe egyparaméteres logisztikus modell esetén.

Fontos, hogy minél nagyobb a diszkriminációs paraméter értéke, annál nagyobb az item diszkriminációs képessége, vagyis annál inkább el tudja különíteni az item az alacsonyabb és magasabb képességgel rendelkező tesztkitöltőket, de ez csak az item képességtartománya körüli képességtartományban igaz, egyébként az item diszkriminációs képessége kisebb lehet, mint egy alacsonyabb diszkriminációs paraméterrel rendelkező item esetén. Az egy- és kétparaméteres logisztikus modellek feltételezik, hogy nagyon alacsony képességértékek esetén a helyes válasz valószínűsége nullához konvergál. Ez a feltevés azonban nem mindig tartható, mint például feleletválasztós teszteknél, ahol a helyes válasz valószínűsége számottevően eltérhet nullától még végtelenül alacsony képesség esetén is. A háromparaméteres logisztikus modell ezt a helyzetet modellezi a kétparaméteres logisztikus modell γi, úgynevezett találgatási (guessing) paraméterrel történő kiegészítésével.

\[P(x=1|\theta_p,\beta_i, \alpha_i, \gamma_i)=\gamma_i+(1-\gamma_i)\frac{e^{\alpha_i(\theta_p-\beta_i)}}{1+e^{\alpha_i(\theta_p-\beta_i)}}\]

A háromparaméteres logisztikus modell esetén jellemző itemjelleggörbe a 4. ábrán látható.

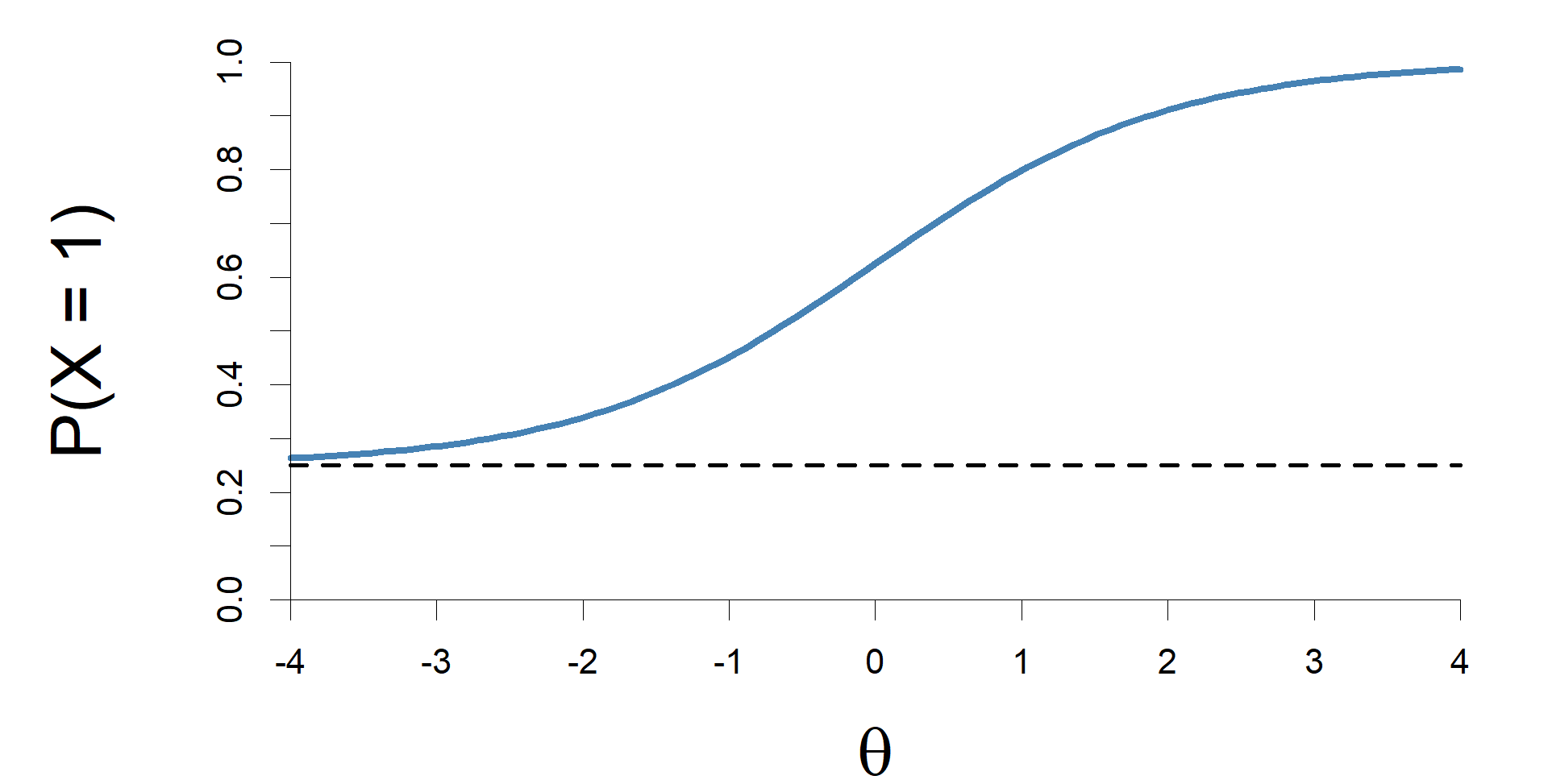
4. ábra Az itemjelleggörbe háromparaméteres logisztikus modell esetén, 0,25-ös találgatási paraméterrel.

4.2. Többértékű változók esetén alkalmazható IRT modellek

A fent leírt, dichotóm adatok esetén alkalmazható modellek mellett többértékű változók esetén alkalmazható modelleket is leírtak. Bár az IRT segítségével leggyakrabban dichotóm változókat vizsgáltak, gyakran előfordulnak olyan esetek, amikor például akkor is kaphat (rész)pontot a tesztkitöltő, amikor a válasz nem tökéletes, de részben jó. Másik példa lehet erre, amikor az itemeket egy (kettőnél több értékű) skálán mérjük, mint például a fentebb leírt depresszió skála esetén, amikor a tesztkitöltőnek négyfokú (0-3) skálán meg kell ítélnie, milyen gyakran tapasztalta az itemekben megfogalmazottakat.

Az ilyen típusú itemek elemzésére és értelmezésére irányuló igény nyomán több modellt is javasoltak. A legnépszerűbbek a Rating Scale Model (Andrich, 1978), a Partial Credit Model (Masters, 1982), és a Graded Response Model (GRM; Samejima, 1969), amelyek közül az utóbbit mutatjuk be röviden.

A GRM a 2PL egyfajta kiterjesztésének, általánosításának tekinthető többértékű, ordinális változókra. Az általánosítás mögöttes logikája a többértékű változók kétértékű változókká alakítása. Egy k válaszkategóriával rendelkező többértékű változó k-1 féleképpen alakítható kétértékűvé és az így dichotomizált változók esetén a kétparaméteres logisztikus modell alkalmazható:

\[P(x\geq k|\theta_p,\beta_{ik}, \alpha_i)=\frac{e^{\alpha_i(\theta_p-\beta_{ik})}}{1+e^{\alpha_i(\theta_p-\beta_{ik})}}\]

ahol k a k-ikválaszkategóriája, β_ik a k-ikküszöbérték, vagyis nehézségparaméter k-ik válaszkategóriára. Ilyen módon nem egy adott kategóriába eső válasz valószínűségét modellezük, hanem annak a valószínűségét, hogy a tesztkitöltő a k-ik vagy magasabb válaszkategóriát választ. Annak valószínűsége, hogy a a tesztkitöltő a k-ik kategóriát választja az alábbi módon számolható:

\[ P(x= k|\theta_p,\beta_{ik}, \alpha_i)=P(x\geq k|\theta_p,\beta_{ik}, \alpha_i)-P(x\geq k+1|\theta_p,\beta_{ik+1}, \alpha_i) \]

kivéve a legnagyobb válaszkategóriát, ahol:

\[ P(x= k|\theta_p,\beta_{ik}, \alpha_i)=P(x\geq k|\theta_p,\beta_{ik}, \alpha_i) \]