8 Varianciaelemzés
8.1 Egyszempontos varianciaelemzés
Az egyszempontos varianciaelemzés (independent one-way ANOVA) \(k\) független változó várható értékének egyezőségét vizsgálja. Az \(X_1, X_2, \dots, X_k\) változók mindegyike normális eloszlású és azonos \(\sigma\) szórással rendelkezik.
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0:\mu_1=\mu_2= \dots =\mu_k\)
- Ellenhipotézis:
- \(H_1:\) nem mindegyik várható érték egyenlő egymással
Alkalmazási feltételek:
- a \(X_1, X_2, \dots, X_k\) változók normális eloszlásúak
- a változók szórása megegyezik
Próbastatisztika:
A nullhipotézis igaz volta esetén az \(F\) próbastatisztika értéke \(F(k-1, N-k)\) eloszlást követ. A \(k\) a változók száma, \(N\) az összmintaelemszám:
\[F=\frac{\sum_{i=1}^kn_i(\bar{X_i}-\bar{X})^2/(k-1)}{\sum_{i=1}^k\sum_{j=1}^{n_i}(X_{i,j}-\bar{X_i})^2/(N-k)} \sim F(k-1, N-k)\]
8.1.1 Példa: az alkohol hatása a vezetési képességekre
Egy kísérletben 36 személy bevonásával az alkohol hatását vizsgálták a vezetési képességekre. A személyeket véletlenszerűen három csoportba sorolták, voltak akik alkoholmentes, alacsony alkoholtartalmú és a magas alkoholtartalmú italt fogyasztottak. Az alkoholmentes ital ugyanúgy nézett ki, és az íze is pontosan ugyanolyan volt, mint a többi italnak. A fogyasztott ital mennyissége a résztvevő testsúlya alapján lett meghatározva. A ital elfogyasztása után fél órával, a résztvevők 10 percig egy szimulátorban vezettek, amely nyilvántartotta az elkövetett hibák számát. Vizsgáljuk meg, hogy az elfogyasztott alkohol mennyisége milyen hatással van az elkövetett hibák számára!
Forrás: (Dancey and Reidy 2011, 303)
Adatok beolvasása. Olvassuk be az adatokat egy d nevű adattáblába. Az adatok széles szerkezetben állnak rendelkezésre, mivel mindhárom csoportban 12 személyt vizsgáltak. A széles adattáblát a reshape2 csomag melt() függvényével alakítjuk át a kívánt hosszú formátumba.
d <- read.table(file = textConnection("
placebo alacsony.alkohol magas.alkohol
5 5 8
10 7 10
7 9 8
3 8 9
5 2 11
7 5 15
11 6 7
2 6 11
3 4 8
5 4 8
6 8 17
6 10 11
"), header=T, sep="")
library(reshape2)
d.l <- melt(d, variable.name = "csoport", value.name = "hibak.szama", id.vars = NULL) # szélesből hosszú átalakítás
str(d.l) # az adattábla szerkezete## 'data.frame': 36 obs. of 2 variables:
## $ csoport : Factor w/ 3 levels "placebo","alacsony.alkohol",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ hibak.szama: int 5 10 7 3 5 7 11 2 3 5 ...d.l # a beolvasott adattábla## csoport hibak.szama
## 1 placebo 5
## 2 placebo 10
## 3 placebo 7
## 4 placebo 3
## 5 placebo 5
## 6 placebo 7
## 7 placebo 11
## 8 placebo 2
## 9 placebo 3
## 10 placebo 5
## 11 placebo 6
## 12 placebo 6
## 13 alacsony.alkohol 5
## 14 alacsony.alkohol 7
## 15 alacsony.alkohol 9
## 16 alacsony.alkohol 8
## 17 alacsony.alkohol 2
## 18 alacsony.alkohol 5
## 19 alacsony.alkohol 6
## 20 alacsony.alkohol 6
## 21 alacsony.alkohol 4
## 22 alacsony.alkohol 4
## 23 alacsony.alkohol 8
## 24 alacsony.alkohol 10
## 25 magas.alkohol 8
## 26 magas.alkohol 10
## 27 magas.alkohol 8
## 28 magas.alkohol 9
## 29 magas.alkohol 11
## 30 magas.alkohol 15
## 31 magas.alkohol 7
## 32 magas.alkohol 11
## 33 magas.alkohol 8
## 34 magas.alkohol 8
## 35 magas.alkohol 17
## 36 magas.alkohol 11Leíróstatisztikai mutatók. Első lépésként vizsgáljuk meg, hogy a legfontosabb leíró statisztikai mutatók a három csoportban hogyan alakulnak. Írassuk ki a 95%-os konfidenciaintervallum határait a csoportátlagokra.
library(psych)
psych::describeBy(x = d.l$hibak.szama, group = d.l$csoport, mat = T, digits = 3)## item group1 vars n mean sd median trimmed mad min max
## 11 1 placebo 1 12 5.833 2.691 5.5 5.7 2.224 2 11
## 12 2 alacsony.alkohol 1 12 6.167 2.329 6.0 6.2 2.965 2 10
## 13 3 magas.alkohol 1 12 10.250 3.049 9.5 9.9 2.224 7 17
## range skew kurtosis se
## 11 9 0.470 -0.833 0.777
## 12 8 -0.026 -1.152 0.672
## 13 10 0.982 -0.297 0.880library(DescTools); options(scipen = 8)
Desc(hibak.szama ~ csoport, data = d.l, digits = 3)## -------------------------------------------------------------------------
## hibak.szama ~ csoport
##
## Summary:
## n pairs: 36, valid: 36 (100.0%), missings: 0 (0.0%), groups: 3
##
##
## placebo alacsony.alkohol magas.alkohol
## mean 5.833 6.167 10.250
## median 5.500 6.000 9.500
## sd 2.691 2.329 3.049
## IQR 2.500 3.250 3.000
## n 12 12 12
## np 33.333% 33.333% 33.333%
## NAs 0 0 0
## 0s 0 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 13.77, df = 2, p-value = 0.001023library(DescTools)
aggregate(d.l$hibak.szama, list(d.l$csoport), MeanCI, conf.level = 0.95) # a 95%-os konfidenciaintervallum a csoportátlagokra## Group.1 x.mean x.lwr.ci x.upr.ci
## 1 placebo 5.833333 4.123442 7.543225
## 2 alacsony.alkohol 6.166667 4.686890 7.646443
## 3 magas.alkohol 10.250000 8.312856 12.187144Grafikus vizsgálatok. Az egyszempontos varianciaelemzéshez kapcsolódó első grafikus megjelenítés négy ábra megjelenítését teszi lehetővé. A PASWR2 csomag oneway.plots() függvénye egydimenziós pontdiagramot, két dobozdiagramot, és egy átlagdiagramot jelenít meg.
library(PASWR2)
oneway.plots(Y = d.l$hibak.szama, fac1 = d.l$csoport)
A yarrr csomag pirateplot() függvénye egyesíti a egydimenziós pontdiagram, a simított hisztogram és a csoportátlagokat reprezentáló oszlopdiagramok megjelenítését.
library(yarrr)
pirateplot(formula = hibak.szama ~ csoport, data = d.l, hdi.o = 0, line.o = 0, theme.o = 1, pal = "google")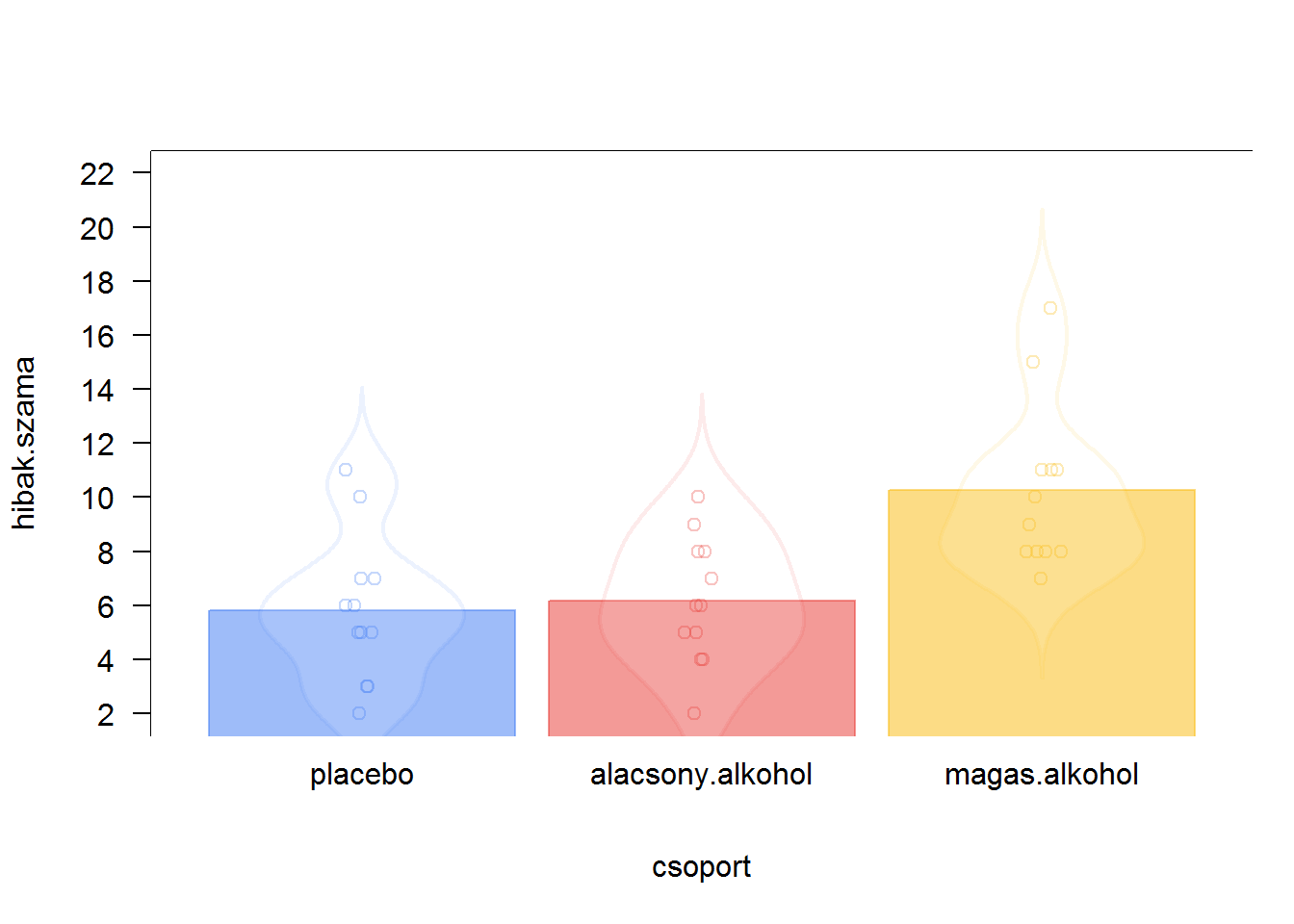
A gplots csomag plotmeans() függvényével átlagábrát hozhatunk létre a 95%-os konfidenciaintervallumokkal.
library(gplots)
plotmeans(formula = hibak.szama ~ csoport, data=d.l, xlab="Csoport", ylab="Hibák száma", p = 0.95)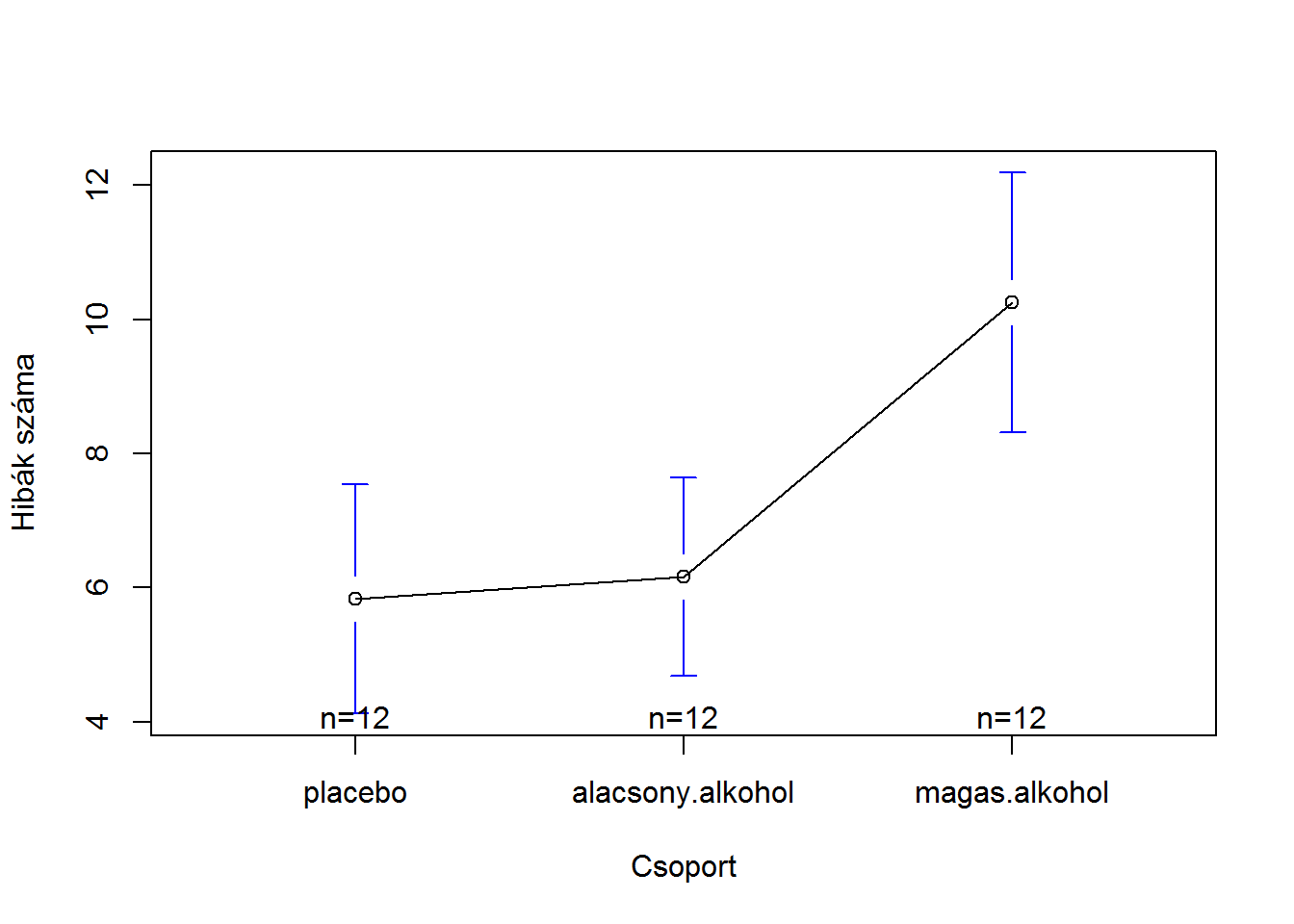
A fenti átlagábrát ggplot2 csomag segítségével is létrehozhatjuk.
library(ggplot2)
pic <- ggplot(data=d.l, aes(x=csoport, y=hibak.szama)) +
stat_summary(fun.data=mean_cl_normal, geom="line", size=1, aes(group=1)) +
stat_summary(fun.data=mean_cl_normal, geom="errorbar", size=1, width=0.1) +
stat_summary(fun.y=mean, geom="point", size=4, shape=21, fill="white") +
coord_cartesian(ylim = c(0, 16)) + theme_bw() + labs(x="Csoport", y="Hibák száma")
pic
Egyszempontos varianciaelemzés végrehajtása. Egyszempontos varianciaelemzés az aov() függvénnyel hajtható végre. A formula= argumentum a hibak.szama~csoport modell objektumot kapja értékül, ahol a függő változó a hibak.szama numerikus változó, a független változó a csoport faktor. A szokásos ANOVA táblázatot a summary() függvénnyel kapjuk meg.
aov.d <- aov(formula = hibak.szama ~ csoport, data = d.l) # egyszempontos varianciaelemzés
summary(aov.d) # ANOVA táblázat kiírása## Df Sum Sq Mean Sq F value Pr(>F)
## csoport 2 145.2 72.58 9.915 0.000425
## Residuals 33 241.6 7.32Az egyszempontos varianciaelemzés alapján azt mondhatjuk, hogy az alkoholfogyasztás különböző szintjein szignifikánsan eltér a hibázások átlagos száma, tehát az alkoholfogyasztás és a vezetési képességek kapcsolatban vannak (\(F(2,33)=9,915; p=0,0004\)).
Utóelemzések. Az ellenhipotézis teljesülése után végezzünk utóvizsgálatot.
Kezdjük a Bonferroni-féle páros összehasonlításokkal, amelyek a \(p\) értékek korrekciójával csökkentik az elsőfajú hibát. A pairwise.t.test() függvényben a p.adjust.method= argumentummal tudjuk beállítani a korrekció módját: Bonferroni-féle korrekció (nem szekvenciális Bonferroni) a p.adjust.method="bonferroni" argumentummal, Holm-féle korrekció (szekvenciális Bonferroni) a p.adjust.method="holm" argumentummal. Az összehasonlítások során használhatunk egy közös szórást (pool.sd=T) vagy páronként eltérő szórásokat (pool.sd=F).
## Páros összehasonlítások - Bonferroni
pairwise.t.test(x = d.l$hibak.szama, g = d.l$csoport, p.adjust.method = "bonferroni", pool.sd = F)##
## Pairwise comparisons using t tests with non-pooled SD
##
## data: d.l$hibak.szama and d.l$csoport
##
## placebo alacsony.alkohol
## alacsony.alkohol 1.0000 -
## magas.alkohol 0.0033 0.0042
##
## P value adjustment method: bonferroni## Páros összehasonlítások - Holm
pairwise.t.test(x = d.l$hibak.szama, g = d.l$csoport, p.adjust.method = "holm", pool.sd = F)##
## Pairwise comparisons using t tests with non-pooled SD
##
## data: d.l$hibak.szama and d.l$csoport
##
## placebo alacsony.alkohol
## alacsony.alkohol 0.7487 -
## magas.alkohol 0.0033 0.0033
##
## P value adjustment method: holmA fenti két outputból az utóbbi, kevésbé konzervatív szekvenciális Bonferroni próba eredményét értékeljük. A szekvenciális Bonferroni próba eredménye alapján azt mondhatjuk, hogy szignifikáns eltérés van a hibák számában a placebó és a magas alkohol csoportok, valamint az alacsony alkohol és magas alkohol csoportok között (mindkét esetben \(p=0,0033\)).
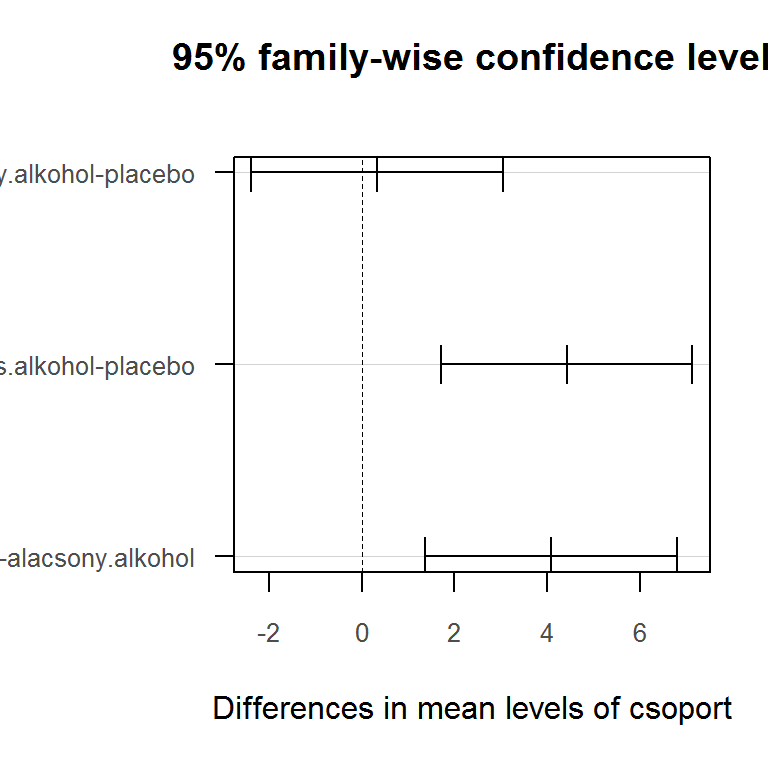
A páronkénti összehasonlításokat Scheffe-próba segítségével is elvégezhetjük. Használjuk a DescTools csomag ScheffeTest() függvényét.
library(DescTools)
ScheffeTest(x = d.l$hibak.szama, g = d.l$csoport, conf.level = 0.95) # Scheffe-próba##
## Posthoc multiple comparisons of means : Scheffe Test
## 95% family-wise confidence level
##
## $g
## diff lwr.ci upr.ci pval
## alacsony.alkohol-placebo 0.3333333 -2.497916 3.164583 0.9555
## magas.alkohol-placebo 4.4166667 1.585417 7.247916 0.0015 **
## magas.alkohol-alacsony.alkohol 4.0833333 1.252084 6.914583 0.0033 **
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1A Scheffe-próba eredménye alapján azt mondhatjuk, hogy szignifikáns eltérés van a hibák számában a placebó és a magas alkohol csoportok, valamint az alacsony alkohol és magas alkohol csoportok között (mindkét esetben \(p<0,0034\)).
A Tukey-próbával szintén össze tudunk hasonlítani minden csoportot minden egyéb csoporttal. A próba végrehajtására használhatjuk a multcomp csomag glht() függvényét. A model= argumentumban az egyszempontos varianciaelemzés modellobjektumát kell megadnunk, a linfct=mcp(csoport = "Tukey") argumentumban a független változó (csoport faktor) és a "Tukey" konstans megadására kell figyelnünk.
library(multcomp)
glht.1 <- glht(model = aov(hibak.szama ~ csoport, data = d.l), linfct = mcp(csoport = "Tukey")) # Tukey-próba
summary(glht.1) # a Tukey-próba eredménye##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = hibak.szama ~ csoport, data = d.l)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## alacsony.alkohol - placebo == 0 0.3333 1.1046 0.302 0.95112
## magas.alkohol - placebo == 0 4.4167 1.1046 3.998 0.00095
## magas.alkohol - alacsony.alkohol == 0 4.0833 1.1046 3.697 0.00217
## (Adjusted p values reported -- single-step method)confint(glht.1, level = 0.95) # 95%-os konfidenciaintervallumok ##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = hibak.szama ~ csoport, data = d.l)
##
## Quantile = 2.4548
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## alacsony.alkohol - placebo == 0 0.3333 -2.3782 3.0449
## magas.alkohol - placebo == 0 4.4167 1.7051 7.1282
## magas.alkohol - alacsony.alkohol == 0 4.0833 1.3718 6.7949par(mar=c(5.1, 11.1, 4.1, 2.1)); plot(glht.1) # 95%-os konfidenciaintervallumok ábrázolása
A Tukey-próba eredménye alapján azt mondhatjuk, hogy szignifikáns eltérés van a hibák számában a placebó és a magas alkohol csoportok, valamint az alacsony alkohol és magas alkohol csoportok között (mindkét esetben \(p<0,0023\)).
A Dunnett-próba egy referencia csoport és a többi csoport összehasonlítását végzi el. A referencia csoport a független változó (most csoport faktor) első szintje lesz. A glht függvényben a "Dunnett" konstanst kell használnunk.
library(multcomp)
glht.1 <- glht(model = aov(hibak.szama ~ csoport, data = d.l), linfct = mcp(csoport = "Dunnett")) # Dunnett próba
summary(glht.1) # a Tukey-próba eredménye##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = hibak.szama ~ csoport, data = d.l)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## alacsony.alkohol - placebo == 0 0.3333 1.1046 0.302 0.935827
## magas.alkohol - placebo == 0 4.4167 1.1046 3.998 0.000658
## (Adjusted p values reported -- single-step method)confint(glht.1, level = 0.95) # 95%-os konfidenciaintervallumok ##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = hibak.szama ~ csoport, data = d.l)
##
## Quantile = 2.3106
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## alacsony.alkohol - placebo == 0 0.3333 -2.2189 2.8856
## magas.alkohol - placebo == 0 4.4167 1.8644 6.9689par(mar=c(5.1, 11.1, 4.1, 2.1)); plot(glht.1) # 95%-os konfidenciaintervallumok ábrázolása
A Dunett-próba eredménye alapján azt mondhatjuk, hogy a placebó csoport csak a magas alkohol csoporttól tér el szignifikánsan (\(p<0,0007\)).
Tetszőleges két csoportot, vagy csoportok halmazát összehasonlíthatjuk kontrasztok segítségével. Az rbind() segítségével elkészítjük a kontraxmátrixot, amit a glht() függvényben kell megadnunk.
# kontraszt mátrix elkészítése
contr <- rbind("placebo ---- alkohol átlagosan" = c(2, -1, -1),
"placebo ---- alacsony alkohol" = c(1, -1, 0),
"placebo ---- magas alkohol" = c(1, 0, -1))
library(multcomp)
glht.1 <- glht(model = aov(hibak.szama ~ csoport, data = d.l), linfct = mcp(csoport = contr)) # kontraszt vizsgálat
summary(glht.1) # kontraszt vizsgálat eredménye##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = hibak.szama ~ csoport, data = d.l)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## placebo ---- alkohol átlagosan == 0 -4.7500 1.9132 -2.483 0.0368
## placebo ---- alacsony alkohol == 0 -0.3333 1.1046 -0.302 0.9370
## placebo ---- magas alkohol == 0 -4.4167 1.1046 -3.998 <0.001
## (Adjusted p values reported -- single-step method)confint(glht.1, level = 0.95) # 95%-os konfidenciaintervallumok ##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = hibak.szama ~ csoport, data = d.l)
##
## Quantile = 2.344
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## placebo ---- alkohol átlagosan == 0 -4.7500 -9.2346 -0.2654
## placebo ---- alacsony alkohol == 0 -0.3333 -2.9225 2.2559
## placebo ---- magas alkohol == 0 -4.4167 -7.0059 -1.8275par(mar=c(5.1, 11.1, 4.1, 2.1)); plot(glht.1) # 95%-os konfidenciaintervallumok ábrázolása
A fenti output három kontraszt vizsgálatának az eredményét tartalmazza. A placebó és az átlagos alkoholmérték összehasonlítása szignifikáns eredményt mutatat (\(p=0,0369\)), csakúgy, mint a placebó és a magas alkohol csoport (\(p<0,001\)).
Alkalmazási feltételek ellenőrzése. Először ellenőrizzük a szóráshomogenitási feltételt.
library(car)
leveneTest(y = hibak.szama ~ csoport, data = d.l, center = mean) # Levene-próba## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 2 0.2149 0.8078
## 33bartlett.test(formula = hibak.szama ~ csoport, data = d.l) # Bartlett-próba##
## Bartlett test of homogeneity of variances
##
## data: hibak.szama by csoport
## Bartlett's K-squared = 0.75872, df = 2, p-value = 0.6843A Levene-próba (\(F(2,33)=0,2148;p=0,8078\)) és a Bartlett-próba (\(\chi^2=0,7587;p=0,6843\)) is támogatja a szóráshomogenitási feltételt.
A normalitást ellenőrizzük a Shapiro–Wilk-próbával!
by(d.l$hibak.szama, d.l$csoport, shapiro.test) # Shapiro-Wilk-próba a három csoportban## d.l$csoport: placebo
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93564, p-value = 0.4437
##
## --------------------------------------------------------
## d.l$csoport: alacsony.alkohol
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97876, p-value = 0.9782
##
## --------------------------------------------------------
## d.l$csoport: magas.alkohol
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.84408, p-value = 0.03105# library(PASWR2)
# checking.plots(aov.d)A Shapiro–Wilk próba a placebó (\(p=0,4437\)) és az alacsony alkohol csoportban (\(p=0,9782\)) a normalitást támogatja, míg a magas alkohol csoportban a normalitási feltétel sérül (\(p=0,0311\)).
A hatás mértéke.
\(\eta^2\)
\(\omega^2\)
Alternatívák egyszempontos varianciaelemzésre. Egyszempontos varianciaelemzést a lessR csomag ANOVA() függvényével és a userfriendlyscience csomag oneway() függvényével is végrehajthatunk.
library(lessR)
ANOVA(my.formula = hibak.szama ~ csoport, data = d.l)

## BACKGROUND
##
## Response Variable: hibak.szama
##
## Factor Variable: csoport
## Levels: placebo alacsony.alkohol magas.alkohol
##
## Number of cases (rows) of data: 36
## Number of cases retained for analysis: 36
##
##
## DESCRIPTIVE STATISTICS
##
## n mean sd min max
## placebo 12 5.83 2.69 2.00 11.00
## alacsony.alkohol 12 6.17 2.33 2.00 10.00
## magas.alkohol 12 10.25 3.05 7.00 17.00
##
## Grand Mean: 7.417
##
##
## BASIC ANALYSIS
##
## df Sum Sq Mean Sq F-value p-value
## csoport 2 145.17 72.58 9.91 0.0004
## Residuals 33 241.58 7.32
##
##
## R Squared: 0.38
## R Sq Adjusted: 0.34
## Omega Squared: 0.33
##
## Cohen's f: 0.70
##
##
## Family-wise Confidence Level: 0.95
## ------------------------------------------------------
## diff lwr upr p adj
## alacsony.alkohol-placebo 0.33 -2.38 3.04 0.95
## magas.alkohol-placebo 4.42 1.71 7.13 0.00
## magas.alkohol-alacsony.alkohol 4.08 1.37 6.79 0.00
##
##
## RESIDUALS
##
## Fitted Values, Residuals, Standardized Residuals
## [sorted by Standardized Residuals, ignoring + or - sign]
## [res.rows = 20, out of 36 cases (rows) of data, or res.rows="all"]
## ---------------------------------------------------------
## csoport hibak.szama fitted residual z-resid
## 35 magas.alkohol 17 10.25 6.75 2.61
## 7 placebo 11 5.83 5.17 1.99
## 30 magas.alkohol 15 10.25 4.75 1.83
## 17 alacsony.alkohol 2 6.17 -4.17 -1.61
## 2 placebo 10 5.83 4.17 1.61
## 8 placebo 2 5.83 -3.83 -1.48
## 24 alacsony.alkohol 10 6.17 3.83 1.48
## 31 magas.alkohol 7 10.25 -3.25 -1.25
## 4 placebo 3 5.83 -2.83 -1.09
## 9 placebo 3 5.83 -2.83 -1.09
## 15 alacsony.alkohol 9 6.17 2.83 1.09
## 25 magas.alkohol 8 10.25 -2.25 -0.87
## 27 magas.alkohol 8 10.25 -2.25 -0.87
## 33 magas.alkohol 8 10.25 -2.25 -0.87
## 34 magas.alkohol 8 10.25 -2.25 -0.87
## 21 alacsony.alkohol 4 6.17 -2.17 -0.84
## 22 alacsony.alkohol 4 6.17 -2.17 -0.84
## 16 alacsony.alkohol 8 6.17 1.83 0.71
## 23 alacsony.alkohol 8 6.17 1.83 0.71
## 28 magas.alkohol 9 10.25 -1.25 -0.48
##
##
## ----------------------------------------
## Plot 1: Scatterplot with Cell Means
## Plot 2: 95% family-wise confidence level
## ----------------------------------------library(userfriendlyscience)
oneway(y = d.l$hibak.szama, x = d.l$csoport, levene = T, plot = T, posthoc = "games-howell")
## ### Oneway Anova for y=hibak.szama and x=csoport (groups: placebo, alacsony.alkohol, magas.alkohol)
##
## Eta Squared: 95% CI = [0.14; 0.52], point estimate = 0.38
##
## SS Df MS F p
## Between groups (error + effect) 145.17 2 72.58 9.91 <.001
## Within groups (error only) 241.58 33 7.32
##
## ### Levene's test:
##
## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 2 0.2149 0.8078
## 33
##
## ### Post hoc test: games-howell
##
## t df p
## placebo:alacsony.alkohol 0.32 21.56 .944
## placebo:magas.alkohol 3.76 21.67 .003
## alacsony.alkohol:magas.alkohol 3.69 20.58 .0048.2 Összetartozó mintás egyszempontos varianciaelemzés
Az összetartozó mintás egyszempontos varianciaelemzés (repeated-measures one-way ANOVA) tekinthető a páros t-próba általánosításának, amikor kettőnél több alkalomra vagy időpontra vonatkozó adatok állnak rendelkezésre. A próba nullhipotézise az egyes alkalmakkal mért \(k\) változók populációbeli várható értékének azonosságát állítja. Az alkalmazási feltételek között a normalitás és a szóráshomogenitásnak az összetartozó minták kapcsán megjelenő változata, a szfericitás szerepel.
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0:\mu_1=\mu_2= \dots =\mu_k\)
- Ellenhipotézis:
- \(H_1:\) nem mindegyik várható érték egyenlő egymással
Alkalmazási feltételek:
- a \(X_1, X_2, \dots, X_k\) változók normális eloszlásúak
- szfericitás (szórásegyezés)
8.2.1 Példa: az alkohol hatása a vezetési képességekre, összetartozó mintás eset.
Egy kísérletben 12 személy bevonásával az alkohol hatását vizsgálták a vezetési képességekre. A személyeket három alkalommal vizsgálták, három egymást követő hét hétfőjén. Először alkoholmentes, majd alacsony alkoholtartalmú és végül magas alkoholtartalmú italt fogyasztottak. Az alkoholmentes ital ugyanúgy nézett ki, és az íze is pontosan ugyanolyan volt, mint a többi italnak. A fogyasztott ital mennyissége a résztvevő testsúlya alapján lett meghatározva. A ital elfogyasztása után fél órával, a résztvevők 10 percig egy szimulátorban vezettek, amely nyilvántartotta az elkövetett hibák számát. Vizsgáljuk meg, hogy az elfogyasztott alkohol mennyisége milyen hatással van az elkövetett hibák számára!
Forrás: (Dancey and Reidy 2011, 313)
Adatok beolvasása. Olvassuk be az adatokat egy d nevű adattáblába:
d <- read.table(file = textConnection("
Participant placebo alacsony.alkohol magas.alkohol
1 5 5 8
2 10 7 10
3 7 9 8
4 3 8 9
5 5 2 11
6 7 5 15
7 11 6 7
8 2 6 11
9 3 4 8
10 5 4 8
11 6 8 17
12 6 10 11
"), header=T, sep="")
library(reshape2)
d.l <- melt(d, id.vars = "Participant", value.name = "hibak.szama", variable.name = "csoport") # szélesből-hosszú átalakítás
d.l$Participant <- factor(d$Participant)
str(d.l) # az adattábla szerkezete## 'data.frame': 36 obs. of 3 variables:
## $ Participant: Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## $ csoport : Factor w/ 3 levels "placebo","alacsony.alkohol",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ hibak.szama: int 5 10 7 3 5 7 11 2 3 5 ...d.l # a beolvasott adattábla## Participant csoport hibak.szama
## 1 1 placebo 5
## 2 2 placebo 10
## 3 3 placebo 7
## 4 4 placebo 3
## 5 5 placebo 5
## 6 6 placebo 7
## 7 7 placebo 11
## 8 8 placebo 2
## 9 9 placebo 3
## 10 10 placebo 5
## 11 11 placebo 6
## 12 12 placebo 6
## 13 1 alacsony.alkohol 5
## 14 2 alacsony.alkohol 7
## 15 3 alacsony.alkohol 9
## 16 4 alacsony.alkohol 8
## 17 5 alacsony.alkohol 2
## 18 6 alacsony.alkohol 5
## 19 7 alacsony.alkohol 6
## 20 8 alacsony.alkohol 6
## 21 9 alacsony.alkohol 4
## 22 10 alacsony.alkohol 4
## 23 11 alacsony.alkohol 8
## 24 12 alacsony.alkohol 10
## 25 1 magas.alkohol 8
## 26 2 magas.alkohol 10
## 27 3 magas.alkohol 8
## 28 4 magas.alkohol 9
## 29 5 magas.alkohol 11
## 30 6 magas.alkohol 15
## 31 7 magas.alkohol 7
## 32 8 magas.alkohol 11
## 33 9 magas.alkohol 8
## 34 10 magas.alkohol 8
## 35 11 magas.alkohol 17
## 36 12 magas.alkohol 11Leíróstatisztikai mutatók.
library(psych)
psych::describeBy(x = d.l$hibak.szama, group = d.l$csoport, mat = T)## item group1 vars n mean sd median trimmed mad
## 11 1 placebo 1 12 5.833333 2.691175 5.5 5.7 2.2239
## 12 2 alacsony.alkohol 1 12 6.166667 2.329000 6.0 6.2 2.9652
## 13 3 magas.alkohol 1 12 10.250000 3.048845 9.5 9.9 2.2239
## min max range skew kurtosis se
## 11 2 11 9 0.46983633 -0.8330127 0.7768754
## 12 2 10 8 -0.02565285 -1.1515253 0.6723245
## 13 7 17 10 0.98247561 -0.2971578 0.8801257library(DescTools)
Desc(hibak.szama ~ csoport, data = d.l)## -------------------------------------------------------------------------
## hibak.szama ~ csoport
##
## Summary:
## n pairs: 36, valid: 36 (100.0%), missings: 0 (0.0%), groups: 3
##
##
## placebo alacsony.alkohol magas.alkohol
## mean 5.8333333 6.1666667 10.2500000
## median 5.5000000 6.0000000 9.5000000
## sd 2.6911753 2.3290003 3.0488448
## IQR 2.5000000 3.2500000 3.0000000
## n 12 12 12
## np 33.3333333% 33.3333333% 33.3333333%
## NAs 0 0 0
## 0s 0 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 13.77, df = 2, p-value = 0.001023Grafikus vizsgálatok.
library(PASWR2)
oneway.plots(Y = d.l$hibak.szama, fac1 = d.l$csoport)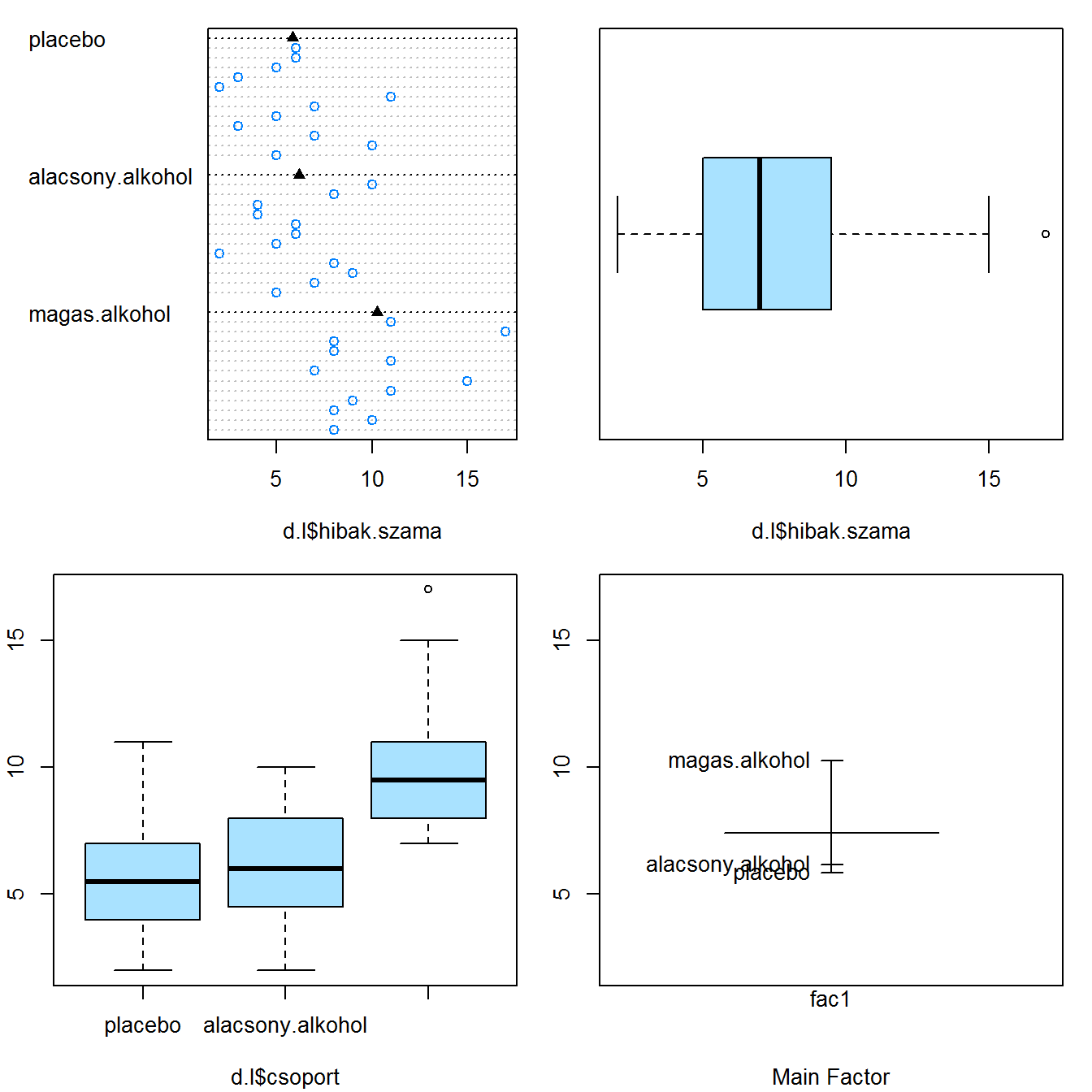
library(yarrr)
pirateplot(formula = hibak.szama ~ csoport, data = d.l, hdi.o = 0, line.o = 0, theme.o = 1, pal = "google")
library(gplots)
plotmeans(formula = hibak.szama ~ csoport, data=d.l, xlab="Csoport", ylab="Hibák száma", main="Mean Plot\nwith 95% CI")
library(ggplot2)
pic <- ggplot(data=d.l, aes(x=csoport, y=hibak.szama)) +
stat_summary(fun.data=mean_cl_normal, geom="line", size=1, aes(group=1)) +
stat_summary(fun.data=mean_cl_normal, geom="errorbar", size=1, width=0.1) +
stat_summary(fun.y=mean, geom="point", size=4, shape=21, fill="white") +
coord_cartesian(ylim = c(0, 16)) + theme_bw() + labs(x="Csoport", y="Hibák száma")
pic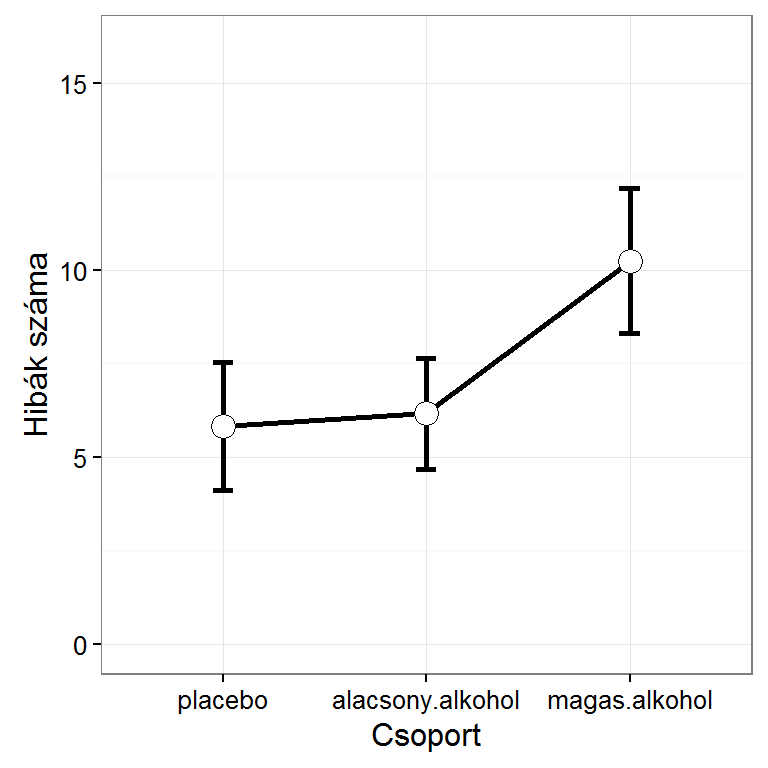
Egyszempontos összetartozó mintás varianciaelemzés végrehajtása. *Egyszempontos összetartozó mintás varianciaelemzés végrehajtható az aov() függvénnyel és az ez csomag ezANOVA() függvényével is. Az aov() függvény hívása során az összetartozó minták miatt szükség van az Error() tagra is, amely tartalmazza a személyek azonosító változó nevét (Participant) és a személyen belüli faktor változót (csoport).
Az ezANOVA() függvény részletesebb outputtal rendelkezik, például Mauchly-próbát is végez a szfericitás ellenőrzésére. A füügvény hívása során meg kell adnunk a függő változó nevét (dv=hibak.szama), a személyek azonosító változóját (wid=Participant) és a személyen belüli faktort (within=csoport). A detailed=T argumentummal részletes outputot kérünk.
aov.d <- aov(hibak.szama ~ csoport + Error(Participant/csoport), data = d.l)
summary(aov.d)##
## Error: Participant
## Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 11 94.08 8.553
##
## Error: Participant:csoport
## Df Sum Sq Mean Sq F value Pr(>F)
## csoport 2 145.2 72.58 10.83 0.000533
## Residuals 22 147.5 6.70library(ez)
ezANOVA(data = d.l, dv = hibak.szama, wid = Participant, within = csoport, detailed = T)## $ANOVA
## Effect DFn DFd SSn SSd F p
## 1 (Intercept) 1 11 1980.2500 94.08333 231.52613 0.000000009803446
## 2 csoport 2 22 145.1667 147.50000 10.82599 0.000532851693527
## p<.05 ges
## 1 * 0.8912685
## 2 * 0.3753501
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 2 csoport 0.9089291 0.620369
##
## $`Sphericity Corrections`
## Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05
## 2 csoport 0.9165307 0.0008189724 * 1.090699 0.0005328517 *A fenti outputból kiolvasható, hogy a szfericitási feltétel teljesül (Mauchly-próba: \(W=0,9089; p=0,6204\)), így az egyszempontos összetartozó mintás varianciaelemzés feltétele teljesül. (Megjegyezzük, hogy amennyiben a Mauchly-próba szignifikáns, akkor a szfericitási feltétel hiányban a p[GG] Greenhouse-Geisser vagy a p[HF] Huynh-Feldt korrigált \(p\) értékek nyújtanak tájékozódást az egyszempontos összetartozó mintás varianciaelemzés nullhipotéziséről.)
Az egyszempontos összetartozó mintás varianciaelemzés eredménye szignifikáns (\(F(2, 22)=10,83; p=0,0005\)), vagyis az alkoholfogyasztás mértéke szignigikánsan befolyásolja a vezetési képességet.
Utóelemzések. Végezzünk utóelemzést nem szekvenciális Bonferroni próbával! A pairwise.t.test() függvényben a p.adjust.method= argumentummmal tudjuk beállítani a korrekció módját, Bonferroni-féle korrekció (nem szekvenciális Bonferroni) esetén a p.adjust.method="bonferroni" argumentummal. Összetartozó mintás eset lévén hasznlnunk kell a paired=T argumentumot is.
pairwise.t.test(x = d.l$hibak.szama, g = d.l$csoport, paired = T, p.adjust.method = "bonferroni")##
## Pairwise comparisons using paired t tests
##
## data: d.l$hibak.szama and d.l$csoport
##
## placebo alacsony.alkohol
## alacsony.alkohol 1.0000 -
## magas.alkohol 0.0107 0.0068
##
## P value adjustment method: bonferroniA nem szekvenciális Bonferroni próba eredménye alapján azt mondhatjuk, hogy szignifikáns eltérés van a hibák számában a placebó és a magas alkohol csoportok, valamint az alacsony alkohol és magas alkohol csoportok között (mindkét esetben \(p<0,011\)).
library(DescTools)
EtaSq(aov.d, type=1)## eta.sq eta.sq.part eta.sq.gen
## csoport 0.3753501 0.4960137 0.37535018.3 Többszempontos varianciaelemzés
A többszempontos varianciaelemzés (independent multi-factorial ANOVA) több független faktort hatását vizsgálja a folytonos függő változóra.
A kétszempontos és a háromszempontos (háromfaktoros) varianciaelemzés lineáris modellje:
\[y_{ijk}=\mu+\alpha_i+\beta_j+(\alpha \beta)_{ij} + \varepsilon_{ijk}\]
\[y_{ijkl}=\mu+\alpha_i+\beta_j+\gamma_k+(\alpha \beta)_{ij} + (\alpha \gamma)_{ik} + (\beta \gamma)_{jk} + (\alpha \beta \gamma)_{ijk} + \varepsilon_{ijkl}\]
A fenti egyenletekben a \(\mu\) az összátlag, az \(\alpha\) az \(A\) faktor hatása, a \(\beta\) a \(B\) faktor hatása és a \(\gamma\) a \(C\) faktor hatása. A továbbiakban a kétszempontos varianciaelemzés modelljét tárgyaljuk. Az \(A\) faktor rendelkezzen \(I\), a \(B\) faktor pedig \(J\) különböző szinttel.
Null- és ellenhipotézisek:
- az \((A \times B)\) interakcióra
- Nullhipotézis:
- \(H_0:(\alpha \beta)_{11}=(\alpha \beta)_{12}= \dots =(\alpha \beta)_{IJ}=0\)
vagy
- \(H_0:\) nincs \((A \times B)\) interakció
- \(H_0:(\alpha \beta)_{11}=(\alpha \beta)_{12}= \dots =(\alpha \beta)_{IJ}=0\)
- Ellenhipotézis:
- \(H_1:(\alpha \beta)_{ij} \neq 0\) legalább egy \((\alpha \beta)_{ij}\)-re
vagy
- \(H_1:\) van \((A \times B)\) interakció
- \(H_1:(\alpha \beta)_{ij} \neq 0\) legalább egy \((\alpha \beta)_{ij}\)-re
- Nullhipotézis:
- az \(A\) faktorra
- Nullhipotézis:
- \(H_0:\mu(A)_1=\mu(A)_2= \dots =\mu(A)_I\)
vagy
- \(H_0:\alpha_1=\alpha_2= \dots =\alpha_I=0\)
vagy
- \(H_0:\) az \(A\) faktornak nincs hatása
- \(H_0:\mu(A)_1=\mu(A)_2= \dots =\mu(A)_I\)
- Ellenhipotézis:
- \(H_1:\) nem mindegyik \(I\) db várható érték egyenlő egymással
vagy
- \(H_1:\alpha_i \neq 0\) legalább egy \(\alpha_i\)-re
vagy
- \(H_1:\) az \(A\) faktornak van hatása
- \(H_1:\) nem mindegyik \(I\) db várható érték egyenlő egymással
- Nullhipotézis:
- a \(B\) faktorra
- Nullhipotézis:
- \(H_0:\mu(B)_1=\mu(B)_2= \dots =\mu(B)_J\)
vagy
- \(H_0:\beta_1=\beta_2= \dots =\beta_J=0\)
vagy
- \(H_0:\) a \(B\) faktornak nincs hatása
- \(H_0:\mu(B)_1=\mu(B)_2= \dots =\mu(B)_J\)
- Ellenhipotézis:
- \(H_1:\) nem mindegyik \(J\) db várható érték egyenlő egymással
vagy
- \(H_1:\beta_j \neq 0\) legalább egy \(\beta_j\)-re
vagy
- \(H_1:\) a \(B\) faktornak van hatása
- \(H_1:\) nem mindegyik \(J\) db várható érték egyenlő egymással
- Nullhipotézis:
Alkalmazási feltételek:
- független minták
- normalitás
- szóráshomogenitás
8.3.1 Példa: antidepresszánsok hatása.
Egy vizsgálatban antidepresszánsok hatását vizsgálták. A kísérlet 18 résztvevőjét 3 csoportba sorolták a kapott gyógyszer szerint. A kontrollcsoport placebót kapott, a másik két csoport Anxifree, valamint Joyzepam nevű antidepresszánst kapott. Mindegyik csoportban voltak olyanok, akiknek a gyógyulását kognitív viselkedésterápiával segítették. Az antidepresszánsok hatását a 3 hónapos kezelés után a hangulati állapotban bekövetkező változás segítségével mérjük (\(\left[-5,5\right]\) közötti skálán). Vizsgáljuk meg, hogy milyen az antidepresszánsok hatása!
Forrás: Daniel Navarro (2015). Learning statistics with R: A tutorial for psychology students and other beginners (Version 0.5)
Adatok beolvasása. Olvassuk be az adatokat egy d nevű adattáblába:
d <- read.table(file = textConnection("
drug therapy mood.gain
placebo no.therapy 0.5
placebo no.therapy 0.3
placebo no.therapy 0.1
anxifree no.therapy 0.6
anxifree no.therapy 0.4
anxifree no.therapy 0.2
joyzepam no.therapy 1.4
joyzepam no.therapy 1.7
joyzepam no.therapy 1.3
placebo CBT 0.6
placebo CBT 0.9
placebo CBT 0.3
anxifree CBT 1.1
anxifree CBT 0.8
anxifree CBT 1.2
joyzepam CBT 1.8
joyzepam CBT 1.3
joyzepam CBT 1.4
"), header=T, sep="")
d$drug <- factor(d$drug, levels=c("placebo", "anxifree", "joyzepam"))
d$therapy <- factor(d$therapy, levels=c("no.therapy", "CBT"))
str(d) # az adattábla szerkezete## 'data.frame': 18 obs. of 3 variables:
## $ drug : Factor w/ 3 levels "placebo","anxifree",..: 1 1 1 2 2 2 3 3 3 1 ...
## $ therapy : Factor w/ 2 levels "no.therapy","CBT": 1 1 1 1 1 1 1 1 1 2 ...
## $ mood.gain: num 0.5 0.3 0.1 0.6 0.4 0.2 1.4 1.7 1.3 0.6 ...d # a beolvasott adattábla## drug therapy mood.gain
## 1 placebo no.therapy 0.5
## 2 placebo no.therapy 0.3
## 3 placebo no.therapy 0.1
## 4 anxifree no.therapy 0.6
## 5 anxifree no.therapy 0.4
## 6 anxifree no.therapy 0.2
## 7 joyzepam no.therapy 1.4
## 8 joyzepam no.therapy 1.7
## 9 joyzepam no.therapy 1.3
## 10 placebo CBT 0.6
## 11 placebo CBT 0.9
## 12 placebo CBT 0.3
## 13 anxifree CBT 1.1
## 14 anxifree CBT 0.8
## 15 anxifree CBT 1.2
## 16 joyzepam CBT 1.8
## 17 joyzepam CBT 1.3
## 18 joyzepam CBT 1.4Leíróstatisztikai mutatók. A drug faktor 3 szinttel, a therapy faktor 2 szinttel rendelkezik, így összesen 6 csoportunk van. Határozzuk meg a tapply() függvénnyel ezekben a csoportokban az átlagokat, szórásokat és a csoportok mintaelemszámát!
tapply(d$mood.gain, d[,c("drug", "therapy")], mean, na.rm = T) # átlagok## therapy
## drug no.therapy CBT
## placebo 0.300000 0.600000
## anxifree 0.400000 1.033333
## joyzepam 1.466667 1.500000tapply(d$mood.gain, d[,c("drug", "therapy")], sd, na.rm = T) # szórások## therapy
## drug no.therapy CBT
## placebo 0.2000000 0.3000000
## anxifree 0.2000000 0.2081666
## joyzepam 0.2081666 0.2645751tapply(d$mood.gain, d[,c("drug", "therapy")], function(x) sum(!is.na(x))) # csoportok elemszáma## therapy
## drug no.therapy CBT
## placebo 3 3
## anxifree 3 3
## joyzepam 3 3Grafikus vizsgálatok. A PASWR2 csomag twoway.plots() függvénye alkalmas a kétszempontos varianciaelemzés grafikus megjelenítésére. Az első két ábrán a két faktor dobozdiagramját kapjuk, majd két átlagábrát tanulmányozhatunk.
library(PASWR2)
twoway.plots(Y = d$mood.gain, fac1 = d$drug, fac2 = d$therapy)
Kétszempontos varianciaelemzés végrehajtása. Az aov() függvényben az interakciót is tartalmazó modellt adjuk meg (formula=mood.gain~drug*therapy), majd a summary() függvénnyel kérjük le az ANOVA táblázatot.
aov.d <- aov(formula = mood.gain ~ drug * therapy, data = d)
summary(aov.d)## Df Sum Sq Mean Sq F value Pr(>F)
## drug 2 3.453 1.7267 31.714 0.0000162
## therapy 1 0.467 0.4672 8.582 0.0126
## drug:therapy 2 0.271 0.1356 2.490 0.1246
## Residuals 12 0.653 0.0544A kétszempontos varianciaelemzés alapján megállapíthatjuk, hogy mindkét főhatás szignifikáns, a gyógyszeres kezelésnek (\(F(2, 12)=31,71; p<0,0001\)) és a terápiának (\(F(1, 12)=8,58; p=0,0126\)) is van hatása. Az interakció a két faktor között nem szignifikáns (\(F(2, 12)=2,49; p=0,1246\)).
Utóelemzések. Fennt megállapítottuk, hogy mindkét faktor hatása szignifikáns, most nézzük meg ezeket a hatásokat részletesen Tukey-próbával. Mindkét faktorra külön-külön páronkénti összehasonlításokkal megvizsgáljuk, hogy mely csoportok között van szignifikáns különbség. Használhatjuk a multcomp csomag glht() függvényét és a TukeyHSD() függvényt is.
library(multcomp)
glht.1 <- glht(model = aov(mood.gain ~ drug + therapy, data = d), linfct = mcp(drug = "Tukey")) # Tukey-próba
summary(glht.1) # a Tukey-próba eredménye##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = mood.gain ~ drug + therapy, data = d)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## anxifree - placebo == 0 0.2667 0.1484 1.797 0.206
## joyzepam - placebo == 0 1.0333 0.1484 6.965 <0.001
## joyzepam - anxifree == 0 0.7667 0.1484 5.168 <0.001
## (Adjusted p values reported -- single-step method)confint(glht.1, level = 0.95) # 95%-os konfidenciaintervallumok ##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = mood.gain ~ drug + therapy, data = d)
##
## Quantile = 2.6165
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## anxifree - placebo == 0 0.2667 -0.1215 0.6548
## joyzepam - placebo == 0 1.0333 0.6452 1.4215
## joyzepam - anxifree == 0 0.7667 0.3785 1.1548par(mar=c(5.1, 9.1, 4.1, 2.1)); plot(glht.1) # 95%-os konfidenciaintervallumok ábrázolása
library(multcomp)
glht.1 <- glht(model = aov(mood.gain ~ drug + therapy, data = d), linfct = mcp(therapy = "Tukey")) # Tukey-próba
summary(glht.1) # a Tukey-próba eredménye##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = mood.gain ~ drug + therapy, data = d)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## CBT - no.therapy == 0 0.3222 0.1211 2.66 0.0187
## (Adjusted p values reported -- single-step method)confint(glht.1, level = 0.95) # 95%-os konfidenciaintervallumok ##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = mood.gain ~ drug + therapy, data = d)
##
## Quantile = 2.1448
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## CBT - no.therapy == 0 0.32222 0.06241 0.58203par(mar=c(5.1, 9.1, 4.1, 2.1)); plot(glht.1) # 95%-os konfidenciaintervallumok ábrázolása
A fenti sorok helyett használhatjuk a TukeyHSD() függvényt is, az eredmény az előzőekkel megegyező lesz.
TukeyHSD(aov(mood.gain ~ drug + therapy, data = d))## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = mood.gain ~ drug + therapy, data = d)
##
## $drug
## diff lwr upr p adj
## anxifree-placebo 0.2666667 -0.1216321 0.6549655 0.2062942
## joyzepam-placebo 1.0333333 0.6450345 1.4216321 0.0000186
## joyzepam-anxifree 0.7666667 0.3783679 1.1549655 0.0003934
##
## $therapy
## diff lwr upr p adj
## CBT-no.therapy 0.3222222 0.0624132 0.5820312 0.0186602A Tukey-próba eredménye alapján a Joyzepam antidepresszánssal szignifikánsan jobb eredményt érhetünk el, mint a placebóval, vagy a korábban használt Anxifree-vel (mindkét esetben \(p<0,0004\)).
Alternatívák kétszempontos varianciaelemzésre. Használjuk a lessR csomag ANOVA() függvényét!
library(lessR)
ANOVA(my.formula = mood.gain ~ drug * therapy, data = d)
## BACKGROUND
##
## Response Variable: mood.gain
##
## Factor Variable 1: drug
## Levels: placebo anxifree joyzepam
##
## Factor Variable 2: therapy
## Levels: no.therapy CBT
##
## Number of cases (rows) of data: 18
## Number of cases retained for analysis: 18
##
## The design is balanced
##
## Two-way Between Groups ANOVA
##
##
## DESCRIPTIVE STATISTICS
##
## Cell Sample Size: 3
##
##
## drug
## therapy placebo anxifree joyzepam
## no.therapy 0.30 0.40 1.47
## CBT 0.60 1.03 1.50
##
##
## drug
## -----------------------------
## placebo anxifree joyzepam
## 1 0.45 0.72 1.48
##
## therapy
## -------------------
## no.therapy CBT
## 1 0.72 1.04
##
##
## 0.883
##
##
## drug
## therapy placebo anxifree joyzepam
## no.therapy 0.20 0.20 0.21
## CBT 0.30 0.21 0.26
##
##
## BASIC ANALYSIS
##
## df Sum Sq Mean Sq F-value p-value
## drug 2 3.45 1.73 31.71 0.0000
## therapy 1 0.47 0.47 8.58 0.0126
## drug:therapy 2 0.27 0.14 2.49 0.1246
## Residuals 12 0.65 0.05
##
##
## Partial Omega Squared for drug: 0.77
## Partial Omega Squared for therapy: 0.30
## Partial Omega Squared for drug & therapy: 0.14
##
## Cohen's f for drug: 1.85
## Cohen's f for therapy: 0.65
## Cohen's f for drug_&_therapy: 0.41
##
##
##
## Family-wise Confidence Level: 0.95
##
## Factor: drug
## -----------------------------------------
## diff lwr upr p adj
## anxifree-placebo 0.27 -0.09 0.63 0.16
## joyzepam-placebo 1.03 0.67 1.39 0.00
## joyzepam-anxifree 0.77 0.41 1.13 0.00
##
## Factor: therapy
## -------------------------------------
## diff lwr upr p adj
## CBT-no.therapy 0.32 0.08 0.56 0.01
##
## Cell Means
## -----------------------------------------------------------------
## diff lwr upr p adj
## anxifree:no.therapy-placebo:no.therapy 0.10 -0.54 0.74 0.99
## joyzepam:no.therapy-placebo:no.therapy 1.17 0.53 1.81 0.00
## placebo:CBT-placebo:no.therapy 0.30 -0.34 0.94 0.63
## anxifree:CBT-placebo:no.therapy 0.73 0.09 1.37 0.02
## joyzepam:CBT-placebo:no.therapy 1.20 0.56 1.84 0.00
## joyzepam:no.therapy-anxifree:no.therapy 1.07 0.43 1.71 0.00
## placebo:CBT-anxifree:no.therapy 0.20 -0.44 0.84 0.89
## anxifree:CBT-anxifree:no.therapy 0.63 -0.01 1.27 0.05
## joyzepam:CBT-anxifree:no.therapy 1.10 0.46 1.74 0.00
## placebo:CBT-joyzepam:no.therapy -0.87 -1.51 -0.23 0.01
## anxifree:CBT-joyzepam:no.therapy -0.43 -1.07 0.21 0.28
## joyzepam:CBT-joyzepam:no.therapy 0.03 -0.61 0.67 1.00
## anxifree:CBT-placebo:CBT 0.43 -0.21 1.07 0.28
## joyzepam:CBT-placebo:CBT 0.90 0.26 1.54 0.01
## joyzepam:CBT-anxifree:CBT 0.47 -0.17 1.11 0.21
##
##
## RESIDUALS
##
## Fitted Values, Residuals, Standardized Residuals
## [sorted by Standardized Residuals, ignoring + or - sign]
## [res.rows = 18, out of 18 ]
## ----------------------------------------------------------
## drug therapy mood.gain fitted residual z-resid
## 11 placebo CBT 0.90 0.60 0.30 1.57
## 16 joyzepam CBT 1.80 1.50 0.30 1.57
## 12 placebo CBT 0.30 0.60 -0.30 -1.57
## 8 joyzepam no.therapy 1.70 1.47 0.23 1.22
## 14 anxifree CBT 0.80 1.03 -0.23 -1.22
## 3 placebo no.therapy 0.10 0.30 -0.20 -1.05
## 1 placebo no.therapy 0.50 0.30 0.20 1.05
## 6 anxifree no.therapy 0.20 0.40 -0.20 -1.05
## 17 joyzepam CBT 1.30 1.50 -0.20 -1.05
## 4 anxifree no.therapy 0.60 0.40 0.20 1.05
## 15 anxifree CBT 1.20 1.03 0.17 0.87
## 9 joyzepam no.therapy 1.30 1.47 -0.17 -0.87
## 18 joyzepam CBT 1.40 1.50 -0.10 -0.52
## 13 anxifree CBT 1.10 1.03 0.07 0.35
## 7 joyzepam no.therapy 1.40 1.47 -0.07 -0.35
## 2 placebo no.therapy 0.30 0.30 -0.00 0.00
## 5 anxifree no.therapy 0.40 0.40 0.00 0.00
## 10 placebo CBT 0.60 0.60 -0.00 0.008.3.2 Példa: a mobiltelefon használatának hatása a vezetésre.
Egy kísérletben azt vizsgáljuk, hogy a vezetés közbeni telefonhasználat hogyan hat az elkövetett hibák számára. A függő változó tehát a szimulátorban elkövetett hibák száma volt. A vizsgálati személyeket 3 csoportba soroltuk: a kontrolcsoportban nem volt telefonhasználat, míg a másik kettőben különböző igénybevételű beszélgetést kellett folytatni fejhallgatón keresztül. Az Egyszerű csoportban csak a hallott szavakat kellett megismételni, a Bonyolult csoportban a hallott szó utolsó betűjével kellet egy új szót mondani. Az egyes csoportokban a kísérleti személyek további 2-2 alcsoportba sorolhatók. Az egyik alcsoportban könnyebb, míg a másikban nehezebb vezetési feladatott kellett megoldani. Vizsgáljuk meg, hogy a telefonálás hatását a vezetésre!
Forrás: Andrew Conway: Statistics One, Lecture 17: Factorial ANOVA (https://www.coursera.org/course/stats1)
Adatok beolvasása. Olvassuk be az adatokat egy d nevű adattáblába:
d <- read.table(file = textConnection('
"subject" "beszelgetes" "vezetes" "hibak.szama"
"1" 1 "Nem volt" "Könnyű" 20
"2" 2 "Nem volt" "Könnyű" 19
"3" 3 "Nem volt" "Könnyű" 31
"4" 4 "Nem volt" "Könnyű" 27
"5" 5 "Nem volt" "Könnyű" 31
"6" 6 "Nem volt" "Könnyű" 17
"7" 7 "Nem volt" "Könnyű" 23
"8" 8 "Nem volt" "Könnyű" 26
"9" 9 "Nem volt" "Könnyű" 11
"10" 10 "Nem volt" "Könnyű" 15
"11" 11 "Nem volt" "Könnyű" 13
"12" 12 "Nem volt" "Könnyű" 18
"13" 13 "Nem volt" "Könnyű" 21
"14" 14 "Nem volt" "Könnyű" 13
"15" 15 "Nem volt" "Könnyű" 13
"16" 16 "Nem volt" "Könnyű" 14
"17" 17 "Nem volt" "Könnyű" 20
"18" 18 "Nem volt" "Könnyű" 26
"19" 19 "Nem volt" "Könnyű" 20
"20" 20 "Nem volt" "Könnyű" 14
"21" 21 "Nem volt" "Nehéz" 10
"22" 22 "Nem volt" "Nehéz" 23
"23" 23 "Nem volt" "Nehéz" 31
"24" 24 "Nem volt" "Nehéz" 32
"25" 25 "Nem volt" "Nehéz" 24
"26" 26 "Nem volt" "Nehéz" 26
"27" 27 "Nem volt" "Nehéz" 46
"28" 28 "Nem volt" "Nehéz" 25
"29" 29 "Nem volt" "Nehéz" 23
"30" 30 "Nem volt" "Nehéz" 25
"31" 31 "Nem volt" "Nehéz" 13
"32" 32 "Nem volt" "Nehéz" 32
"33" 33 "Nem volt" "Nehéz" 32
"34" 34 "Nem volt" "Nehéz" 16
"35" 35 "Nem volt" "Nehéz" 26
"36" 36 "Nem volt" "Nehéz" 24
"37" 37 "Nem volt" "Nehéz" 11
"38" 38 "Nem volt" "Nehéz" 15
"39" 39 "Nem volt" "Nehéz" 19
"40" 40 "Nem volt" "Nehéz" 12
"41" 41 "Egyszerű" "Könnyű" 21
"42" 42 "Egyszerű" "Könnyű" 23
"43" 43 "Egyszerű" "Könnyű" 7
"44" 44 "Egyszerű" "Könnyű" 25
"45" 45 "Egyszerű" "Könnyű" 15
"46" 46 "Egyszerű" "Könnyű" 21
"47" 47 "Egyszerű" "Könnyű" 19
"48" 48 "Egyszerű" "Könnyű" 1
"49" 49 "Egyszerű" "Könnyű" 25
"50" 50 "Egyszerű" "Könnyű" 20
"51" 51 "Egyszerű" "Könnyű" 32
"52" 52 "Egyszerű" "Könnyű" 32
"53" 53 "Egyszerű" "Könnyű" 14
"54" 54 "Egyszerű" "Könnyű" 34
"55" 55 "Egyszerű" "Könnyű" 21
"56" 56 "Egyszerű" "Könnyű" 13
"57" 57 "Egyszerű" "Könnyű" 20
"58" 58 "Egyszerű" "Könnyű" 28
"59" 59 "Egyszerű" "Könnyű" 10
"60" 60 "Egyszerű" "Könnyű" 15
"61" 61 "Egyszerű" "Nehéz" 46
"62" 62 "Egyszerű" "Nehéz" 30
"63" 63 "Egyszerű" "Nehéz" 37
"64" 64 "Egyszerű" "Nehéz" 31
"65" 65 "Egyszerű" "Nehéz" 25
"66" 66 "Egyszerű" "Nehéz" 23
"67" 67 "Egyszerű" "Nehéz" 38
"68" 68 "Egyszerű" "Nehéz" 36
"69" 69 "Egyszerű" "Nehéz" 43
"70" 70 "Egyszerű" "Nehéz" 41
"71" 71 "Egyszerű" "Nehéz" 43
"72" 72 "Egyszerű" "Nehéz" 32
"73" 73 "Egyszerű" "Nehéz" 37
"74" 74 "Egyszerű" "Nehéz" 23
"75" 75 "Egyszerű" "Nehéz" 34
"76" 76 "Egyszerű" "Nehéz" 46
"77" 77 "Egyszerű" "Nehéz" 54
"78" 78 "Egyszerű" "Nehéz" 45
"79" 79 "Egyszerű" "Nehéz" 33
"80" 80 "Egyszerű" "Nehéz" 42
"81" 81 "Bonyolult" "Könnyű" 21
"82" 82 "Bonyolult" "Könnyű" 33
"83" 83 "Bonyolult" "Könnyű" 24
"84" 84 "Bonyolult" "Könnyű" 21
"85" 85 "Bonyolult" "Könnyű" 29
"86" 86 "Bonyolult" "Könnyű" 24
"87" 87 "Bonyolult" "Könnyű" 28
"88" 88 "Bonyolult" "Könnyű" 31
"89" 89 "Bonyolult" "Könnyű" 22
"90" 90 "Bonyolult" "Könnyű" 21
"91" 91 "Bonyolult" "Könnyű" 42
"92" 92 "Bonyolult" "Könnyű" 20
"93" 93 "Bonyolult" "Könnyű" 25
"94" 94 "Bonyolult" "Könnyű" 20
"95" 95 "Bonyolult" "Könnyű" 21
"96" 96 "Bonyolult" "Könnyű" 16
"97" 97 "Bonyolult" "Könnyű" 23
"98" 98 "Bonyolult" "Könnyű" 37
"99" 99 "Bonyolult" "Könnyű" 34
"100" 100 "Bonyolult" "Könnyű" 25
"101" 101 "Bonyolult" "Nehéz" 46
"102" 102 "Bonyolult" "Nehéz" 49
"103" 103 "Bonyolult" "Nehéz" 56
"104" 104 "Bonyolult" "Nehéz" 41
"105" 105 "Bonyolult" "Nehéz" 56
"106" 106 "Bonyolult" "Nehéz" 36
"107" 107 "Bonyolult" "Nehéz" 46
"108" 108 "Bonyolult" "Nehéz" 39
"109" 109 "Bonyolult" "Nehéz" 42
"110" 110 "Bonyolult" "Nehéz" 56
"111" 111 "Bonyolult" "Nehéz" 51
"112" 112 "Bonyolult" "Nehéz" 27
"113" 113 "Bonyolult" "Nehéz" 45
"114" 114 "Bonyolult" "Nehéz" 48
"115" 115 "Bonyolult" "Nehéz" 50
"116" 116 "Bonyolult" "Nehéz" 61
"117" 117 "Bonyolult" "Nehéz" 43
"118" 118 "Bonyolult" "Nehéz" 47
"119" 119 "Bonyolult" "Nehéz" 54
"120" 120 "Bonyolult" "Nehéz" 41
'), header=T, sep="")
d$vezetes <- factor(d$vezetes, levels=c("Könnyű", "Nehéz")) # szintsorrend beállítása
d$beszelgetes <- factor(d$beszelgetes, levels=c("Nem volt", "Egyszerű", "Bonyolult")) # szintsorrend beállítása
str(d) # az adattábla szerkezete## 'data.frame': 120 obs. of 4 variables:
## $ subject : int 1 2 3 4 5 6 7 8 9 10 ...
## $ beszelgetes: Factor w/ 3 levels "Nem volt","Egyszerű",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ vezetes : Factor w/ 2 levels "Könnyű","Nehéz": 1 1 1 1 1 1 1 1 1 1 ...
## $ hibak.szama: int 20 19 31 27 31 17 23 26 11 15 ...d # a beolvasott adattábla## subject beszelgetes vezetes hibak.szama
## 1 1 Nem volt Könnyű 20
## 2 2 Nem volt Könnyű 19
## 3 3 Nem volt Könnyű 31
## 4 4 Nem volt Könnyű 27
## 5 5 Nem volt Könnyű 31
## 6 6 Nem volt Könnyű 17
## 7 7 Nem volt Könnyű 23
## 8 8 Nem volt Könnyű 26
## 9 9 Nem volt Könnyű 11
## 10 10 Nem volt Könnyű 15
## 11 11 Nem volt Könnyű 13
## 12 12 Nem volt Könnyű 18
## 13 13 Nem volt Könnyű 21
## 14 14 Nem volt Könnyű 13
## 15 15 Nem volt Könnyű 13
## 16 16 Nem volt Könnyű 14
## 17 17 Nem volt Könnyű 20
## 18 18 Nem volt Könnyű 26
## 19 19 Nem volt Könnyű 20
## 20 20 Nem volt Könnyű 14
## 21 21 Nem volt Nehéz 10
## 22 22 Nem volt Nehéz 23
## 23 23 Nem volt Nehéz 31
## 24 24 Nem volt Nehéz 32
## 25 25 Nem volt Nehéz 24
## 26 26 Nem volt Nehéz 26
## 27 27 Nem volt Nehéz 46
## 28 28 Nem volt Nehéz 25
## 29 29 Nem volt Nehéz 23
## 30 30 Nem volt Nehéz 25
## 31 31 Nem volt Nehéz 13
## 32 32 Nem volt Nehéz 32
## 33 33 Nem volt Nehéz 32
## 34 34 Nem volt Nehéz 16
## 35 35 Nem volt Nehéz 26
## 36 36 Nem volt Nehéz 24
## 37 37 Nem volt Nehéz 11
## 38 38 Nem volt Nehéz 15
## 39 39 Nem volt Nehéz 19
## 40 40 Nem volt Nehéz 12
## 41 41 Egyszerű Könnyű 21
## 42 42 Egyszerű Könnyű 23
## 43 43 Egyszerű Könnyű 7
## 44 44 Egyszerű Könnyű 25
## 45 45 Egyszerű Könnyű 15
## 46 46 Egyszerű Könnyű 21
## 47 47 Egyszerű Könnyű 19
## 48 48 Egyszerű Könnyű 1
## 49 49 Egyszerű Könnyű 25
## 50 50 Egyszerű Könnyű 20
## 51 51 Egyszerű Könnyű 32
## 52 52 Egyszerű Könnyű 32
## 53 53 Egyszerű Könnyű 14
## 54 54 Egyszerű Könnyű 34
## 55 55 Egyszerű Könnyű 21
## 56 56 Egyszerű Könnyű 13
## 57 57 Egyszerű Könnyű 20
## 58 58 Egyszerű Könnyű 28
## 59 59 Egyszerű Könnyű 10
## 60 60 Egyszerű Könnyű 15
## 61 61 Egyszerű Nehéz 46
## 62 62 Egyszerű Nehéz 30
## 63 63 Egyszerű Nehéz 37
## 64 64 Egyszerű Nehéz 31
## 65 65 Egyszerű Nehéz 25
## 66 66 Egyszerű Nehéz 23
## 67 67 Egyszerű Nehéz 38
## 68 68 Egyszerű Nehéz 36
## 69 69 Egyszerű Nehéz 43
## 70 70 Egyszerű Nehéz 41
## 71 71 Egyszerű Nehéz 43
## 72 72 Egyszerű Nehéz 32
## 73 73 Egyszerű Nehéz 37
## 74 74 Egyszerű Nehéz 23
## 75 75 Egyszerű Nehéz 34
## 76 76 Egyszerű Nehéz 46
## 77 77 Egyszerű Nehéz 54
## 78 78 Egyszerű Nehéz 45
## 79 79 Egyszerű Nehéz 33
## 80 80 Egyszerű Nehéz 42
## 81 81 Bonyolult Könnyű 21
## 82 82 Bonyolult Könnyű 33
## 83 83 Bonyolult Könnyű 24
## 84 84 Bonyolult Könnyű 21
## 85 85 Bonyolult Könnyű 29
## 86 86 Bonyolult Könnyű 24
## 87 87 Bonyolult Könnyű 28
## 88 88 Bonyolult Könnyű 31
## 89 89 Bonyolult Könnyű 22
## 90 90 Bonyolult Könnyű 21
## 91 91 Bonyolult Könnyű 42
## 92 92 Bonyolult Könnyű 20
## 93 93 Bonyolult Könnyű 25
## 94 94 Bonyolult Könnyű 20
## 95 95 Bonyolult Könnyű 21
## 96 96 Bonyolult Könnyű 16
## 97 97 Bonyolult Könnyű 23
## 98 98 Bonyolult Könnyű 37
## 99 99 Bonyolult Könnyű 34
## 100 100 Bonyolult Könnyű 25
## 101 101 Bonyolult Nehéz 46
## 102 102 Bonyolult Nehéz 49
## 103 103 Bonyolult Nehéz 56
## 104 104 Bonyolult Nehéz 41
## 105 105 Bonyolult Nehéz 56
## 106 106 Bonyolult Nehéz 36
## 107 107 Bonyolult Nehéz 46
## 108 108 Bonyolult Nehéz 39
## 109 109 Bonyolult Nehéz 42
## 110 110 Bonyolult Nehéz 56
## 111 111 Bonyolult Nehéz 51
## 112 112 Bonyolult Nehéz 27
## 113 113 Bonyolult Nehéz 45
## 114 114 Bonyolult Nehéz 48
## 115 115 Bonyolult Nehéz 50
## 116 116 Bonyolult Nehéz 61
## 117 117 Bonyolult Nehéz 43
## 118 118 Bonyolult Nehéz 47
## 119 119 Bonyolult Nehéz 54
## 120 120 Bonyolult Nehéz 41Leíróstatisztikai mutatók. A két faktor változó (a vezetes 2 szinttel és a beszelgetes 3 szinttel) összesen 6 csoportot határoz meg. Az egyes csoportokban a leíró statisztikai változókat a szokásos függvényekkel határozzuk meg (psych csomag describeBy(), DescTools csomag Desc()), valamint a tapply() függvénnyel az átlagok, szórások és a csoportok mintaelemszámát is kiíratjuk.
library(psych)
psych::describeBy(d$hibak.szama, d[,c("vezetes", "beszelgetes")], mat = T)## item group1 group2 vars n mean sd median trimmed mad min
## 11 1 Könnyű Nem volt 1 20 19.60 6.107803 19.5 19.1250 8.1543 11
## 12 2 Nehéz Nem volt 1 20 23.25 8.961174 24.0 22.8750 11.1195 10
## 13 3 Könnyű Egyszerű 1 20 19.80 8.507582 20.5 20.1250 8.1543 1
## 14 4 Nehéz Egyszerű 1 20 36.95 8.274724 37.0 37.0625 8.8956 23
## 15 5 Könnyű Bonyolult 1 20 25.85 6.627495 24.0 25.1250 5.1891 16
## 16 6 Nehéz Bonyolult 1 20 46.70 8.013804 46.5 47.1250 7.4130 27
## max range skew kurtosis se
## 11 31 20 0.43138298 -1.0634815 1.365746
## 12 46 36 0.45986114 -0.0743921 2.003779
## 13 34 33 -0.24755355 -0.5530346 1.902353
## 14 54 31 -0.02575589 -0.7991620 1.850284
## 15 42 26 0.82043108 -0.2629233 1.481953
## 16 61 34 -0.38873426 -0.1192823 1.791941library(DescTools)
Desc(hibak.szama ~ vezetes * beszelgetes, data = d)## -------------------------------------------------------------------------
## hibak.szama ~ vezetes
##
## Summary:
## n pairs: 120, valid: 120 (100.0%), missings: 0 (0.0%), groups: 2
##
##
## Könnyű Nehéz
## mean 21.7500000 35.6333333
## median 21.0000000 36.5000000
## sd 7.6171639 12.7544830
## IQR 9.2500000 21.0000000
## n 60 60
## np 50.0000000% 50.0000000%
## NAs 0 0
## 0s 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 35.603, df = 1, p-value = 0.00000000242
## -------------------------------------------------------------------------
## hibak.szama ~ beszelgetes
##
## Summary:
## n pairs: 120, valid: 120 (100.0%), missings: 0 (0.0%), groups: 3
##
##
## Nem volt Egyszerű Bonyolult
## mean 21.4250000 28.3750000 36.2750000
## median 20.5000000 29.0000000 36.5000000
## sd 7.7918021 12.0014689 12.8122287
## IQR 11.2500000 16.2500000 22.2500000
## n 40 40 40
## np 33.3333333% 33.3333333% 33.3333333%
## NAs 0 0 0
## 0s 0 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 26.629, df = 2, p-value = 0.00000165
## -------------------------------------------------------------------------
## hibak.szama ~ vezetes:beszelgetes
##
## Summary:
## n pairs: 120, valid: 120 (100.0%), missings: 0 (0.0%), groups: 6
##
##
## Könnyű:Nem volt Nehéz:Nem volt Könnyű:Egyszerű
## mean 19.6000000 23.2500000 19.8000000
## median 19.5000000 24.0000000 20.5000000
## sd 6.1078035 8.9611736 8.5075818
## IQR 9.7500000 11.5000000 10.2500000
## n 20 20 20
## np 16.6666667% 16.6666667% 16.6666667%
## NAs 0 0 0
## 0s 0 0 0
##
## Nehéz:Egyszerű Könnyű:Bonyolult Nehéz:Bonyolult
## mean 36.9500000 25.8500000 46.7000000
## median 37.0000000 24.0000000 46.5000000
## sd 8.2747237 6.6274946 8.0138039
## IQR 11.2500000 8.5000000 10.0000000
## n 20 20 20
## np 16.6666667% 16.6666667% 16.6666667%
## NAs 0 0 0
## 0s 0 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 69.378, df = 5, p-value = 1.38e-13tapply(d$hibak.szama, d[,c("vezetes", "beszelgetes")], mean, na.rm = T) # átlagok## beszelgetes
## vezetes Nem volt Egyszerű Bonyolult
## Könnyű 19.60 19.80 25.85
## Nehéz 23.25 36.95 46.70tapply(d$hibak.szama, d[,c("vezetes", "beszelgetes")], sd, na.rm = T) # szórások## beszelgetes
## vezetes Nem volt Egyszerű Bonyolult
## Könnyű 6.107803 8.507582 6.627495
## Nehéz 8.961174 8.274724 8.013804tapply(d$hibak.szama, d[,c("vezetes", "beszelgetes")], function(x) sum(!is.na(x))) # csoportok elemszáma## beszelgetes
## vezetes Nem volt Egyszerű Bonyolult
## Könnyű 20 20 20
## Nehéz 20 20 20Grafikus vizsgálatok. A fenti átlagok jobban áttekinthetők átlagábrák segítségével.
library(PASWR2)
twoway.plots(Y = d$hibak.szama, fac1 = d$beszelgetes, fac2 = d$vezetes)
library(yarrr)
pirateplot(formula = hibak.szama ~ vezetes * beszelgetes, data = d, hdi.o = 0, line.o = 0,
theme.o = 1, pal = "google")
library(ggplot2)
pd <- position_dodge(0.1)
pic.d.gog.1 <- ggplot(data=d, aes(x=beszelgetes, y=hibak.szama, colour=vezetes)) +
stat_summary(fun.data=mean_cl_normal, geom="line", size=1, aes(group=vezetes), position=pd) +
stat_summary(fun.data=mean_cl_normal, geom="errorbar", size=1, width=0.1, position=pd) +
stat_summary(fun.y=mean, geom="point", size=4, shape=21, fill="white", position=pd) +
coord_cartesian(ylim = c(0, 50)) + theme_bw() + labs(x="Beszélgetés", y="Idő") +
scale_color_discrete(guide = guide_legend(title = "Vezetési feladat"))
pic.d.gog.1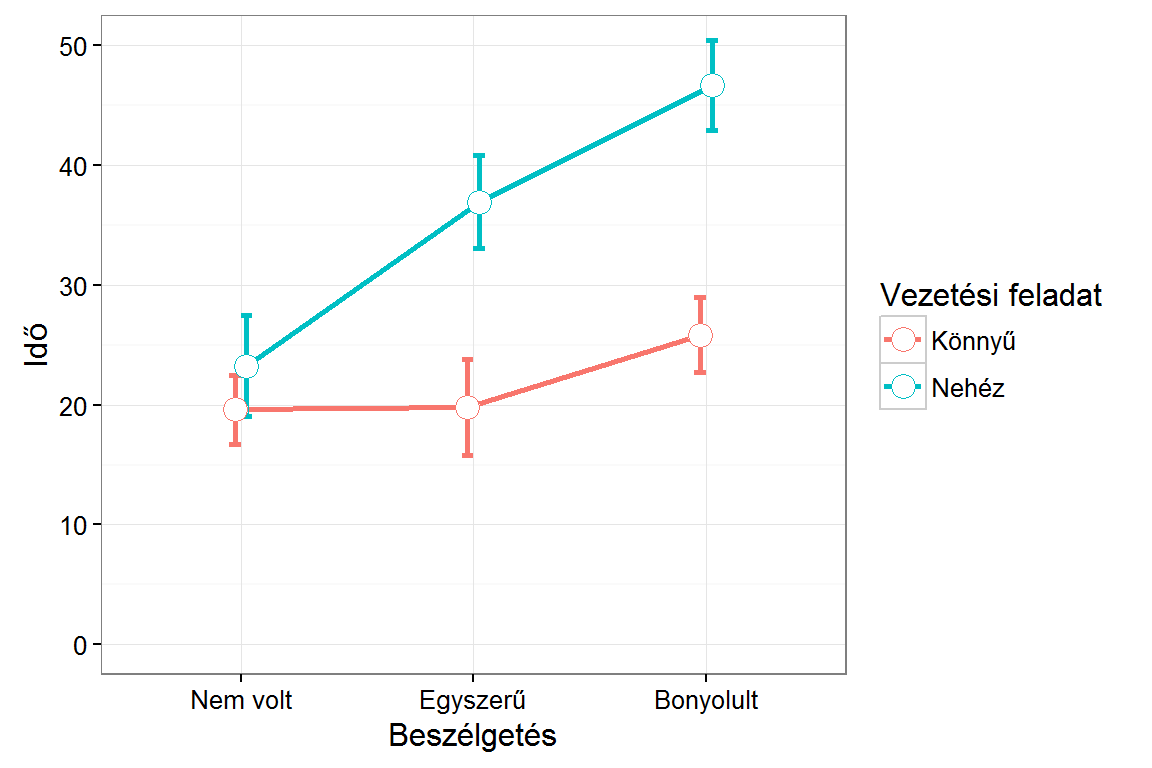
A fenti átlagábrákról az egyes csoportok átlagai leolvashatók, de az interakció ténye is világossá válik.
Alkalmazási feltételek. A kétszempontos varianciaelemzés egyik alkalmazási feltétele a szóráshomogenitás, amely a Levene-próbával vizsgálható. A DescTools csomag LeveneTest() függvényének megadhatjuk a modellformulát.
library(DescTools)
LeveneTest(hibak.szama ~ vezetes * beszelgetes, data = d, center = mean)## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 5 0.4816 0.7894
## 114A Levene-próba igazolta, hogy a szóráshomogenitási feltétel fenáll (\(F(5,114)=0,4816; p=0,7894\)).
A kétszempontos varianciaelemzés másik feltétele, hogy két faktor által meghatározott összes csoportban a függő változó közelítőleg normalis eloszlást kövessen. A Shapiro–Wilk-próbákat a shapiro.test() függvénnyel hajtjuk végre.
by(d$hibak.szama, d[,c("vezetes", "beszelgetes")], shapiro.test)## vezetes: Könnyű
## beszelgetes: Nem volt
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93135, p-value = 0.1639
##
## --------------------------------------------------------
## vezetes: Nehéz
## beszelgetes: Nem volt
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93849, p-value = 0.2245
##
## --------------------------------------------------------
## vezetes: Könnyű
## beszelgetes: Egyszerű
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.9749, p-value = 0.8531
##
## --------------------------------------------------------
## vezetes: Nehéz
## beszelgetes: Egyszerű
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97188, p-value = 0.794
##
## --------------------------------------------------------
## vezetes: Könnyű
## beszelgetes: Bonyolult
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.9141, p-value = 0.07634
##
## --------------------------------------------------------
## vezetes: Nehéz
## beszelgetes: Bonyolult
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97483, p-value = 0.8516A fenti Shapiro–Wilk-próbák igazolják a normalitási feltétel teljesülését (mindegyik csoportban \(p>0,07\)).
A normalitást a reziduumok esetében is ellenőrizzük! A residuals() függvénnyel az illesztett modellből kinyerhetők a reziduumok, melyekre grafikus módszerrel és Shapiro–Wilk-próbával is ellenőrizhetjük a normalitási feltételt.
aov.d <- aov(hibak.szama ~ vezetes * beszelgetes, data = d) # a modell illesztése
aov.d.residuals <- residuals(object = aov.d) # reziduumok kiszámítása
par(mfrow=c(1,2))
hist(aov.d.residuals) # hisztogram a reziduumokra
qqnorm(aov.d.residuals); qqline(aov.d.residuals) # QQ-ábra a reziduumokra
par(mfrow=c(1,1))
shapiro.test(aov.d.residuals) # Shapiro-Wilk-próba a reziduumokra##
## Shapiro-Wilk normality test
##
## data: aov.d.residuals
## W = 0.99377, p-value = 0.8738A fenti ábrák és a Shapiro–Wilk-próba (\(W=0,9938; p=0,8783\)) is alátámasztja, hogy az reziduumok normalitása nem sérül.
Kétszempontos varianciaelemzés végrehajtása. A kétszempontos varianciaelemzés az aov() függvénnyel is végrehajtható, ahol a modell argumentum: formula=hibak.szama~vezetes*beszelgetes. Az ANOVA táblázatot a summary() függvénnyel kérhetjük le.
aov.d <- aov(formula = hibak.szama ~ vezetes * beszelgetes, data = d)
summary(aov.d)## Df Sum Sq Mean Sq F value Pr(>F)
## vezetes 1 5782 5782 94.64 < 2e-16
## beszelgetes 2 4416 2208 36.14 6.98e-13
## vezetes:beszelgetes 2 1639 820 13.41 5.86e-06
## Residuals 114 6965 61A kétszempontos varianciaelemzés eredménye azt mondhatjuk, hogy a vezetési feladat nehézsége szignifikánsan hat a hibázások számára (\(F(1, 114)=94,64; p<0,0001\)), valamint a beszélgetés faktor is szignifikáns főhatású (\(F(2, 114)=36,14; p<0,0001\)). Az két faktor interakciója is szignifikáns (\(F(2, 114)=13,41; p<0,0001\)), vagyis a vezetési feladat nehézségének hatását a hibázások számára módosítja a beszélgetés faktor. A korábban megrajzolt átlagábrákról leolvasható az interakció hatása: a beszélgetés bonyolultságának növekedése mentén megemelkedik a könnyű és nehéz vezetési feladat közötti hibázások számának különbsége, vagyis a bonyolultabb telefonbeszélgetés erősíti a hibázások számának növekedését.
Kétszempontos varianciaelemzés utóelemzése.
Mutassuk ki számszerűen is ezt az erősítő hatást egyszerű hatások (simple effect) vizsgálatával. Szűréssel hozzuk létre a telefonbeszélgetés faktor alapján a minta három csoportját (d.1, d.2 és d.3). Ezekre az almintákra vizsgáljuk meg a vezetési feladat nehézségének hatását. Mivel a vezetes két szinttel rendelkezik, a userfriendlyscience csomag oneway() függvénye mellett az lsr csomag independentSamplesTTest() függvényével is bemutatjuk az egyszerű hatások vizsgálatát.
library(userfriendlyscience)
d.1 <- d[d$beszelgetes=="Nem volt",]
d.2 <- d[d$beszelgetes=="Egyszerű",]
d.3 <- d[d$beszelgetes=="Bonyolult",]
oneway(y = d.1$hibak.szama, x = d.1$vezetes, digits = 4, pvalueDigits = 4)## ### Oneway Anova for y=hibak.szama and x=vezetes (groups: Könnyű, Nehéz)
##
## Eta Squared: 95% CI = [0; 0.2002], point estimate = 0.0563
##
## SS Df MS F p
## Between groups (error + effect) 133.225 1 133.225 2.2656 .1405
## Within groups (error only) 2234.55 38 58.8039oneway(y = d.2$hibak.szama, x = d.2$vezetes, digits = 4, pvalueDigits = 4)## ### Oneway Anova for y=hibak.szama and x=vezetes (groups: Könnyű, Nehéz)
##
## Eta Squared: 95% CI = [0.3245; 0.6422], point estimate = 0.5236
##
## SS Df MS F p
## Between groups (error + effect) 2941.225 1 2941.225 41.7639 < .0001
## Within groups (error only) 2676.15 38 70.425oneway(y = d.3$hibak.szama, x = d.3$vezetes, digits = 4, pvalueDigits = 4)## ### Oneway Anova for y=hibak.szama and x=vezetes (groups: Könnyű, Nehéz)
##
## Eta Squared: 95% CI = [0.519; 0.7608], point estimate = 0.679
##
## SS Df MS F p
## Between groups (error + effect) 4347.225 1 4347.225 80.3964 < .0001
## Within groups (error only) 2054.75 38 54.0724library(lsr)
independentSamplesTTest(formula = hibak.szama ~ vezetes, data = d.1, var.equal = T)##
## Student's independent samples t-test
##
## Outcome variable: hibak.szama
## Grouping variable: vezetes
##
## Descriptive statistics:
## Könnyű Nehéz
## mean 19.600 23.250
## std dev. 6.108 8.961
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: -1.505
## degrees of freedom: 38
## p-value: 0.141
##
## Other information:
## two-sided 95% confidence interval: [-8.559, 1.259]
## estimated effect size (Cohen's d): 0.476independentSamplesTTest(formula = hibak.szama ~ vezetes, data = d.2, var.equal = T)##
## Student's independent samples t-test
##
## Outcome variable: hibak.szama
## Grouping variable: vezetes
##
## Descriptive statistics:
## Könnyű Nehéz
## mean 19.800 36.950
## std dev. 8.508 8.275
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: -6.463
## degrees of freedom: 38
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [-22.522, -11.778]
## estimated effect size (Cohen's d): 2.044independentSamplesTTest(formula = hibak.szama ~ vezetes, data = d.3, var.equal = T)##
## Student's independent samples t-test
##
## Outcome variable: hibak.szama
## Grouping variable: vezetes
##
## Descriptive statistics:
## Könnyű Nehéz
## mean 25.850 46.700
## std dev. 6.627 8.014
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: -8.966
## degrees of freedom: 38
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [-25.557, -16.143]
## estimated effect size (Cohen's d): 2.835A telefont nem használók körében nem volt szignifikáns különbség a hibázások számában (egyszempontos varianciaelemzés: \(\eta^2=0,06; F(1,38)=2,2656; p=0,1405\); kétmintás t-próba: Cohen-d\(=0,48; t=-1,505; p=0,141\)). Az egyszerű telefonbeszélgetést folytatók körében már szignifikáns a különbség a két vezetési feladat esetében (egyszempontos varianciaelemzés: \(\eta^2=0,52; F(1,38)=41,7639; p<0,0001\); kétmintás t-próba: Cohen-d\(=2,04; t=-6,463; p<0,001\)). A bonyolult telefonbeszélgetést folytatók körében is szignifikáns a különbség a hibázások számában, de a vezetési feladat nehézségének hatása tovább nő (egyszempontos varianciaelemzés: \(\eta^2=0,68; F(1,38)=80,3964; p<0,0001\); kétmintás t-próba: Cohen-d\(=2,84; t=-8,966; p<0,001\)).
Alternatívák kétszempontos varianciaelemzésre. Használjuk a lessR csomag ANOVA() függvényét!
library(lessR)
ANOVA(my.formula = hibak.szama ~ vezetes * beszelgetes, data = d) # kétszempontos varianciaelemzés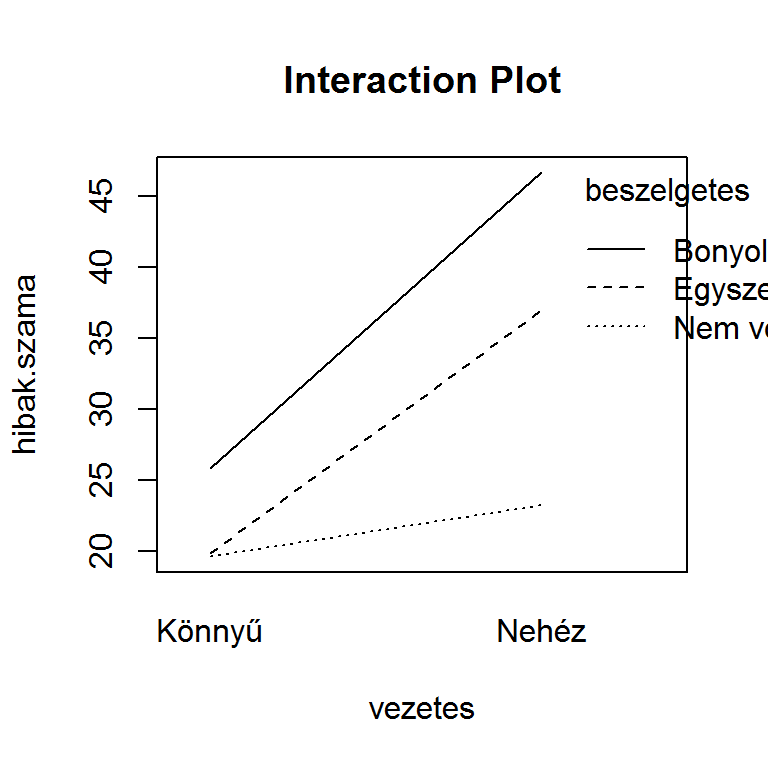
## BACKGROUND
##
## Response Variable: hibak.szama
##
## Factor Variable 1: vezetes
## Levels: Könnyű Nehéz
##
## Factor Variable 2: beszelgetes
## Levels: Nem volt Egyszerű Bonyolult
##
## Number of cases (rows) of data: 120
## Number of cases retained for analysis: 120
##
## The design is balanced
##
## Two-way Between Groups ANOVA
##
##
## DESCRIPTIVE STATISTICS
##
## Cell Sample Size: 20
##
##
## vezetes
## beszelgetes Könnyű Nehéz
## Nem volt 19.60 23.25
## Egyszerű 19.80 36.95
## Bonyolult 25.85 46.70
##
##
## vezetes
## ----------------
## Könnyű Nehéz
## 1 21.75 35.63
##
## beszelgetes
## -------------------------------
## Nem.volt Egyszerű Bonyolult
## 1 21.43 28.38 36.27
##
##
## 28.692
##
##
## vezetes
## beszelgetes Könnyű Nehéz
## Nem volt 6.11 8.96
## Egyszerű 8.51 8.27
## Bonyolult 6.63 8.01
##
##
## BASIC ANALYSIS
##
## df Sum Sq Mean Sq F-value p-value
## vezetes 1 5782.41 5782.41 94.64 0.0000
## beszelgetes 2 4416.47 2208.23 36.14 0.0000
## vezetes:beszelgetes 2 1639.27 819.63 13.41 0.0000
## Residuals 114 6965.45 61.10
##
##
## Partial Omega Squared for vezetes: 0.44
## Partial Omega Squared for beszelgetes: 0.37
## Partial Omega Squared for vezetes & beszelgetes: 0.17
##
## Cohen's f for vezetes: 0.88
## Cohen's f for beszelgetes: 0.77
## Cohen's f for vezetes_&_beszelgetes: 0.45
##
##
##
## Family-wise Confidence Level: 0.95
##
## Factor: vezetes
## --------------------------------------
## diff lwr upr p adj
## Nehéz-Könnyű 13.88 11.06 16.71 0.00
##
## Factor: beszelgetes
## --------------------------------------------
## diff lwr upr p adj
## Egyszerű-Nem volt 6.95 2.80 11.10 0.00
## Bonyolult-Nem volt 14.85 10.70 19.00 0.00
## Bonyolult-Egyszerű 7.90 3.75 12.05 0.00
##
## Cell Means
## ------------------------------------------------------------
## diff lwr upr p adj
## Nehéz:Nem volt-Könnyű:Nem volt 3.65 -3.52 10.82 0.68
## Könnyű:Egyszerű-Könnyű:Nem volt 0.20 -6.97 7.37 1.00
## Nehéz:Egyszerű-Könnyű:Nem volt 17.35 10.18 24.52 0.00
## Könnyű:Bonyolult-Könnyű:Nem volt 6.25 -0.92 13.42 0.12
## Nehéz:Bonyolult-Könnyű:Nem volt 27.10 19.93 34.27 0.00
## Könnyű:Egyszerű-Nehéz:Nem volt -3.45 -10.62 3.72 0.73
## Nehéz:Egyszerű-Nehéz:Nem volt 13.70 6.53 20.87 0.00
## Könnyű:Bonyolult-Nehéz:Nem volt 2.60 -4.57 9.77 0.90
## Nehéz:Bonyolult-Nehéz:Nem volt 23.45 16.28 30.62 0.00
## Nehéz:Egyszerű-Könnyű:Egyszerű 17.15 9.98 24.32 0.00
## Könnyű:Bonyolult-Könnyű:Egyszerű 6.05 -1.12 13.22 0.15
## Nehéz:Bonyolult-Könnyű:Egyszerű 26.90 19.73 34.07 0.00
## Könnyű:Bonyolult-Nehéz:Egyszerű -11.10 -18.27 -3.93 0.00
## Nehéz:Bonyolult-Nehéz:Egyszerű 9.75 2.58 16.92 0.00
## Nehéz:Bonyolult-Könnyű:Bonyolult 20.85 13.68 28.02 0.00
##
##
## RESIDUALS
##
## Fitted Values, Residuals, Standardized Residuals
## [sorted by Standardized Residuals, ignoring + or - sign]
## [res.rows = 20, out of 120 cases (rows) of data, or res.rows="all"]
## -------------------------------------------------------------
## vezetes beszelgetes hibak.szama fitted residual z-resid
## 27 Nehéz Nem volt 46 23.25 22.75 2.99
## 112 Nehéz Bonyolult 27 46.70 -19.70 -2.59
## 48 Könnyű Egyszerű 1 19.80 -18.80 -2.47
## 77 Nehéz Egyszerű 54 36.95 17.05 2.24
## 91 Könnyű Bonyolult 42 25.85 16.15 2.12
## 116 Nehéz Bonyolult 61 46.70 14.30 1.88
## 54 Könnyű Egyszerű 34 19.80 14.20 1.86
## 66 Nehéz Egyszerű 23 36.95 -13.95 -1.83
## 74 Nehéz Egyszerű 23 36.95 -13.95 -1.83
## 21 Nehéz Nem volt 10 23.25 -13.25 -1.74
## 43 Könnyű Egyszerű 7 19.80 -12.80 -1.68
## 37 Nehéz Nem volt 11 23.25 -12.25 -1.61
## 51 Könnyű Egyszerű 32 19.80 12.20 1.60
## 52 Könnyű Egyszerű 32 19.80 12.20 1.60
## 65 Nehéz Egyszerű 25 36.95 -11.95 -1.57
## 5 Könnyű Nem volt 31 19.60 11.40 1.50
## 3 Könnyű Nem volt 31 19.60 11.40 1.50
## 40 Nehéz Nem volt 12 23.25 -11.25 -1.48
## 98 Könnyű Bonyolult 37 25.85 11.15 1.46
## 106 Nehéz Bonyolult 36 46.70 -10.70 -1.408.3.3 Példa. Állatok memóriája.
Egy kísérletben állatok memória-folyamatait vizsgáljuk. A tanulási szakaszban az állatnak úgy kell átlépnie egy felfestett vonalon, hogy közben félelemkeltő ingert mutatunk be számára. Miután ezt többször megismételjük, következik a tesztfázis, ahol újra a vonal átlépése a feladata (félelemkeltő inger nélkül). Ekkor megmérjük, hogy a vonal átlépéséhez mennyi időre van szüksége, ez lesz a függő változó. Az állatokat három csoportba soroltuk abból a szempontból, hogy az agykéreg melyik részébe ültettünk be előzőleg elektródákat (Semleges terület, A terület, B terület). Mindegyik csoport tovább bomlik az elektromos stimuláció késleltetése (50, 100 és 150 ms) szerint, ugyanis a tanulás során a vonal átlépése és a félelemkeltő inger bemutatása után az elektródákon keresztül a késleltetési idő lejárta után stimuláltuk az adott agyterületet. Ha a stimulált agyterület része a memóriának, akkor a stimuláció feltételezhetően zavarja a tanulás folyamatát, így az állat minden nehézség nélkül fogja átlépni a vonalat. Varianciaelemzéssel vizsgáljuk meg, hogy a függő változó értékeit mely tényezők befolyásolják. Az adatok a következő táblázatok tartalmazzák.
Forrás: (Howell 2013, 456)
Semleges terület:
| 50 ms | 100 ms | 150 ms |
|---|---|---|
| 25 | 30 | 28 |
| 30 | 25 | 31 |
| 28 | 27 | 26 |
| 40 | 35 | 20 |
| 20 | 23 | 35 |
A terület:
| 50 ms | 100 ms | 150 ms |
|---|---|---|
| 11 | 31 | 23 |
| 18 | 20 | 28 |
| 26 | 22 | 35 |
| 15 | 23 | 27 |
| 14 | 19 | 21 |
B terület:
| 50 ms | 100 ms | 150 ms |
|---|---|---|
| 23 | 18 | 28 |
| 30 | 24 | 21 |
| 18 | 9 | 30 |
| 28 | 16 | 30 |
| 23 | 13 | 23 |
Adatok beolvasása. Hozzuk létre be a fenti táblázatok alapján az egyes területekre vonatkozó mért adatokat (d.semleges, d.A.terulet és d.B.terulet), végezzük el a hosszú adatformára alakításukat, majd fűzzük őket össze egy d adattáblába.
d.semleges <- read.table(file = textConnection("
ms.50 ms.100 ms.150
25 30 28
30 25 31
28 27 26
40 35 20
20 23 35
"), header=T, sep="")
library(reshape2)
d.semleges <- melt(d.semleges, id.vars = NULL, value.name = "ido", variable.name = "varakozasi.ido") # szélesből- hosszú átalakítás
d.semleges$terulet <- "Semleges" # a terület címke erre a csoportra
d.A.terulet <- read.table(file = textConnection("
ms.50 ms.100 ms.150
11 31 23
18 20 28
26 22 35
15 23 27
14 19 21
"), header=T, sep="")
library(reshape2)
d.A.terulet <- melt(d.A.terulet, id.vars = NULL, value.name = "ido", variable.name = "varakozasi.ido") # szélesből- hosszú átalakítás
d.A.terulet$terulet <- "A.terulet" # a terület címke erre a csoportra
d.B.terulet <- read.table(file = textConnection("
ms.50 ms.100 ms.150
23 18 28
30 24 21
18 9 30
28 16 30
23 13 23
"), header=T, sep="")
library(reshape2)
d.B.terulet <- melt(d.B.terulet, id.vars = NULL, value.name = "ido", variable.name = "varakozasi.ido") # szélesből- hosszú átalakítás
d.B.terulet$terulet <- "B.terulet" # a terület címke erre a csoportra
d <- rbind(d.semleges, d.A.terulet, d.B.terulet) # adattábla létrehozása
d$terulet <- factor(d$terulet) # faktorrá konvertálás
d$terulet <- factor(d$terulet, levels = c("Semleges", "A.terulet", "B.terulet")) # faktorszintek sorrendjének beállítása
d$varakozasi.ido <- factor(d$varakozasi.ido, levels = c("ms.50", "ms.100", "ms.150")) # faktorszintek sorrendjének beállítása
str(d) # adattábla szerkezete## 'data.frame': 45 obs. of 3 variables:
## $ varakozasi.ido: Factor w/ 3 levels "ms.50","ms.100",..: 1 1 1 1 1 2 2 2 2 2 ...
## $ ido : int 25 30 28 40 20 30 25 27 35 23 ...
## $ terulet : Factor w/ 3 levels "Semleges","A.terulet",..: 1 1 1 1 1 1 1 1 1 1 ...d # adattábla tartalma ## varakozasi.ido ido terulet
## 1 ms.50 25 Semleges
## 2 ms.50 30 Semleges
## 3 ms.50 28 Semleges
## 4 ms.50 40 Semleges
## 5 ms.50 20 Semleges
## 6 ms.100 30 Semleges
## 7 ms.100 25 Semleges
## 8 ms.100 27 Semleges
## 9 ms.100 35 Semleges
## 10 ms.100 23 Semleges
## 11 ms.150 28 Semleges
## 12 ms.150 31 Semleges
## 13 ms.150 26 Semleges
## 14 ms.150 20 Semleges
## 15 ms.150 35 Semleges
## 16 ms.50 11 A.terulet
## 17 ms.50 18 A.terulet
## 18 ms.50 26 A.terulet
## 19 ms.50 15 A.terulet
## 20 ms.50 14 A.terulet
## 21 ms.100 31 A.terulet
## 22 ms.100 20 A.terulet
## 23 ms.100 22 A.terulet
## 24 ms.100 23 A.terulet
## 25 ms.100 19 A.terulet
## 26 ms.150 23 A.terulet
## 27 ms.150 28 A.terulet
## 28 ms.150 35 A.terulet
## 29 ms.150 27 A.terulet
## 30 ms.150 21 A.terulet
## 31 ms.50 23 B.terulet
## 32 ms.50 30 B.terulet
## 33 ms.50 18 B.terulet
## 34 ms.50 28 B.terulet
## 35 ms.50 23 B.terulet
## 36 ms.100 18 B.terulet
## 37 ms.100 24 B.terulet
## 38 ms.100 9 B.terulet
## 39 ms.100 16 B.terulet
## 40 ms.100 13 B.terulet
## 41 ms.150 28 B.terulet
## 42 ms.150 21 B.terulet
## 43 ms.150 30 B.terulet
## 44 ms.150 30 B.terulet
## 45 ms.150 23 B.teruletLeíróstatisztikai mutatók. A terulet és a varakozasi.ido faktor 3-3 szinttel rendelkezik, így összesen 9 csoportunk van. Határozzuk meg a tapply() függvénnyel ezekben a csoportokban az átlagokat, szórásokat és a csoportok mintaelemszámát!
tapply(d$ido, d[,c("terulet", "varakozasi.ido")], mean, na.rm = T) # átlagok## varakozasi.ido
## terulet ms.50 ms.100 ms.150
## Semleges 28.6 28 28.0
## A.terulet 16.8 23 26.8
## B.terulet 24.4 16 26.4tapply(d$ido, d[,c("terulet", "varakozasi.ido")], sd, na.rm = T) # szórások## varakozasi.ido
## terulet ms.50 ms.100 ms.150
## Semleges 7.402702 4.690416 5.612486
## A.terulet 5.718391 4.743416 5.403702
## B.terulet 4.722288 5.612486 4.159327tapply(d$ido, d[,c("terulet", "varakozasi.ido")], function(x) sum(!is.na(x))) # csoportok elemszáma## varakozasi.ido
## terulet ms.50 ms.100 ms.150
## Semleges 5 5 5
## A.terulet 5 5 5
## B.terulet 5 5 5Grafikus vizsgálatok.
library(PASWR2)
twoway.plots(Y = d$ido, fac1 = d$terulet, fac2 = d$varakozasi.ido)
library(yarrr)
pirateplot(formula = ido ~ varakozasi.ido + terulet, data = d, hdi.o = 0, line.o = 0,
theme.o = 1, pal = "google")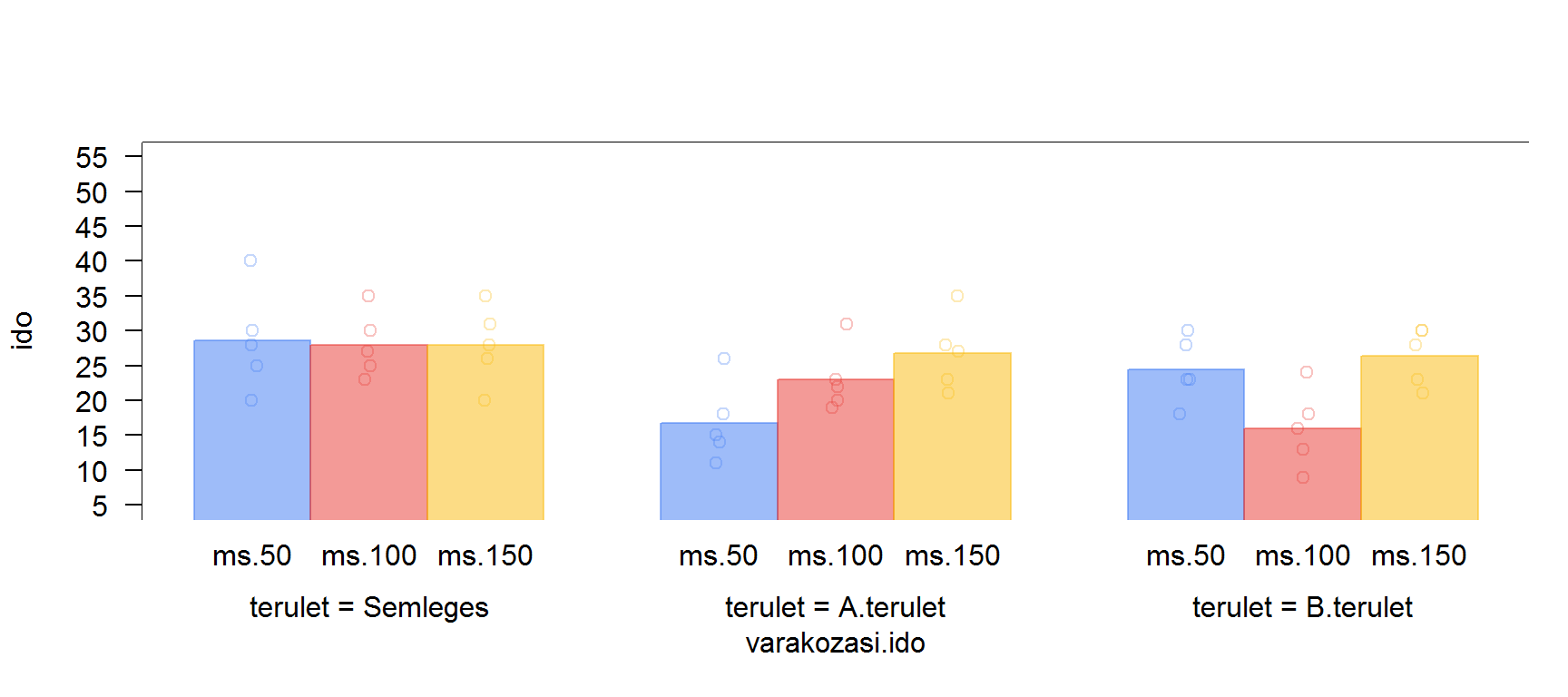
library(ggplot2)
pd <- position_dodge(0.1)
pic.d.gog.1 <- ggplot(data=d, aes(x=terulet, y=ido, colour=varakozasi.ido)) +
stat_summary(fun.data=mean_cl_normal, geom="line", size=1, aes(group=varakozasi.ido), position=pd) +
stat_summary(fun.data=mean_cl_normal, geom="errorbar", size=1, width=0.1, position=pd) +
stat_summary(fun.y=mean, geom="point", size=4, shape=21, fill="white", position=pd) +
coord_cartesian(ylim = c(0, 40)) + theme_bw() + labs(x="Terület", y="Idő") +
scale_color_discrete(guide = guide_legend(title = "Várakozási idő"))
pic.d.gog.1
Kétszempontos varianciaelemzés végrehajtása.
aov.d <- aov(ido ~ terulet * varakozasi.ido, data = d)
summary(aov.d)## Df Sum Sq Mean Sq F value Pr(>F)
## terulet 2 356.0 178.02 6.074 0.00534
## varakozasi.ido 2 188.6 94.29 3.217 0.05184
## terulet:varakozasi.ido 4 372.0 92.99 3.172 0.02482
## Residuals 36 1055.2 29.31A kétszempontos varianciaelemzés szignifikáns főhatást mutatott ki a terület faktor esetében (\(F(2,36)=6,074; p=0,0053\)), míg a várakozási idő faktornak nincs hatása (\(F(2,36)=3,217; p=0,0518\)). A két faktor interakciója is szignifikáns (\(F(4,36)=3,172; p=0,0248\)).
Utóelemzés. A terület faktor szignifikáns főhatását vizsgáljuk meg közelebbről. Végezzünk Tukey-próbát a terület faktorra a TukeyHSD() függvénnyel, amelyben használjuk a which="terulet" argumentumot.
TukeyHSD(aov.d, which = "terulet")## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = ido ~ terulet * varakozasi.ido, data = d)
##
## $terulet
## diff lwr upr p adj
## A.terulet-Semleges -6.00000000 -10.832140 -1.167860 0.0120787
## B.terulet-Semleges -5.93333333 -10.765473 -1.101193 0.0131618
## B.terulet-A.terulet 0.06666667 -4.765473 4.898807 0.9993732A Tukey-próba alapján azt mondhatjuk, hogy a Semleges területre beültetett elektródák esetében mért idő szignifikánsan különbözik az A területre és a B területre beültetett elektródák esetén mért időktől (mindkét esetben \(p<0,0132\)).
A szignifikáns interakció jellegét a 3 egyszempontos varianciaelemzéssel vizsgáljuk meg, a késleltetési idő három szintén.
d.ms.50 <- d[d$varakozasi.ido=="ms.50",] # szűrés, 50 ms
d.ms.100 <- d[d$varakozasi.ido=="ms.100",] # szűrés, 100 ms
d.ms.150 <- d[d$varakozasi.ido=="ms.150",] # szűrés, 150 ms
aov.ms.50 <- aov(formula = ido ~ terulet, data = d.ms.50) # egyszempontos varianciaelemzés, 50 ms
aov.ms.100 <- aov(formula = ido ~ terulet, data = d.ms.100) # egyszempontos varianciaelemzés, 100 ms
aov.ms.150 <- aov(formula = ido ~ terulet, data = d.ms.150) # egyszempontos varianciaelemzés, 150 ms
summary(aov.ms.50) # ANOVA tábla, 50 ms ## Df Sum Sq Mean Sq F value Pr(>F)
## terulet 2 357.7 178.9 4.887 0.028
## Residuals 12 439.2 36.6summary(aov.ms.100) # ANOVA tábla, 100 ms ## Df Sum Sq Mean Sq F value Pr(>F)
## terulet 2 363.3 181.67 7.171 0.00894
## Residuals 12 304.0 25.33summary(aov.ms.150) # ANOVA tábla, 150 ms## Df Sum Sq Mean Sq F value Pr(>F)
## terulet 2 6.93 3.467 0.133 0.876
## Residuals 12 312.00 26.000TukeyHSD(aov.ms.50) # utóelemzés, 50 ms## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = ido ~ terulet, data = d.ms.50)
##
## $terulet
## diff lwr upr p adj
## A.terulet-Semleges -11.8 -22.007847 -1.592153 0.0238502
## B.terulet-Semleges -4.2 -14.407847 6.007847 0.5334091
## B.terulet-A.terulet 7.6 -2.607847 17.807847 0.1579954TukeyHSD(aov.ms.100) # utóelemzés, 100 ms ## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = ido ~ terulet, data = d.ms.100)
##
## $terulet
## diff lwr upr p adj
## A.terulet-Semleges -5 -13.49258 3.492583 0.2950432
## B.terulet-Semleges -12 -20.49258 -3.507417 0.0069733
## B.terulet-A.terulet -7 -15.49258 1.492583 0.1117572Az egyszerű hatások vizsgálatából arra következtethetünk, hogy a 150 ms-os várakozási idő esetén nincs különbség a terület faktor által meghatározott csoportok időre vonatkozó várható értékei között (\(F(2,12)=0,133;p=0,876\)), míg a másik két terület csoport esetén az egyszempontos varianciaelemzés szignifikánsnak bizonyult(50 ms-os várakozási idő esetén: \(F(2,12)=4,887;p=0,028\), 100 ms-os várakozási idő esetén: \(F(2,12)=7,171;p=0,009\)). A végrehajtott Tukey-próbákból továbbá kiderül, hogy az 50 ms-os esetben a Semleges és az A terület közötti különbség (\(p=0,024\)), a 100 ms-os esetben Semleges és B terület közötti különbség szignifikáns (\(p=0,007\)).
Alternatíva kétszempontos varianciaelemzésre.
library(lessR)
ANOVA(my.formula = ido ~ terulet * varakozasi.ido, data = d)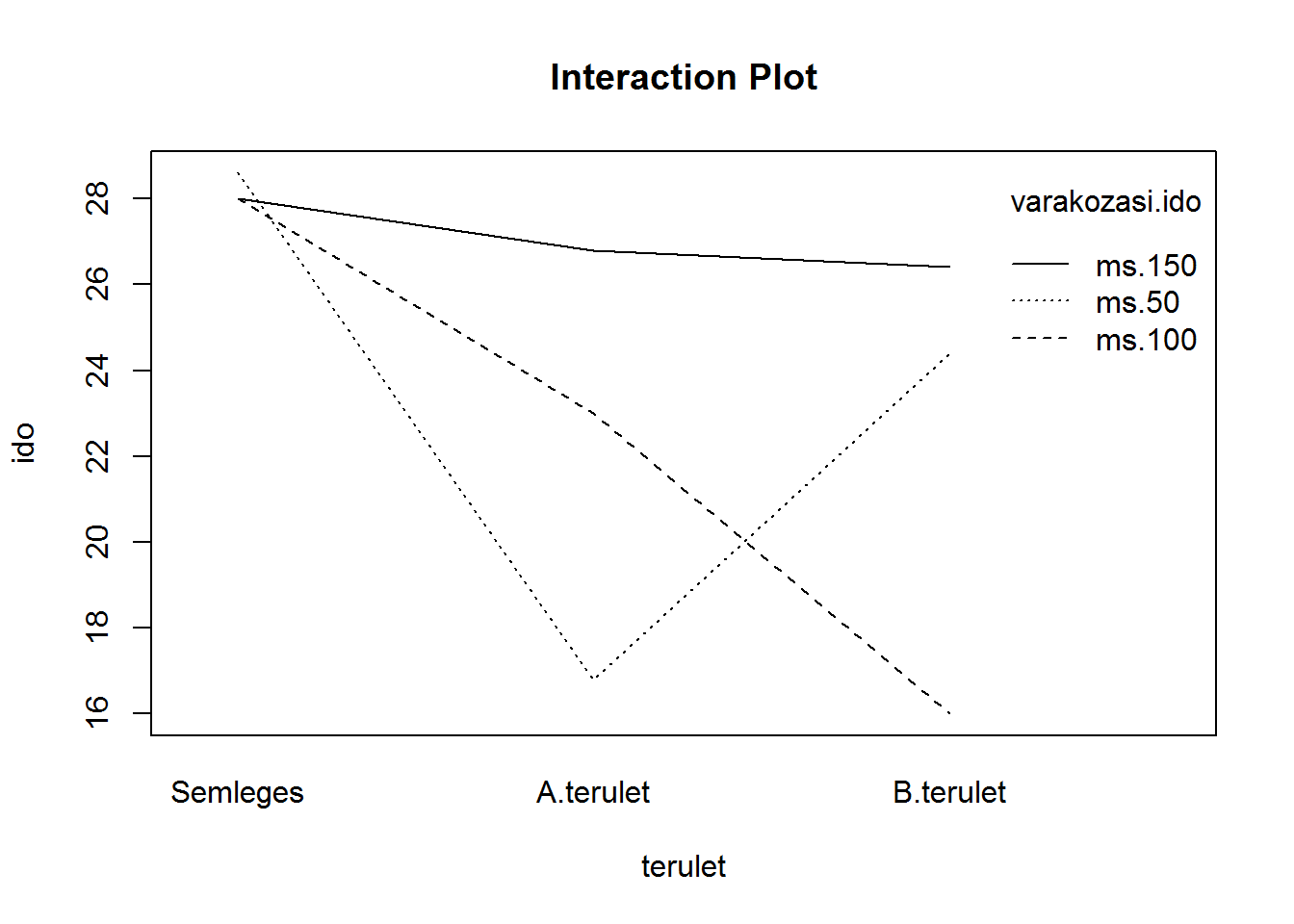
## BACKGROUND
##
## Response Variable: ido
##
## Factor Variable 1: terulet
## Levels: Semleges A.terulet B.terulet
##
## Factor Variable 2: varakozasi.ido
## Levels: ms.50 ms.100 ms.150
##
## Number of cases (rows) of data: 45
## Number of cases retained for analysis: 45
##
## The design is balanced
##
## Two-way Between Groups ANOVA
##
##
## DESCRIPTIVE STATISTICS
##
## Cell Sample Size: 5
##
##
## terulet
## varakozasi.ido Semleges A.terulet B.terulet
## ms.50 28.60 16.80 24.40
## ms.100 28.00 23.00 16.00
## ms.150 28.00 26.80 26.40
##
##
## terulet
## --------------------------------
## Semleges A.terulet B.terulet
## 1 28.20 22.20 22.27
##
## varakozasi.ido
## -----------------------
## ms.50 ms.100 ms.150
## 1 23.27 22.33 27.07
##
##
## 24.222
##
##
## terulet
## varakozasi.ido Semleges A.terulet B.terulet
## ms.50 7.40 5.72 4.72
## ms.100 4.69 4.74 5.61
## ms.150 5.61 5.40 4.16
##
##
## BASIC ANALYSIS
##
## df Sum Sq Mean Sq F-value p-value
## terulet 2 356.04 178.02 6.07 0.0053
## varakozasi.ido 2 188.58 94.29 3.22 0.0518
## terulet:varakozasi.ido 4 371.96 92.99 3.17 0.0248
## Residuals 36 1055.20 29.31
##
##
## Partial Omega Squared for terulet: 0.18
## Partial Omega Squared for varakozasi.ido: 0.09
## Partial Omega Squared for terulet & varakozasi.ido: 0.16
##
## Cohen's f for terulet: 0.47
## Cohen's f for varakozasi.ido: 0.31
## Cohen's f for terulet_&_varakozasi.ido: 0.44
##
##
##
## Family-wise Confidence Level: 0.95
##
## Factor: terulet
## ----------------------------------------------
## diff lwr upr p adj
## A.terulet-Semleges -6.00 -10.83 -1.17 0.01
## B.terulet-Semleges -5.93 -10.77 -1.10 0.01
## B.terulet-A.terulet 0.07 -4.77 4.90 1.00
##
## Factor: varakozasi.ido
## --------------------------------------
## diff lwr upr p adj
## ms.100-ms.50 -0.93 -5.77 3.90 0.88
## ms.150-ms.50 3.80 -1.03 8.63 0.15
## ms.150-ms.100 4.73 -0.10 9.57 0.06
##
## Cell Means
## -------------------------------------------------------------
## diff lwr upr p adj
## A.terulet:ms.50-Semleges:ms.50 -11.80 -23.09 -0.51 0.03
## B.terulet:ms.50-Semleges:ms.50 -4.20 -15.49 7.09 0.95
## Semleges:ms.100-Semleges:ms.50 -0.60 -11.89 10.69 1.00
## A.terulet:ms.100-Semleges:ms.50 -5.60 -16.89 5.69 0.78
## B.terulet:ms.100-Semleges:ms.50 -12.60 -23.89 -1.31 0.02
## Semleges:ms.150-Semleges:ms.50 -0.60 -11.89 10.69 1.00
## A.terulet:ms.150-Semleges:ms.50 -1.80 -13.09 9.49 1.00
## B.terulet:ms.150-Semleges:ms.50 -2.20 -13.49 9.09 1.00
## B.terulet:ms.50-A.terulet:ms.50 7.60 -3.69 18.89 0.42
## Semleges:ms.100-A.terulet:ms.50 11.20 -0.09 22.49 0.05
## A.terulet:ms.100-A.terulet:ms.50 6.20 -5.09 17.49 0.68
## B.terulet:ms.100-A.terulet:ms.50 -0.80 -12.09 10.49 1.00
## Semleges:ms.150-A.terulet:ms.50 11.20 -0.09 22.49 0.05
## A.terulet:ms.150-A.terulet:ms.50 10.00 -1.29 21.29 0.12
## B.terulet:ms.150-A.terulet:ms.50 9.60 -1.69 20.89 0.15
## Semleges:ms.100-B.terulet:ms.50 3.60 -7.69 14.89 0.98
## A.terulet:ms.100-B.terulet:ms.50 -1.40 -12.69 9.89 1.00
## B.terulet:ms.100-B.terulet:ms.50 -8.40 -19.69 2.89 0.29
## Semleges:ms.150-B.terulet:ms.50 3.60 -7.69 14.89 0.98
## A.terulet:ms.150-B.terulet:ms.50 2.40 -8.89 13.69 1.00
## B.terulet:ms.150-B.terulet:ms.50 2.00 -9.29 13.29 1.00
## A.terulet:ms.100-Semleges:ms.100 -5.00 -16.29 6.29 0.87
## B.terulet:ms.100-Semleges:ms.100 -12.00 -23.29 -0.71 0.03
## Semleges:ms.150-Semleges:ms.100 0.00 -11.29 11.29 1.00
## A.terulet:ms.150-Semleges:ms.100 -1.20 -12.49 10.09 1.00
## B.terulet:ms.150-Semleges:ms.100 -1.60 -12.89 9.69 1.00
## B.terulet:ms.100-A.terulet:ms.100 -7.00 -18.29 4.29 0.52
## Semleges:ms.150-A.terulet:ms.100 5.00 -6.29 16.29 0.87
## A.terulet:ms.150-A.terulet:ms.100 3.80 -7.49 15.09 0.97
## B.terulet:ms.150-A.terulet:ms.100 3.40 -7.89 14.69 0.98
## Semleges:ms.150-B.terulet:ms.100 12.00 0.71 23.29 0.03
## A.terulet:ms.150-B.terulet:ms.100 10.80 -0.49 22.09 0.07
## B.terulet:ms.150-B.terulet:ms.100 10.40 -0.89 21.69 0.09
## A.terulet:ms.150-Semleges:ms.150 -1.20 -12.49 10.09 1.00
## B.terulet:ms.150-Semleges:ms.150 -1.60 -12.89 9.69 1.00
## B.terulet:ms.150-A.terulet:ms.150 -0.40 -11.69 10.89 1.00
##
##
## RESIDUALS
##
## Fitted Values, Residuals, Standardized Residuals
## [sorted by Standardized Residuals, ignoring + or - sign]
## [res.rows = 20, out of 45 cases (rows) of data, or res.rows="all"]
## -----------------------------------------------------------
## terulet varakozasi.ido ido fitted residual z-resid
## 4 Semleges ms.50 40 28.60 11.40 2.35
## 18 A.terulet ms.50 26 16.80 9.20 1.90
## 5 Semleges ms.50 20 28.60 -8.60 -1.78
## 28 A.terulet ms.150 35 26.80 8.20 1.69
## 14 Semleges ms.150 20 28.00 -8.00 -1.65
## 21 A.terulet ms.100 31 23.00 8.00 1.65
## 37 B.terulet ms.100 24 16.00 8.00 1.65
## 15 Semleges ms.150 35 28.00 7.00 1.45
## 38 B.terulet ms.100 9 16.00 -7.00 -1.45
## 9 Semleges ms.100 35 28.00 7.00 1.45
## 33 B.terulet ms.50 18 24.40 -6.40 -1.32
## 16 A.terulet ms.50 11 16.80 -5.80 -1.20
## 30 A.terulet ms.150 21 26.80 -5.80 -1.20
## 32 B.terulet ms.50 30 24.40 5.60 1.16
## 42 B.terulet ms.150 21 26.40 -5.40 -1.12
## 10 Semleges ms.100 23 28.00 -5.00 -1.03
## 25 A.terulet ms.100 19 23.00 -4.00 -0.83
## 26 A.terulet ms.150 23 26.80 -3.80 -0.78
## 1 Semleges ms.50 25 28.60 -3.60 -0.74
## 34 B.terulet ms.50 28 24.40 3.60 0.74