7 Regresszióelemzés
A statisztikai modell egy egyenlet, amely függő változó értékeit magyarázza független változók és paraméterek segítségével:
\[\text{függő változó = modell + hiba}\]
A statisztikai modell egy hibatagot is tartalmaz, amely a függő változó modell által nem magyarázott részéért felelős.
Az R-ben a statisztikai modellt egy tilde (~) karaktert tartalmazó formula segítségével írjuk le, és elegendő a függő változót és a modellt megadni, a hibatagot automatikusan hozzáfűződik a formulához.
\[\text{függő változó ~ modell}\]
A következő táblázatban a legegyszerűbb statisztikai modelleket soroljuk fel. A függő változót y jelöli, a független folytonos változókat x, x1, x2 stb., a független faktor változókat A, B stb. A hibatagot az \(\varepsilon\) képviseli a statisztikai modellben.
| Statisztikai modell | R modell formula | Leírás |
|---|---|---|
| \(y_i=\beta_0+\varepsilon_i\) | y ~ 1 |
Egyszerű lineáris regresszió csak a tengelymetszettel |
| \(y_i=\beta_1 x_i+\varepsilon_i\) | y ~ x - 1 |
Egyszerű lineáris regresszió tengelymetszet nélkül |
| \(y_i=\beta_0+\beta_1 x_i+\varepsilon_i\) | y ~ x (vagy y ~ x + 1) |
Egyszerű lineáris regresszió |
| \(y_i=\beta_0+\beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_r x_{ir} +\varepsilon_i\) | y ~ x1 + x2 + ... + xr |
Többszörös lineáris regresszió |
| \(y_{ij}=\mu+\alpha_i+\varepsilon_{ij}\) | y ~ A |
Egyszempontos varianciaelemzés |
| \(y_{ijk}=\mu+\alpha_i+\beta_j+\varepsilon_{ijk}\) | y ~ A + B |
Kétszempontos varianciaelemzés interakció nélkül |
| \(y_{ijk}=\mu+\alpha_i+\beta_j+\alpha_i \beta_j+\varepsilon_{ijk}\) | y ~ A * B |
Kétszempontos varianciaelemzés |
7.1 Egyszerű lineáris regresszió
Az egyszerű lineáris regresszió a folytonos \(Y\) függő változó és a folytonos \(X\) magyarázó változó között keresi a lineáris kapcsolat formáját: \(y_i=\beta_0+\beta_1 x_i+\varepsilon_i\). A populációbeli \(\beta_0\) tengelymetszet és \(\beta_1\) meredekség a minta alapján kerül becslésre, ezeket \(b_0\) és \(b_1\) jelöli.
Alkalmazási feltételek:
- lineáris kapcsolat a folytonos
XésYközött - a reziduumok (\(\varepsilon_i\)) függetlenek és normális eloszlásúak, 0 várható értékkel állandó szórással: \(\varepsilon_i \sim N(0,\sigma)\)
Null- és ellenhipotézisek:
- A tengelymetszetre:
- Nullhipotézis:
- \(H_0:\beta_0=0\)
- Ellenhipotézis:
- \(H_1:\beta_0 \neq 0\)
- Nullhipotézis:
- A meredekségre:
- Nullhipotézis:
- \(H_0:\beta_1=0\)
- Ellenhipotézis:
- \(H_1:\beta_1 \neq 0\)
- Nullhipotézis:
- A teljes modellre:
- Nullhipotézis:
- \(H_0:\) Az \(Y\) változó függ \(X\)-től
- Ellenhipotézis:
- \(H_1:\) Az \(Y\) változó nem függ \(X\)-től
- Nullhipotézis:
Próbastatisztika:
Az együtthatók becslése:
\[b_1=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i-\bar{x})^2}=\frac{s_{xy}}{s_x^2}=r\frac{s_y}{s_x}\]
\[b_0=\bar{y}-b_1\bar{x}\]
A hibatag standard hibája (residual standard error):
\[SE_e=\sqrt{\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{(n-2)}}\]
A paraméterbecslések standard hibája:
\[SE_{b_1}=\frac{SE_e}{\sqrt{\sum_{i=1}^n(x_i-\bar{x}_i)^2}}\]
\[SE_{b_0}=SE_e\sqrt{\frac{\sum_{i=1}^nx_i^2}{n\sum_{i=1}^n(x_i-\bar{x}_i)^2}}\]
A próbastatisztika a két paraméterre:
\[T_{\beta_0}=\frac{b_0}{SE_{b_0}} \sim t(n-2)\] \[T_{\beta_1}=\frac{b_1}{SE_{b_1}} \sim t(n-2)\]
Az \(Y\) teljes szórása \(SS_Y\) (SS - sum of squares, eltérés négyzetösszeg), az \(X\)-től való függésből eredő szórás \(SS_R\), a véletlen hiba \(SS_H\):
\[SS_T=\sum_{i=1}^n(y_i-\bar{y})^2, SS_R=\sum_{i=1}^n(\hat{y}_i-\bar{y})^2, SS_H=\sum_{i=1}^n(y_i-\hat{y}_i)^2\]
A próbastatisztika a teljes modellre:
\[F=\frac{SS_R}{SS_H/(n-2)} \sim F(1,n-2)\]
7.1.1 Példa: öngyilkosságok száma és a GDP
Vizsgáljuk meg, hogy a szegényebb országokban valóban gyakoribbak-e a deviáns viselkedések (most az öngyilkosságok). Az adatbázisban 100 ország GDP-je (
GDPváltozó) és a 100 ezer lakosra jutó öngyilkosságok száma szerepel (ONGYILK).
Forrás: (Moksony 2006, 51), http://www.bkae.hu/moksony
Adatok beolvasása. Olvassuk be az adatokat egy d nevű adattáblába:
d <- read.table(file = textConnection("
ONGYILK GDP
15,4808452962898 1592
47,0141940186732 1410
29,0007875217125 1773
25,1129959323443 1548
27,7497949949466 1683
9,6539463638328 1766
43,9136226396077 1558
23,1701795114204 1237
18,7472061612643 1640
18,8921054950915 1342
46,1234088438563 2385
21,4419082115404 2754
35,094865800906 2655
11,3840771523304 2766
29,7233101521619 2565
39,8356329697184 2666
15,6394705484621 2566
38,8877468724735 2497
19,1461172309704 2234
22,4131288920529 2559
29,9858853229322 3763
19,0991911691614 3345
34,6698938923888 3528
23,6689220237546 3384
43,1926002366468 3366
18,9651394494809 3432
26,1203125518747 3633
40,5877505856566 3267
33,9038489627652 3718
51,0089286429807 3527
18,5364534274675 4504
37,6291882351041 4474
33,2144021025859 4338
33,9969320932403 4516
48,3692275837064 4768
12,5400950328447 4574
33,6396538570523 4606
33,011191279348 4666
34,6337022224441 4766
46,8798595026136 4523
32,7210248406045 5772
59,3739377115853 5299
36,3754091402516 5669
36,382358783856 5369
20,1428669295274 5742
28,5156811471097 5343
47,6564468001015 5383
32,4720279118046 5778
41,2753857318312 5436
32,8877597651445 5255
50,6552498091944 6381
37,546302987542 6608
37,8844092896208 6673
54,3332683828659 6709
23,1775315998122 6448
52,6364162613638 6781
32,429948760476 6439
40,8286790659651 6444
58,1353630957193 6372
33,1451081035659 6712
45,8986729705706 7608
58,3343449235894 7410
23,0541208857671 7701
41,6460095877759 7748
37,04256635122 7283
50,0429612720385 7708
63,1047336385586 7294
32,2589312741533 7282
39,9371174509637 7359
44,2498992007226 7239
31,7986775579862 8560
38,8693911744282 8465
59,4397788661532 8344
46,3058306206018 8716
35,4286840836518 8490
40,0737322512082 8777
37,2537268115208 8558
67,2846841233782 8311
46,1897647403181 8334
32,3759523312561 8274
47,3710529368371 9538
44,9487500383519 9531
59,0558021903969 9414
46,6849101127125 9797
30,6582923887298 9751
51,956861750409 9640
47,3536566390656 9320
61,9958981961943 9707
52,2816479743458 9437
25,928241407685 9383
35,6244308524765 10487
50,5871581011452 10287
69,1737026707269 10665
47,8075659652241 10447
46,634703474585 10315
30,8032587342896 10732
54,2931397729553 10688
56,8695374266244 10799
49,4638912756927 10334
46,3957459577359 10637
"), header=T, sep="", dec = ",")
str(d) # az adattábla szerkezete## 'data.frame': 100 obs. of 2 variables:
## $ ONGYILK: num 15.5 47 29 25.1 27.7 ...
## $ GDP : int 1592 1410 1773 1548 1683 1766 1558 1237 1640 1342 ...d # a beolvasott adattábla## ONGYILK GDP
## 1 15.480845 1592
## 2 47.014194 1410
## 3 29.000788 1773
## 4 25.112996 1548
## 5 27.749795 1683
## 6 9.653946 1766
## 7 43.913623 1558
## 8 23.170180 1237
## 9 18.747206 1640
## 10 18.892105 1342
## 11 46.123409 2385
## 12 21.441908 2754
## 13 35.094866 2655
## 14 11.384077 2766
## 15 29.723310 2565
## 16 39.835633 2666
## 17 15.639471 2566
## 18 38.887747 2497
## 19 19.146117 2234
## 20 22.413129 2559
## 21 29.985885 3763
## 22 19.099191 3345
## 23 34.669894 3528
## 24 23.668922 3384
## 25 43.192600 3366
## 26 18.965139 3432
## 27 26.120313 3633
## 28 40.587751 3267
## 29 33.903849 3718
## 30 51.008929 3527
## 31 18.536453 4504
## 32 37.629188 4474
## 33 33.214402 4338
## 34 33.996932 4516
## 35 48.369228 4768
## 36 12.540095 4574
## 37 33.639654 4606
## 38 33.011191 4666
## 39 34.633702 4766
## 40 46.879860 4523
## 41 32.721025 5772
## 42 59.373938 5299
## 43 36.375409 5669
## 44 36.382359 5369
## 45 20.142867 5742
## 46 28.515681 5343
## 47 47.656447 5383
## 48 32.472028 5778
## 49 41.275386 5436
## 50 32.887760 5255
## 51 50.655250 6381
## 52 37.546303 6608
## 53 37.884409 6673
## 54 54.333268 6709
## 55 23.177532 6448
## 56 52.636416 6781
## 57 32.429949 6439
## 58 40.828679 6444
## 59 58.135363 6372
## 60 33.145108 6712
## 61 45.898673 7608
## 62 58.334345 7410
## 63 23.054121 7701
## 64 41.646010 7748
## 65 37.042566 7283
## 66 50.042961 7708
## 67 63.104734 7294
## 68 32.258931 7282
## 69 39.937117 7359
## 70 44.249899 7239
## 71 31.798678 8560
## 72 38.869391 8465
## 73 59.439779 8344
## 74 46.305831 8716
## 75 35.428684 8490
## 76 40.073732 8777
## 77 37.253727 8558
## 78 67.284684 8311
## 79 46.189765 8334
## 80 32.375952 8274
## 81 47.371053 9538
## 82 44.948750 9531
## 83 59.055802 9414
## 84 46.684910 9797
## 85 30.658292 9751
## 86 51.956862 9640
## 87 47.353657 9320
## 88 61.995898 9707
## 89 52.281648 9437
## 90 25.928241 9383
## 91 35.624431 10487
## 92 50.587158 10287
## 93 69.173703 10665
## 94 47.807566 10447
## 95 46.634703 10315
## 96 30.803259 10732
## 97 54.293140 10688
## 98 56.869537 10799
## 99 49.463891 10334
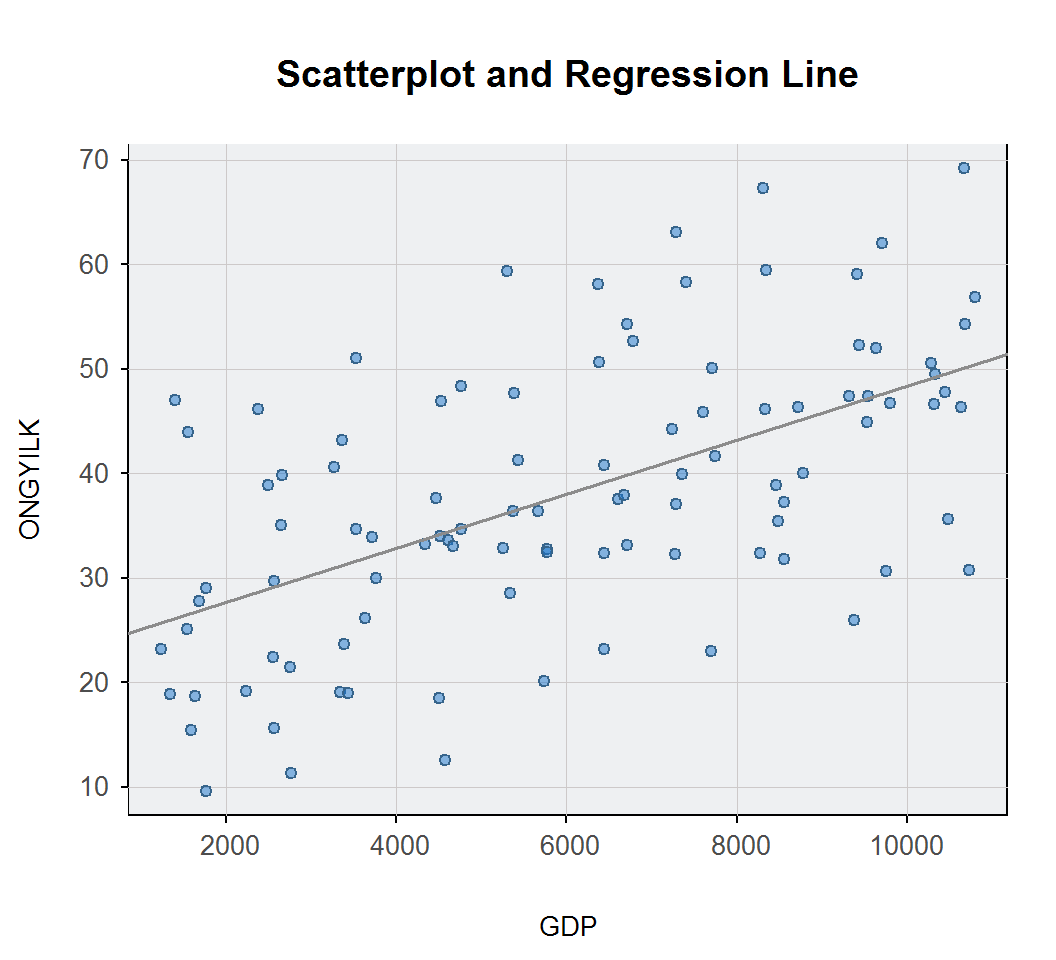
## 100 46.395746 10637Grafikus ábrázolás két kvantitatív változó kapcsolatára. Kétdimenziós pontdiagram segítségével ábrázoljuk a két változó kapcsolatát. Vizsgáljuk meg, hogy a két változó között a lineáris kapcsolat feltételezését az adatok alátámasztják-e!
A ggplot2 csomag segítségével a kétdimenziós pontdiagramot (geom_point()), és a regressziós egyenest a 95%-os konfidencia sávval (geom_smooth(method=lm)) is megrajzolhatjuk.
library(ggplot2)
ggplot(data = d, mapping = aes(x = GDP, y = ONGYILK)) +
geom_point(size=4, colour = "blue", alpha = 0.6, shape=21, fill="grey") + theme_bw() +
geom_smooth(method=lm)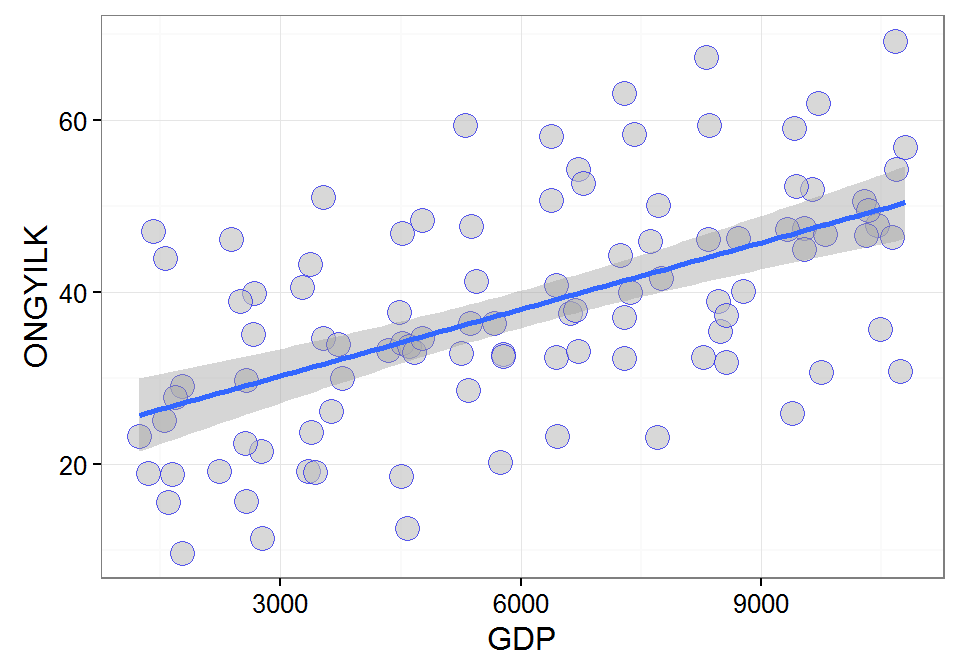
A car csomag scatterplot() függvényével is elkészíthetjük a szórásdiagramot. A margókon a változók dobozdiagramja is megjelenik, valamint a regressziós egyenesen túl, illesztett nemlineáris görbét is kapunk. A zöld színű regressziós egyenes és a piros görbe átfedéséből a két változó lineáris kapcsolatára tudunk következtetni.
library(car)
scatterplot(x = d$GDP, y = d$ONGYILK, spread = F)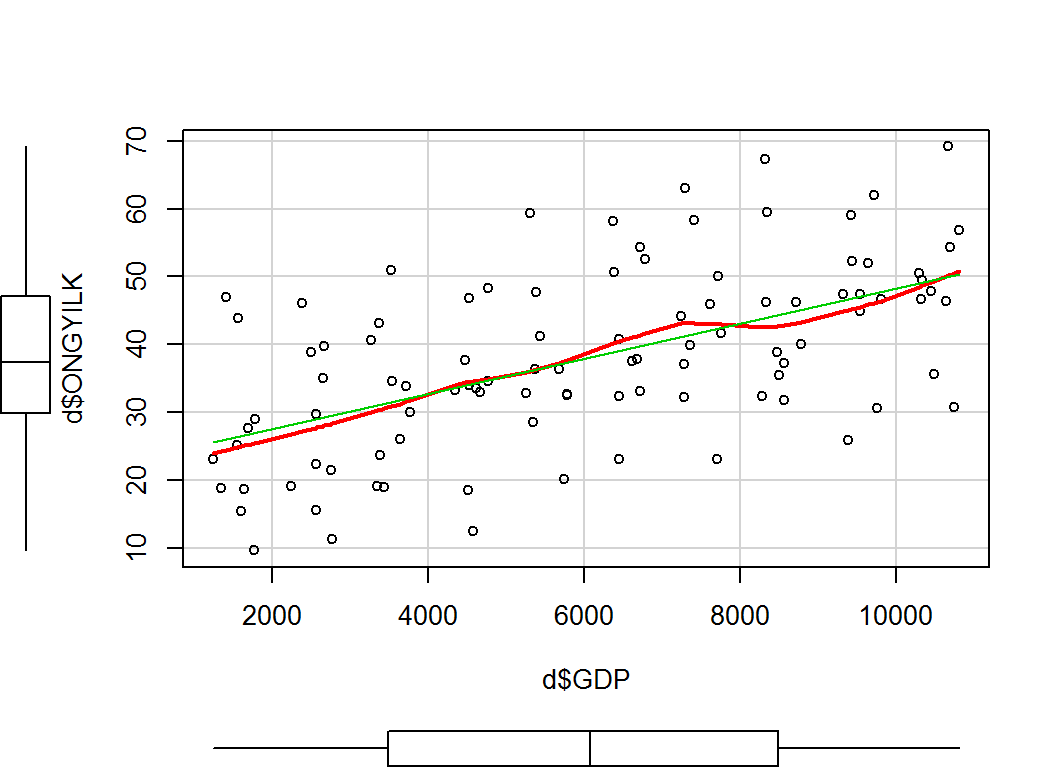
A lessR csomag ScatterPlot() függvényével adott valószínűségű adatellipszist rajzolhatunk (a 95%-os adatellipszishez használjuk az ellipse=0.95 argumentumot). A fit.line="ls" argumentummal a regressziós egyenest is berajzolhatjuk.
library(lessR)
ScatterPlot(x = GDP, y = ONGYILK, data = d, ellipse = 0.95, fit.line = "ls")## [Ellipse with Murdoch and Chow's function ellipse from the ellipse package]
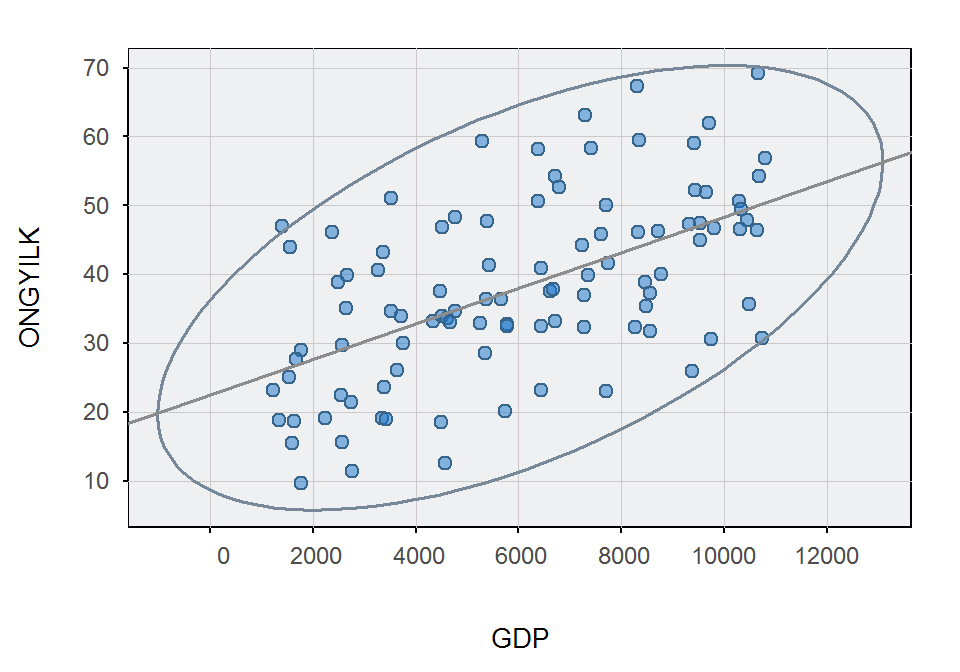
##
## >>> Pearson's product-moment correlation
##
## Number of paired values with neither missing, n = 100
##
##
## Sample Correlation of GDP and ONGYILK: r = 0.565
##
##
## Alternative Hypothesis: True correlation is not equal to 0
## t-value: 6.780, df: 98, p-value: 0.000
##
## 95% Confidence Interval of Population Correlation
## Lower Bound: 0.415 Upper Bound: 0.685A fenti ábrákról leolvasható, hogy a lineáris kapcsolat feltételezhető. Keressük meg a kapcsolat formáját!
Az egyszerű lineáris regresszió végrehajtása. A kétdimenziós pontdiagram (szórásdiagram) a két változó kapcsolatának fő vonásait feltárta, de ha egyetlen görbébe szeretnénk sűríteni a két változó átlagos összefüggését, akkor a regressziószámítást kell végeznünk. Egyszerű lineáris regressziót az lm() függvénnyel hajunk végre, ahol a statisztikai modell megadásához esetünkben a formula = ONGYILK ~ GDP argumentumot kell megadni.
# a lineáris modell illesztése, modellobjektum létrehozása
lm.1 <- lm(formula = ONGYILK ~ GDP, data = d)
summary(lm.1) # hipotézisvizsgálat a regressziós paraméterekre és a teljes modellre##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.7691 -7.1339 -0.7589 5.9267 23.3114
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.4807127 2.5462232 8.829 4.19e-14
## GDP 0.0025860 0.0003814 6.780 9.09e-10
##
## Residual standard error: 10.94 on 98 degrees of freedom
## Multiple R-squared: 0.3193, Adjusted R-squared: 0.3124
## F-statistic: 45.97 on 1 and 98 DF, p-value: 0.0000000009095library(lsr)
standardCoefs(lm.1) # standardizált regressziós paraméterek## b beta
## GDP 0.002586034 0.5650759confint(object = lm.1, level = 0.95) # konfidenciaintarvallumok a regressziós paraméterekre## 2.5 % 97.5 %
## (Intercept) 17.427815611 27.533609778
## GDP 0.001829144 0.003342924Az egyszerű lineáris regresszió értékelése. Lineáris regressziót hajtottunk végre, hogy megvizsgáljuk a GDP hatását az öngyilkossági ráta alakulására. A GDP 1 dolláros emelkedése esetén az öngyilkossági arány átlagosan 0,0026-del nő (\(F(1, 98)=45,97; p < 0.0001\)). A meredekségre vonatkozó konfidenciaintervallum \(\left]0,0018; 0,0033\right[\), a reziduális szórás (vagyis a regressziós becslés standard hibája) pedig 10,94. Az \(R^2=0,32\), ami azt mutatja, hogy a GDP mindössze 32%-ot magyaráz meg az öngyilkossági ráta ingadozásából.
Predikció az egyszerű lineáris regresszióban. Az egyszerű lineáris regresszió elvégzése után láthatjuk a regressziós egyenes két paraméterének becslését, \(b_0=22,481\) és \(b_1=0,0026\). Ezek alapján felírható a regressziós egyenes egyenlete:
\[\hat{Y}=22,481 + 0,0026 \times X\]
azaz
\[\text{Becsült öngyilkossági arány} = 22,481 + 0,0026 \times \text{GDP}\]
A \(b_0=22,481\) tengelymetszet jelentése: az öngyilkossági arány becsült átlagos értéke, amikor a GDP értéke 0. A \(b_1=0,0026\) meredekség jelentése: a GDP 1 dolláros emelkedése esetén az öngyilkossági arány átlagosan 0,0026-del nő.
A regressziós egyenes együtthatóit máris kihasználhatjuk előrejelzésre, azaz tetszőleges GDP értékhez meghatározhatjuk a becsült öngyilkossági arány mértékét. Egy szegény (\(GDP=2000\)) és egy gazdag (\(GDP=10000\)) ország öngyilkossági arányára kérünk előrejelzést. A predikcióhoz a predict() függvényt használjuk:
d.pred <- data.frame(GDP=c(2000, 10000)) # adatok előkészítése a predikcióhoz
predict(object = lm.1, newdata = d.pred) # előrejelzés az egyszerű lineáris regresszió alapján## 1 2
## 27.65278 48.34105A fenti output alapján a becsült öngyilkossági arány 27,65, illetve 48,34, abban a két országban, ahol a GDP 2000, illetve 10000 dollár.
A mintabeli \(X\) magyarázó változó összes értékére is megkaphatjuk a becsült \(\hat{Y}\) értékeket a fitted() függvény segítségével. Ha megjelenítjük a magyarázó változó \(x_i\) és a függő változó becsült \(\hat{y}_i\) értékeit, akkor a regressziós egyenes pontjait kapjuk vissza.
print(fitted(lm.1), digits = 5) # a jósolt Y pontok, az egyenes Y pontjai## 1 2 3 4 5 6 7 8 9 10
## 26.598 26.127 27.066 26.484 26.833 27.048 26.510 25.680 26.722 25.951
## 11 12 13 14 15 16 17 18 19 20
## 28.648 29.603 29.347 29.634 29.114 29.375 29.116 28.938 28.258 29.098
## 21 22 23 24 25 26 27 28 29 30
## 32.212 31.131 31.604 31.232 31.185 31.356 31.876 30.929 32.096 31.602
## 31 32 33 34 35 36 37 38 39 40
## 34.128 34.051 33.699 34.159 34.811 34.309 34.392 34.547 34.806 34.177
## 41 42 43 44 45 46 47 48 49 50
## 37.407 36.184 37.141 36.365 37.330 36.298 36.401 37.423 36.538 36.070
## 51 52 53 54 55 56 57 58 59 60
## 38.982 39.569 39.737 39.830 39.155 40.017 39.132 39.145 38.959 39.838
## 61 62 63 64 65 66 67 68 69 70
## 42.155 41.643 42.396 42.517 41.315 42.414 41.343 41.312 41.511 41.201
## 71 72 73 74 75 76 77 78 79 80
## 44.617 44.371 44.059 45.021 44.436 45.178 44.612 43.973 44.033 43.878
## 81 82 83 84 85 86 87 88 89 90
## 47.146 47.128 46.826 47.816 47.697 47.410 46.583 47.583 46.885 46.745
## 91 92 93 94 95 96 97 98 99 100
## 49.600 49.083 50.061 49.497 49.156 50.234 50.120 50.407 49.205 49.988plot(d$GDP, fitted(lm.1)) # a megjelenített pontok a regressziós egyenesre illeszkednek
Konfidencia-sáv, predikciós-sáv és tolarencia-sáv. Az együtthatókra adott fenti lehetséges értékekkel megrajzolt regressziós egyenesek egy konfidencia-sávot adnak. A konfidencia-sáv a valódi egyenes minden pontját adott valószínűséggel tartalmazza.
A predikciós-sáv egyedi \(Y\) megfigyelésekre ad intervallumbecslést adott \(X\) értékek esetén. A predikciós-sáv olyan \(X\)-től függő intervallumot szolgáltat, amely adott valószínűséggel tartalmazza az \(X\)-hez tartozó, új \(Y\) megfigyelést. Példál 95% lehet a valószínűsége annak, hogy adott \(X\) értéknél egy későbbi mérés eredménye a predikciós intervallumba esik.
d.pred <- data.frame(GDP=seq(from=min(d$GDP, na.rm = T), to = max(d$GDP, na.rm = T), by=100))
plot(x = d$GDP, y = d$ONGYILK)
lm.1.pred <- predict(object = lm.1, newdata = d.pred, int = "confidence") # konfidencia-sáv
matlines(x = d.pred$GDP, y = lm.1.pred[,1])
matlines(x = d.pred$GDP, y = lm.1.pred[,2])
matlines(x = d.pred$GDP, y = lm.1.pred[,3])
lm.1.pred <- predict(object = lm.1, newdata = d.pred, int = "prediction") # predikciós-sáv
matlines(x = d.pred$GDP, y = lm.1.pred[,1])
matlines(x = d.pred$GDP, y = lm.1.pred[,2])
matlines(x = d.pred$GDP, y = lm.1.pred[,3])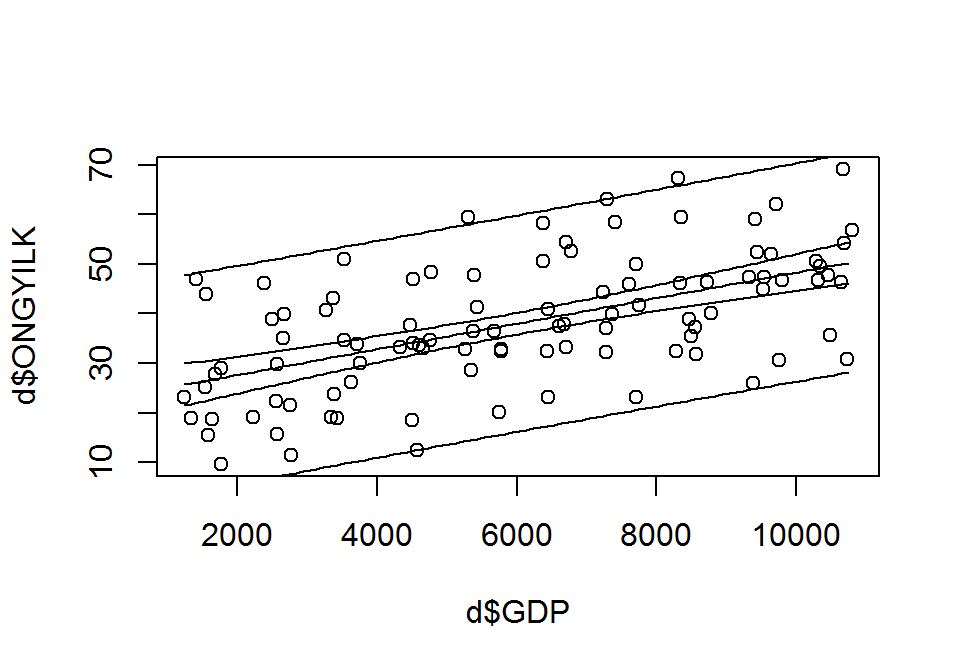
A tolerancia-sáv megrajzolása:
# tolerancia-sáv megrajzolása
library("tolerance")
lm.1.pred <- regtol.int(reg = lm.1, new.x = d.pred$GDP, alpha = 0.05, P = 0.95, side = 2)
plottol(lm.1.pred, x = cbind(1, d$GDP), y = d$ONGYILK, side = "two", x.lab = "X", y.lab = "Y")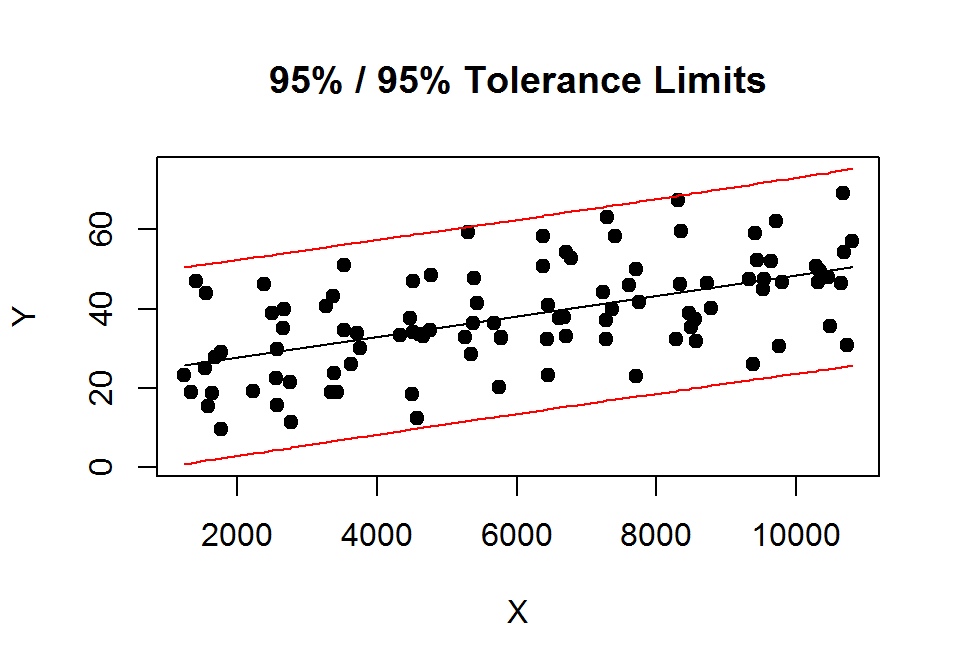
# https://repozitorium.omikk.bme.hu/bitstream/handle/10890/1048/ertekezes.pdf?sequence=1
# http://www.graphpad.com/support/faqid/1506/A regressziós diagnosztikán a regresszió során kapott eredmények vizsgálatát értjük (az illesztett modell jóságának vizsgálata, a torzító pontok keresése és az alkalmazási feltételek vizsgálata). A regressziós diagnosztika jórészt a reziduumok elemzéséből áll, így először ezeket mutatjuk be.
A reziduumok formái. A regresszió végrehajtása után a számos függvényt alkalmazhatunk a lineáris modell által visszaadott objektumra (most az lm.1 objektumra). Ilyen volt a már korábban látott summary() vagy fitted() függvény is, de a reziduumok 3 különböző formáját (nem standardizált, standardizált és studentizált) szolgáltató függvények is ilyenek.
A residuals() függvény az \(e_i=y_i-\hat{y}_i\) közönséges (nem standardizált) reziduumokat adja vissza, vagyis a megfigyelt \(y_i\) és az illesztett \(\hat{y}_i\) közötti távolságot szolgáltatja.
print(residuals(lm.1), digits = 3) # reziduumok## 1 2 3 4 5 6 7 8
## -11.1168 20.8872 1.9350 -1.3709 0.9168 -17.3937 17.4039 -2.5095
## 9 10 11 12 13 14 15 16
## -7.9746 -7.0591 17.4750 -8.1607 5.7482 -18.2496 0.6094 10.4606
## 17 18 19 20 21 22 23 24
## -13.4770 9.9497 -9.1118 -6.6852 -2.2261 -12.0318 3.0657 -7.5629
## 25 26 27 28 29 30 31 32
## 12.0073 -12.3908 -5.7555 9.6585 1.8083 19.4073 -15.5918 3.5786
## 33 34 35 36 37 38 39 40
## -0.4845 -0.1623 13.5583 -21.7691 -0.7523 -1.5360 -0.1720 12.7025
## 41 42 43 44 45 46 47 48
## -4.6863 23.1898 -0.7655 0.0172 -17.1869 -7.7822 11.2551 -4.9508
## 49 50 51 52 53 54 55 56
## 4.7370 -3.1826 11.6731 -2.0229 -1.8529 14.5029 -15.9779 12.6198
## 57 58 59 60 61 62 63 64
## -6.7022 1.6836 19.1764 -6.6931 3.7434 16.6911 -19.3416 -0.8713
## 65 66 67 68 69 70 71 72
## -4.2722 7.6291 21.7615 -9.0533 -1.5742 3.0489 -12.8185 -5.5021
## 73 74 75 76 77 78 79 80
## 15.3812 1.2852 -9.0075 -5.1046 -7.3583 23.3114 2.1570 -11.5016
## 81 82 83 84 85 86 87 88
## 0.2248 -2.1795 12.2302 -1.1312 -17.0388 4.5468 0.7711 14.4126
## 89 90 91 92 93 94 95 96
## 5.3965 -20.8172 -13.9760 1.5039 19.1129 -1.6894 -2.5209 -19.4308
## 97 98 99 100
## 4.1729 6.4622 0.2591 -3.5926plot(d$GDP, residuals(lm.1)) # maradékdiagram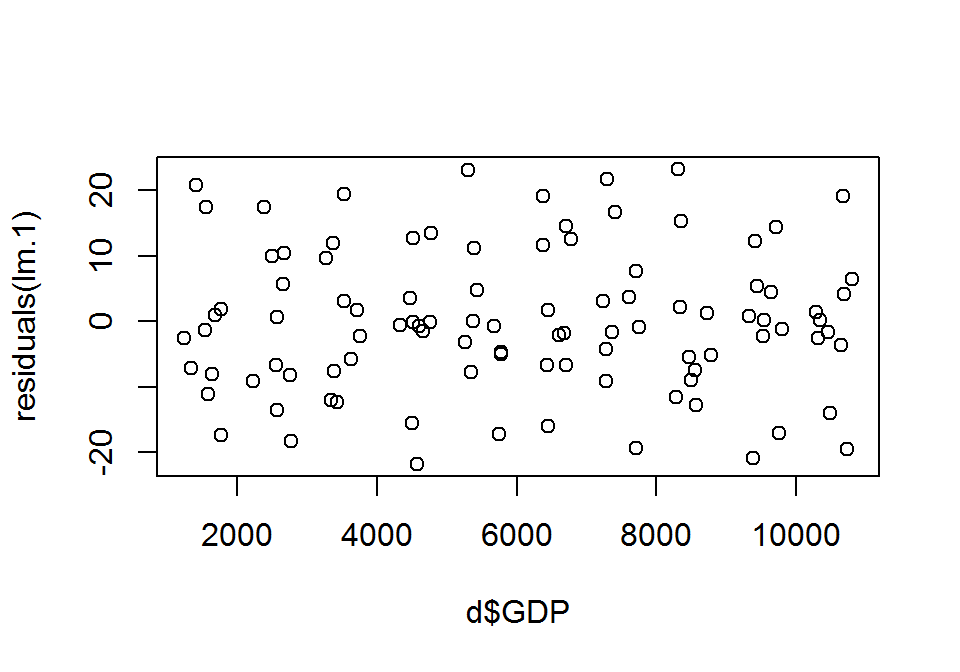
Az rstandard() függvény a standardizált reziduumokat szolgáltatja. A különböző regressziós modellek különböző szórású reziduumokat tartalmaznak (a várható értékek azonban nullák), így nem a konkrét reziduumok érdekelnek minket igazán, inkább azok mintázatai, a különösen nagy értékek előfordulása. A standardizált reziduumok az \(SE_e\) a standard hibával való osztással, vagyis normalizálással jönnek létre, szórásuk így 1-gyel egyenlő. Kiszámításuk: \(e_i^{'}=\frac{e_i}{SE_e\sqrt{1-h_i}}\), ahol \(h_i\) a hatóerő, amelynek fogalmát később közöljük.
print(rstandard(lm.1), digits = 3) # standardizált reziduumok## 1 2 3 4 5 6 7 8
## -1.03425 1.94525 0.17985 -0.12757 0.08525 -1.61668 1.61947 -0.23395
## 9 10 11 12 13 14 15 16
## -0.74172 -0.65768 1.61926 -0.75498 0.53201 -1.68826 0.05642 0.96810
## 17 18 19 20 21 22 23 24
## -1.24780 0.92149 -0.84491 -0.61899 -0.20523 -1.11068 0.28283 -0.69806
## 25 26 27 28 29 30 31 32
## 1.10834 -1.14350 -0.53082 0.89183 0.16673 1.79048 -1.43497 0.32937
## 33 34 35 36 37 38 39 40
## -0.04461 -0.01494 1.24726 -2.00325 -0.06923 -0.14132 -0.01583 1.16902
## 41 42 43 44 45 46 47 48
## -0.43070 2.13190 -0.07036 0.00158 -1.57960 -0.71541 1.03464 -0.45501
## 49 50 51 52 53 54 55 56
## 0.43544 -0.29259 1.07287 -0.18595 -0.17033 1.33323 -1.46857 1.16020
## 57 58 59 60 61 62 63 64
## -0.61602 0.15474 1.76249 -0.61529 0.34456 1.53576 -1.78061 -0.08022
## 65 66 67 68 69 70 71 72
## -0.39301 0.70235 2.00191 -0.83282 -0.14483 0.28045 -1.18272 -0.50751
## 73 74 75 76 77 78 79 80
## 1.41825 0.11865 -0.83091 -0.47132 -0.67892 2.14927 0.19889 -1.06032
## 81 82 83 84 85 86 87 88
## 0.02081 -0.20182 1.13198 -0.10488 -1.57941 0.42125 0.07134 1.33570
## 89 90 91 92 93 94 95 96
## 0.49953 -1.92652 -1.30041 0.13978 1.78019 -0.15716 -0.23434 -1.81051
## 97 98 99 100
## 0.38872 0.60238 0.02409 -0.33456plot(d$GDP, rstandard(lm.1)) # standardizált maradékdiagram
Az rstudent() függvény a studentizált reziduumokat (vagy jackknife reziduumokat) szolgáltatja. A studentizált reziduumok is normalizált reziduumnak számítanak, de egy módosított képletet alkalmazunk, melyben minden pontra úgy határozzuk meg reziduumot, mintha a regresszió során az adott pontot kihagynánk. A képletben szereplő \(e_{-i}=y_i-\hat{y}_{-i}\) és \(SE_{e_{-i}}\) az \(i.\) pont eltávolítása után kapott reziduumok és standard hibák. Kiszámítása: \(e_i^*=\frac{e_{(-i)}}{SE_{e_{-i}}\sqrt{1-h_i}}\)
print(rstudent(lm.1), digits = 3) # studentizált reziduumok## 1 2 3 4 5 6 7 8
## -1.03462 1.97378 0.17896 -0.12693 0.08482 -1.63029 1.63319 -0.23282
## 9 10 11 12 13 14 15 16
## -0.74000 -0.65577 1.63297 -0.75332 0.53006 -1.70460 0.05614 0.96779
## 17 18 19 20 21 22 23 24
## -1.25140 0.92078 -0.84366 -0.61703 -0.20422 -1.11202 0.28150 -0.69622
## 25 26 27 28 29 30 31 32
## 1.10965 -1.14531 -0.52886 0.89089 0.16590 1.81119 -1.44287 0.32787
## 33 34 35 36 37 38 39 40
## -0.04438 -0.01486 1.25085 -2.03510 -0.06887 -0.14061 -0.01575 1.17124
## 41 42 43 44 45 46 47 48
## -0.42890 2.17196 -0.07000 0.00158 -1.59191 -0.71362 1.03502 -0.45316
## 49 50 51 52 53 54 55 56
## 0.43363 -0.29122 1.07370 -0.18503 -0.16948 1.33860 -1.47741 1.16227
## 57 58 59 60 61 62 63 64
## -0.61406 0.15397 1.78195 -0.61332 0.34300 1.54663 -1.80087 -0.07981
## 65 66 67 68 69 70 71 72
## -0.39131 0.70052 2.03368 -0.83151 -0.14411 0.27913 -1.18516 -0.50558
## 73 74 75 76 77 78 79 80
## 1.42570 0.11805 -0.82958 -0.46944 -0.67704 2.19053 0.19791 -1.06100
## 81 82 83 84 85 86 87 88
## 0.02071 -0.20083 1.13363 -0.10435 -1.59172 0.41947 0.07098 1.34113
## 89 90 91 92 93 94 95 96
## 0.49761 -1.95402 -1.30507 0.13908 1.80044 -0.15638 -0.23321 -1.83215
## 97 98 99 100
## 0.38703 0.60041 0.02397 -0.33304plot(d$GDP, rstudent(lm.1))
Kiugró értékek, hatóerő és torzító pontok. A különösen nagy reziduumal rendelkező megfigyelések a kiugró értékek, vagyis amikor a megfigyelt érték és a becsült érték túlságosan távol esik egymástól. Kiugró pontok keresésére a legjobb a studentizált reziduumok vizsgálata, amelyek \(t(n-3)\) eloszlásúak, amennnyiben nincsenek kiugró értékek. Ezt kihasználva megkereshetjük az eloszlás választott pontjától (most 97,5%-os kvantilistől) nagyobb értékeket a mintában.
rstudent(lm.1)[abs(rstudent(lm.1)) > qt(p = 0.975, df = 97)]## 36 42 67 78
## -2.035103 2.171962 2.033685 2.190527Látható, hogy 4 ilyen érték van, de studentizált reziduum értékük nem sokkal haladja meg a kritikus értéket.
A kiugró értékek detektálásra használhatjuk a Bonferroni-féle kiugró érték próbát, amely ha szignifikáns az adott pontban, akkor a studentizált reziduum elég nagy ahhoz, hogy kiugró értéket jósoljon. A próbát a car csomag outlierTest() függvényével hajthatjuk végre, amelynek egyetlen argumentuma most model=lm.1 modellobjektum.
library(car)
outlierTest(model = lm.1)##
## No Studentized residuals with Bonferonni p < 0.05
## Largest |rstudent|:
## rstudent unadjusted p-value Bonferonni p
## 78 2.190527 0.030882 NAA hatóerő (\(h_i\)) az \(X\) magyarázóváltozó értékinek átlagától mért távolságot méri, minél inkább közelítünk a regressziós egyenes végei felé, annál inkább nő a hatóerő mértéke. A nagyobb \(h_i\) hatóerővel rendelkező pontok, jobban képesek befolyásolni a regressziós egyenes alakját. A hatóerők \(1/n\) és \(1\) közé esnek, kiszámításuk: \(h_i=\frac{1}{n}+\frac{(x_i-\hat{x})^2}{\sum_{j=1}^n(x_j-\hat{x})^2}\) A hatóerőt a hatvalues() függvénnyel határozhatjuk meg az egyes pontokban.
print(hatvalues(lm.1), digits = 3)## 1 2 3 4 5 6 7 8 9 10
## 0.0339 0.0359 0.0320 0.0344 0.0330 0.0321 0.0343 0.0379 0.0334 0.0367
## 11 12 13 14 15 16 17 18 19 20
## 0.0261 0.0230 0.0238 0.0229 0.0246 0.0238 0.0246 0.0252 0.0275 0.0246
## 21 22 23 24 25 26 27 28 29 30
## 0.0162 0.0188 0.0176 0.0185 0.0186 0.0182 0.0170 0.0193 0.0165 0.0176
## 31 32 33 34 35 36 37 38 39 40
## 0.0128 0.0129 0.0135 0.0128 0.0119 0.0126 0.0125 0.0123 0.0119 0.0128
## 41 42 43 44 45 46 47 48 49 50
## 0.0101 0.0106 0.0102 0.0105 0.0101 0.0106 0.0105 0.0101 0.0104 0.0107
## 51 52 53 54 55 56 57 58 59 60
## 0.0102 0.0104 0.0105 0.0106 0.0102 0.0107 0.0102 0.0102 0.0101 0.0106
## 61 62 63 64 65 66 67 68 69 70
## 0.0130 0.0123 0.0134 0.0136 0.0119 0.0134 0.0119 0.0119 0.0122 0.0118
## 71 72 73 74 75 76 77 78 79 80
## 0.0178 0.0172 0.0165 0.0188 0.0174 0.0192 0.0178 0.0163 0.0165 0.0161
## 81 82 83 84 85 86 87 88 89 90
## 0.0250 0.0249 0.0239 0.0273 0.0269 0.0259 0.0232 0.0265 0.0241 0.0237
## 91 92 93 94 95 96 97 98 99 100
## 0.0342 0.0321 0.0361 0.0337 0.0323 0.0369 0.0364 0.0377 0.0325 0.0358plot(d$GDP, hatvalues(lm.1))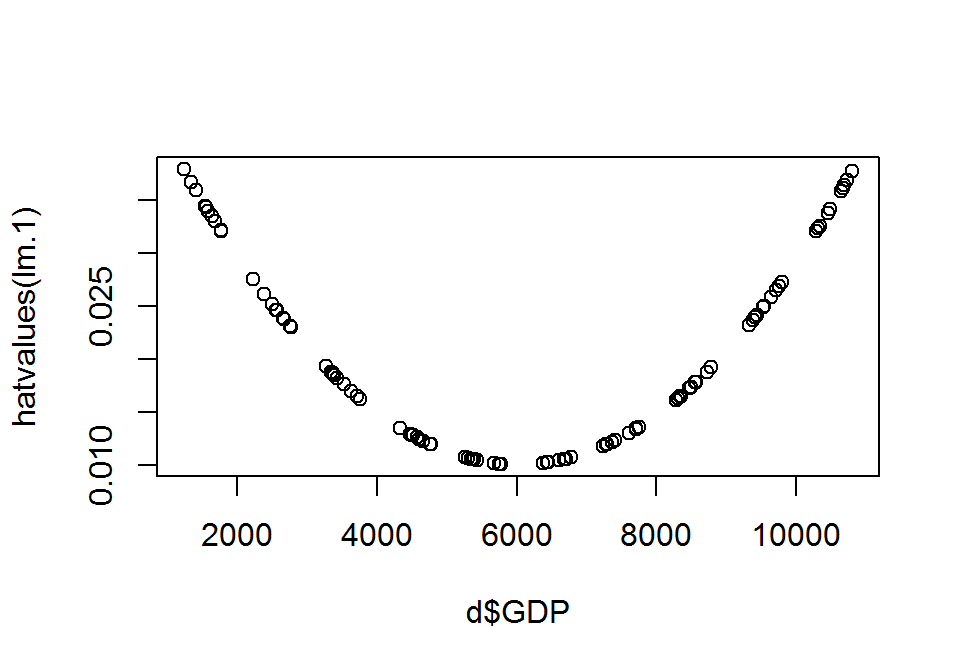
A torzító pontok a nagy hatóerővel rendelkező kiugró pontok. Ezek jelentősen befolyásolják a regressziós paraméterek értékét, így megtalálásuk különösen fontos.
Megvizsgálhatjuk, hogy az adott pont kihagyásával a regressziós paraméterek értékei mennyit változnának (DFBeta). Torzító pontra gyanakodhatunk, ha ez az érték nagyobb \(2/\sqrt{n}\)-nél. Ezeket a DFBeta különbségeket a dfbetas() függvénnyel írathatjuk ki, és a car csomag dfbatesPlots() függvényével ábrázolhatjuk.
print(dfbeta(lm.1), digits = 3)## (Intercept) GDP
## 1 -0.489481 0.000062103
## 2 0.950504 -0.000121724
## 3 0.082379 -0.000010348
## 4 -0.060849 0.000007738
## 5 0.039693 -0.000005011
## 6 -0.741468 0.000093180
## 7 0.771088 -0.000098008
## 8 -0.117741 0.000015203
## 9 -0.348035 0.000044044
## 10 -0.325145 0.000041777
## 11 0.658926 -0.000079533
## 12 -0.284133 0.000033274
## 13 0.204576 -0.000024166
## 14 -0.633692 0.000074130
## 15 0.022118 -0.000002632
## 16 0.371386 -0.000043829
## 17 -0.489020 0.000058196
## 18 0.366412 -0.000043847
## 19 -0.354434 0.000043249
## 20 -0.242944 0.000028928
## 21 -0.060226 0.000006236
## 22 -0.363941 0.000040029
## 23 0.088434 -0.000009492
## 24 -0.226503 0.000024789
## 25 0.361265 -0.000039629
## 26 -0.366536 0.000039864
## 27 -0.161412 0.000017062
## 28 0.297939 -0.000033084
## 29 0.049542 -0.000005168
## 30 0.559984 -0.000060117
## 31 -0.334549 0.000029294
## 32 0.077591 -0.000006856
## 33 -0.011001 0.000001010
## 34 -0.003468 0.000000303
## 35 0.264089 -0.000021044
## 36 -0.455659 0.000039012
## 37 -0.015567 0.000001318
## 38 -0.031090 0.000002578
## 39 -0.003354 0.000000267
## 40 0.270743 -0.000023566
## 41 -0.056254 0.000001479
## 42 0.359832 -0.000020807
## 43 -0.009774 0.000000338
## 44 0.000258 -0.000000014
## 45 -0.210134 0.000006056
## 46 -0.118208 0.000006561
## 47 0.167612 -0.000008935
## 48 -0.059209 0.000001526
## 49 0.068677 -0.000003452
## 50 -0.050425 0.000003028
## 51 0.087467 0.000005053
## 52 -0.011759 -0.000001440
## 53 -0.009879 -0.000001467
## 54 0.073460 0.000012128
## 55 -0.111800 -0.000008232
## 56 0.057195 0.000011672
## 57 -0.047343 -0.000003379
## 58 0.011830 0.000000859
## 59 0.144968 0.000008088
## 60 -0.033753 -0.000005622
## 61 -0.005996 0.000007286
## 62 -0.002179 0.000028393
## 63 0.044363 -0.000039877
## 64 0.002303 -0.000001847
## 65 -0.003469 -0.000006596
## 66 -0.017896 0.000015795
## 67 0.015896 0.000033896
## 68 -0.007419 -0.000013967
## 69 -0.000391 -0.000002579
## 70 0.003471 0.000004542
## 71 0.111742 -0.000040182
## 72 0.044035 -0.000016590
## 73 -0.109136 0.000044044
## 74 -0.012714 0.000004281
## 75 0.073781 -0.000027443
## 76 0.052843 -0.000017398
## 77 0.064033 -0.000023048
## 78 -0.159638 0.000065789
## 79 -0.015143 0.000006150
## 80 0.075575 -0.000031926
## 81 -0.003627 0.000000984
## 82 0.035053 -0.000009522
## 83 -0.185756 0.000051596
## 84 0.020506 -0.000005330
## 85 0.302837 -0.000079274
## 86 -0.076930 0.000020503
## 87 -0.011159 0.000003160
## 88 -0.251278 0.000066236
## 89 -0.082913 0.000022926
## 90 0.311250 -0.000086995
## 91 0.328386 -0.000078472
## 92 -0.032980 0.000008048
## 93 -0.475887 0.000111828
## 94 0.039165 -0.000009397
## 95 0.055835 -0.000013583
## 96 0.494095 -0.000115421
## 97 -0.104658 0.000024543
## 98 -0.167756 0.000038965
## 99 -0.005777 0.000001403
## 100 0.088657 -0.000020886library(car)
dfbetasPlots(lm.1)
Ha az összes együtthatóra egyidejűleg szeretnénk az egyes pontok torzító hatását vizsgálni, akkor a Cook-féle D-statisztikát (vagy Cook-féle távolságot) számolhatjuk ki: \(D_i=\frac{e_{i}^*}{r+1} \times \frac{h_i}{1-h_i}\). A \(D_i\) távolságértékek akkor nagyok, ha a kiugró értékről van szó (bal oldali szorzótnyzező a studentizált reziduummal), és ha nagy a hatóerő (jobb oldali szorzótényező). A Cook-féle távolság egy olyan standardizált index, amely azt méri, hogy a regressziós együtthatók együttvéve mennyit változnak, ha az adott pontot kihagyjuk a modellből. Nagyon gyanús az a pont, amelynél a \(D_i\) érték 1 felett van, de már \(4/n\) felettiek is gyanúsnak tekinthetők.
A Cook-féle távolságok a plot(lm.1, which=4) paranccsal írathatók ki, de részletesebb információt kapunk a standardizált reziduum-hatóerő ábra segítségével. Ehhez a which=5 argumentummal módosítsuk az előző rajzparancsot. A torzító pontok detektálását a 0,5-ös és 1-es Cook-féle D értékeknek megfelelő határok berajzolása segíti, illetve az ezen a határon kívül eső gyanús pontokat sorszámmal is ellátja.
print(cooks.distance(lm.1), digits = 4)## 1 2 3 4 5
## 0.01879255123 0.07055170079 0.00053515571 0.00029008567 0.00012389902
## 6 7 8 9 10
## 0.04334440807 0.04659446897 0.00107890087 0.00951338524 0.00824397380
## 11 12 13 14 15
## 0.03520316727 0.00672263363 0.00345695261 0.03347342885 0.00004013739
## 16 17 18 19 20
## 0.01140273557 0.01962207139 0.01096351860 0.01009932053 0.00484046036
## 21 22 23 24 25
## 0.00034775423 0.01179319366 0.00071684166 0.00459446477 0.01165645760
## 26 27 28 29 30
## 0.01212117264 0.00243376146 0.00781703219 0.00023312258 0.02873832631
## 31 32 33 34 35
## 0.01337900159 0.00071111084 0.00001359191 0.00000144469 0.00939434704
## 36 37 38 39 40
## 0.02555158421 0.00003023905 0.00012393277 0.00000151349 0.00883026810
## 41 42 43 44 45
## 0.00094446385 0.02445761612 0.00002540013 0.00000001335 0.01272898114
## 46 47 48 49 50
## 0.00273436920 0.00568361531 0.00105369669 0.00099895859 0.00046420802
## 51 52 53 54 55
## 0.00590197106 0.00018183519 0.00015400323 0.00948794007 0.01112770399
## 56 57 58 59 60
## 0.00727123652 0.00195618442 0.00012349469 0.01591591237 0.00202173212
## 61 62 63 64 65
## 0.00078389318 0.01471065081 0.02153363252 0.00004434735 0.00093114790
## 66 67 68 69 70
## 0.00335758030 0.02422944703 0.00418029903 0.00012902454 0.00046885811
## 71 72 73 74 75
## 0.01267037967 0.00225644101 0.01689367397 0.00013473695 0.00610159441
## 76 77 78 79 80
## 0.00217279721 0.00417210661 0.03835661795 0.00033108017 0.00921695624
## 81 82 83 84 85
## 0.00000554901 0.00052049361 0.01571397013 0.00015418962 0.03441716536
## 86 87 88 89 90
## 0.00235561407 0.00006038092 0.02424210675 0.00308499547 0.04502002766
## 91 92 93 94 95
## 0.02991987962 0.00032353194 0.05942214885 0.00043128828 0.00091787441
## 96 97 98 99 100
## 0.06280724196 0.00285441303 0.00710370320 0.00000975993 0.00207983860par(mfrow=c(1,2))
plot(x = lm.1, which = 4) # Cook-féle távolságok ábrája
plot(x = lm.1, which = 5) # standardizált reziduum-hatőerő ábra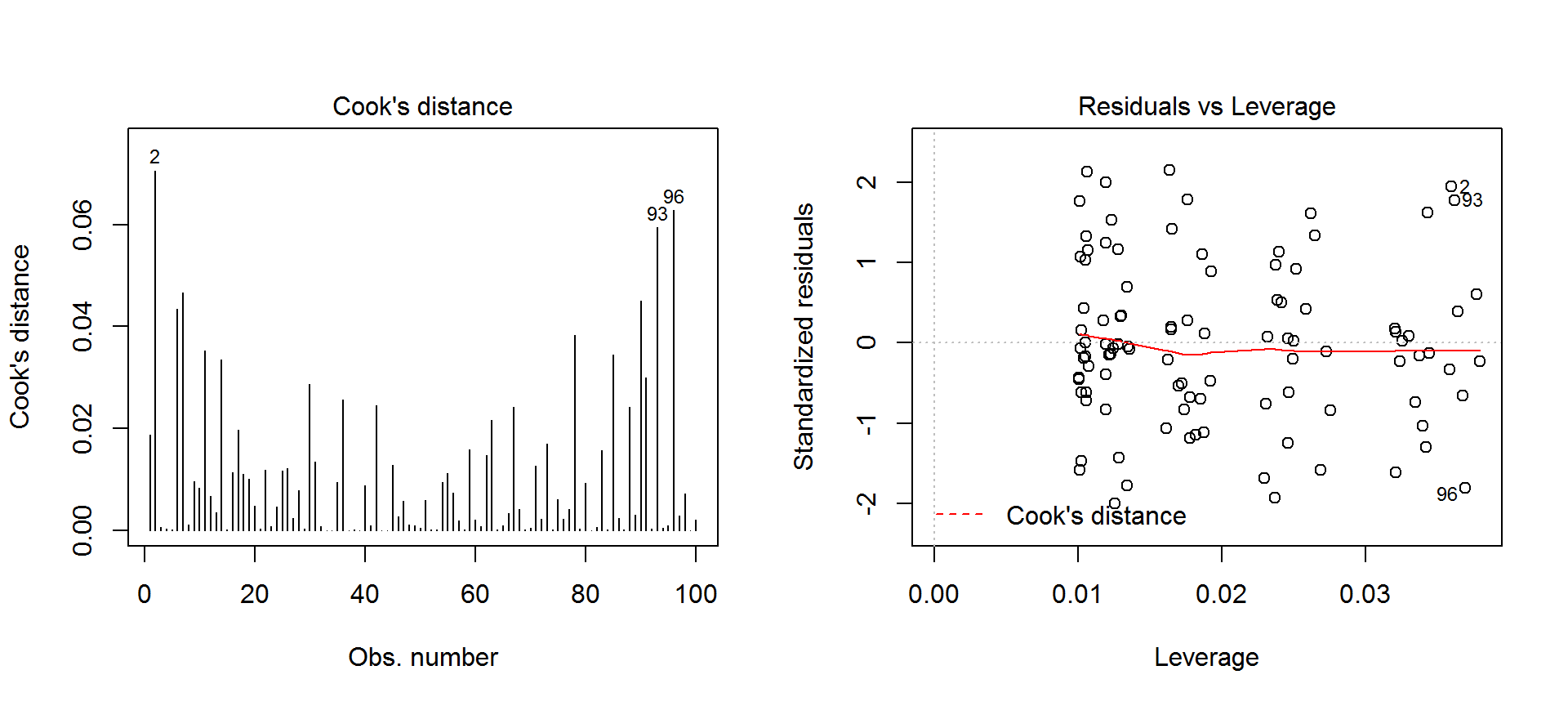
par(mfrow=c(1,1))A fenti ábráról leolvasható, hogy három mintaelem esetében (2., 93., és 96.) detektálható gyanús torzító pont. Ilyenkor érdemes a modell illesztését ezen pontok nélkül is elvégezni, és megnézni, hogy ténylegesen mennyit változnak a regressziós paraméterek.
lm.1##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d)
##
## Coefficients:
## (Intercept) GDP
## 22.480713 0.002586lm(ONGYILK ~ GDP, data = d, subset = -2)##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d, subset = -2)
##
## Coefficients:
## (Intercept) GDP
## 21.530209 0.002708lm(ONGYILK ~ GDP, data = d, subset = -93)##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d, subset = -93)
##
## Coefficients:
## (Intercept) GDP
## 22.956599 0.002474lm(ONGYILK ~ GDP, data = d, subset = -96)##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d, subset = -96)
##
## Coefficients:
## (Intercept) GDP
## 21.986617 0.002701lm(ONGYILK ~ GDP, data = d, subset = -c(2, 93, 96))##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d, subset = -c(2, 93, 96))
##
## Coefficients:
## (Intercept) GDP
## 21.492462 0.002716Látható, hogy a torzító pontoknak vélt mintaelemek eltávolítása után alig változott a regressziós együtthatók értéke.
Torzító pontok detektálására használhatjuk a DFITT mértéket is, amely a becsült érték változásának mértékét mutatja meg, amennyiben a kérdéses pontot kihagyjuk az elemzésből. A dfitts() függvénnyel számolhajuk ki az adott pontban az értékét. Ez a statisztika nagy mintaelemszám esetén standard normális eloszlást követ, így gyanús torzító pontnak a -3 és +3 intervallumon kívül eső adatpontokat nyílváníthatjuk.
print(dffits(lm.1), digits = 3)## 1 2 3 4 5 6 7
## -0.193938 0.381147 0.032554 -0.023966 0.015662 -0.296910 0.307854
## 8 9 10 11 12 13 14
## -0.046227 -0.137619 -0.128031 0.267589 -0.115698 0.082844 -0.261244
## 15 16 17 18 19 20 21
## 0.008914 0.150966 -0.198673 0.147963 -0.141913 -0.098080 -0.026243
## 22 23 24 25 26 27 28
## -0.153764 0.037686 -0.095607 0.152866 -0.155947 -0.069511 0.124905
## 29 30 31 32 33 34 35
## 0.021485 0.242516 -0.164479 0.037540 -0.005187 -0.001691 0.137466
## 36 37 38 39 40 41 42
## -0.229655 -0.007737 -0.015665 -0.001731 0.133145 -0.043280 0.225324
## 43 44 45 46 47 48 49
## -0.007091 0.000163 -0.160800 -0.073766 0.106656 -0.045720 0.044513
## 50 51 52 53 54 55 56
## -0.030327 0.108731 -0.018976 -0.017463 0.138308 -0.150080 0.120808
## 57 58 59 60 61 62 63
## -0.062350 0.015637 0.180384 -0.063386 0.039417 0.172740 -0.209888
## 64 65 66 67 68 69 70
## -0.009370 -0.042967 0.081733 0.223628 -0.091292 -0.015983 0.030478
## 71 72 73 74 75 76 77
## -0.159516 -0.066922 0.184779 0.016333 -0.110292 -0.065658 -0.091094
## 78 79 80 81 82 83 84
## 0.282288 0.025606 -0.135859 0.003314 -0.032106 0.177537 -0.017472
## 85 86 87 88 89 90 91
## -0.264408 0.068349 0.010933 0.221087 0.078247 -0.304351 -0.245498
## 92 93 94 95 96 97 98
## 0.025310 0.348658 -0.029223 -0.042638 -0.358658 0.075228 0.118805
## 99 100
## 0.004396 -0.064202plot(dffits(lm.1))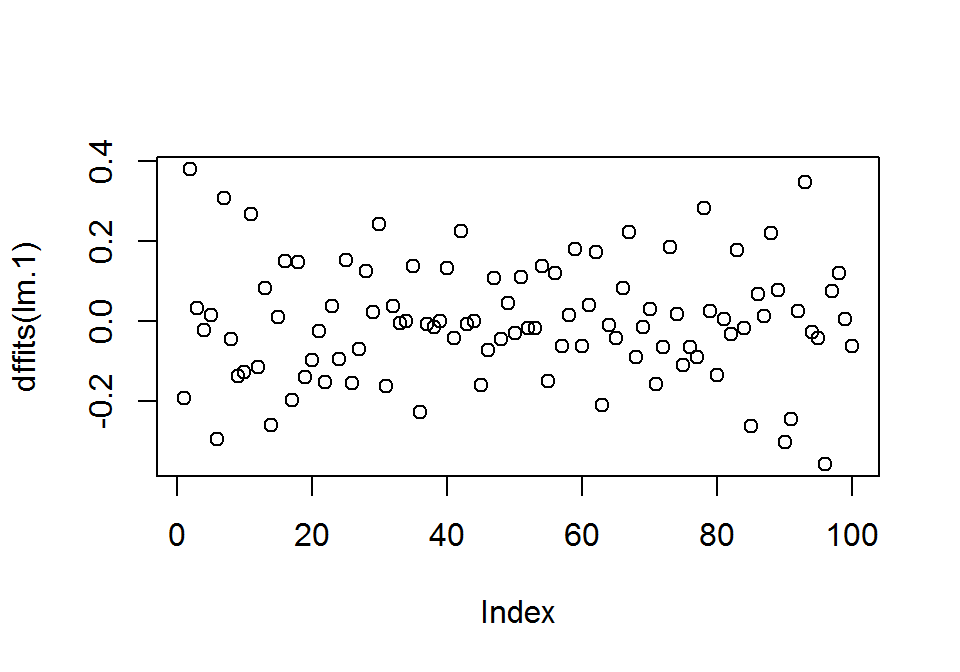
A torzító hatás vizsgálatára használhatjuk a COVRATIO mennyiséget. Kiszámítása: a vizsgált ponttal és anélkül kapott regressziós felület konfidencia-tartományai által határolt többdimenziós térfogatok hányadosának négyzete. A térfogat a pontosságot fejezi ki. Akkor gyanús a pont, ha \(\left| COVRATIO_i - 1\right| \geq 3p/n\). Ha értéke > 1, akkor a pont növeli a pontosságot, ha < 1, akkor csökkenti. A pontokhoz tartozó értékeit a covratio() függvénnyel határozhatjuk meg.
print(covratio(lm.1), digits = 3)## 1 2 3 4 5 6 7 8 9 10 11 12
## 1.034 0.979 1.054 1.057 1.055 0.999 1.001 1.060 1.044 1.050 0.993 1.033
## 13 14 15 16 17 18 19 20 21 22 23 24
## 1.040 0.985 1.046 1.026 1.013 1.029 1.034 1.038 1.037 1.014 1.037 1.030
## 25 26 27 28 29 30 31 32 33 34 35 36
## 1.014 1.012 1.032 1.024 1.037 0.972 0.991 1.032 1.035 1.034 1.001 0.951
## 37 38 39 40 41 42 43 44 45 46 47 48
## 1.034 1.033 1.033 1.005 1.027 0.938 1.031 1.032 0.979 1.021 1.009 1.027
## 49 50 51 52 53 54 55 56 57 58 59 60
## 1.027 1.030 1.007 1.031 1.031 0.995 0.986 1.004 1.023 1.031 0.967 1.024
## 61 62 63 64 65 66 67 68 69 70 71 72
## 1.032 0.984 0.969 1.035 1.030 1.024 0.950 1.018 1.033 1.031 1.010 1.033
## 73 74 75 76 77 78 79 80 81 82 83 84
## 0.996 1.040 1.024 1.036 1.029 0.942 1.037 1.014 1.047 1.046 1.019 1.049
## 85 86 87 88 89 90 91 92 93 94 95 96
## 0.996 1.044 1.045 1.011 1.041 0.968 1.021 1.054 0.992 1.056 1.054 0.990
## 97 98 99 100
## 1.056 1.053 1.055 1.056plot(covratio(lm.1))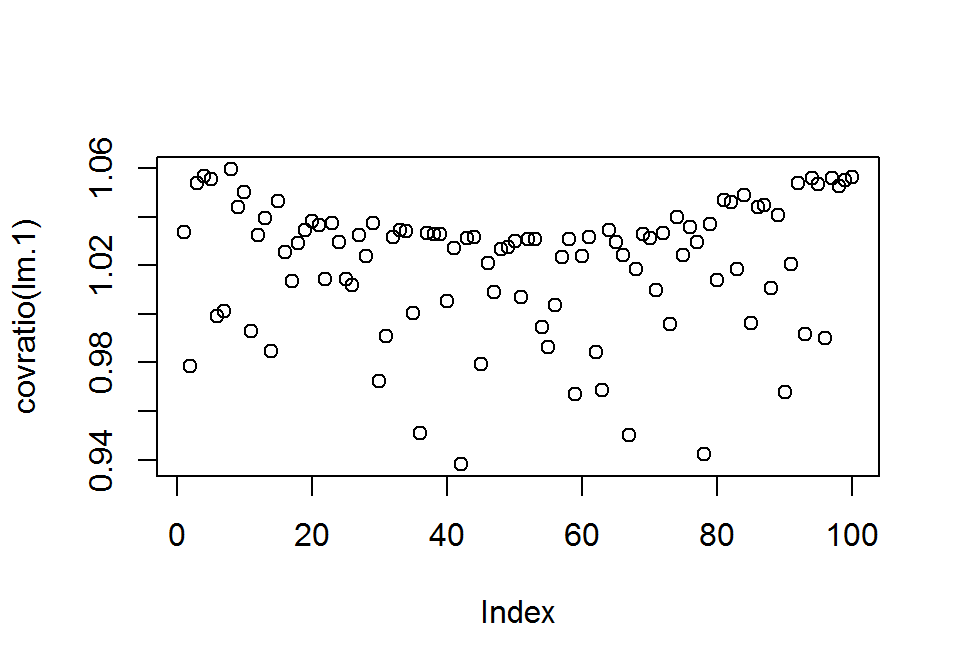
covratio(lm.1)[abs(covratio(lm.1)-1) >= 3*2/100] # a COVRATIO által gyanús torzító pontok## 42
## 0.9382327Látható, hogy a COVRATIO szerint a 42. adatpont gyanúsan nagy torzító erővel rendelkezik. Ha megvizsgáljuk a kihagyásával kapott regressziós együtthatókat, nem tapasztalunk nagy változást.
lm.1##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d)
##
## Coefficients:
## (Intercept) GDP
## 22.480713 0.002586lm(ONGYILK ~ GDP, data = d, subset = -42)##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d, subset = -42)
##
## Coefficients:
## (Intercept) GDP
## 22.120880 0.002607Az influence.measures() függvénnyel több mérték alapján ellenőrizhetjük, hogy melyik pont gyanús torzító hatás szempontjából. Ezeket a pontokat az inf oszlopban * jelöli. A listázott mértékek: DFBeta, DFFIT, COVRATIO, Cook-féle távolság és hatóerő.
influence.measures(lm.1)## Influence measures of
## lm(formula = ONGYILK ~ GDP, data = d) :
##
## dfb.1_ dfb.GDP dffit cov.r cook.d hat inf
## 1 -0.192307 0.1628852 -0.193938 1.034 0.0187925512 0.0339
## 2 0.378775 -0.3238242 0.381147 0.979 0.0705517008 0.0359
## 3 0.032193 -0.0269979 0.032554 1.054 0.0005351557 0.0320
## 4 -0.023778 0.0201864 -0.023966 1.057 0.0002900857 0.0344
## 5 0.015510 -0.0130727 0.015662 1.055 0.0001238990 0.0330
## 6 -0.293656 0.2463640 -0.296910 0.999 0.0433444081 0.0321
## 7 0.305401 -0.2591401 0.307854 1.001 0.0465944690 0.0343
## 8 -0.046018 0.0396682 -0.046227 1.060 0.0010789009 0.0379
## 9 -0.136371 0.1152108 -0.137619 1.044 0.0095133852 0.0334
## 10 -0.127325 0.1092146 -0.128031 1.050 0.0082439738 0.0367
## 11 0.260977 -0.2102895 0.267589 0.993 0.0352031673 0.0261
## 12 -0.111344 0.0870472 -0.115698 1.033 0.0067226336 0.0230
## 13 0.080050 -0.0631265 0.082844 1.040 0.0034569526 0.0238
## 14 -0.251284 0.1962386 -0.261244 0.985 0.0334734288 0.0229
## 15 0.008642 -0.0068666 0.008914 1.046 0.0000401374 0.0246
## 16 0.145810 -0.1148768 0.150966 1.026 0.0114027356 0.0238
## 17 -0.192611 0.1530234 -0.198673 1.013 0.0196220714 0.0246
## 18 0.143792 -0.1148728 0.147963 1.029 0.0109635186 0.0252
## 19 -0.138995 0.1132262 -0.141913 1.034 0.0100993205 0.0275
## 20 -0.095111 0.0756063 -0.098080 1.038 0.0048404604 0.0246
## 21 -0.023537 0.0162710 -0.026243 1.037 0.0003477542 0.0162
## 22 -0.143106 0.1050763 -0.153764 1.014 0.0117931937 0.0188
## 23 0.034568 -0.0247709 0.037686 1.037 0.0007168417 0.0176
## 24 -0.088722 0.0648226 -0.095607 1.030 0.0045944648 0.0185
## 25 0.142050 -0.1040244 0.152866 1.014 0.0116564576 0.0186
## 26 -0.144182 0.1046843 -0.155947 1.012 0.0121211726 0.0182
## 27 -0.063159 0.0445699 -0.069511 1.032 0.0024337615 0.0170
## 28 0.116889 -0.0866506 0.124905 1.024 0.0078170322 0.0193
## 29 0.019360 -0.0134820 0.021485 1.037 0.0002331226 0.0165
## 30 0.222472 -0.1594425 0.242516 0.972 0.0287383263 0.0176
## 31 -0.132114 0.0772272 -0.164479 0.991 0.0133790016 0.0128
## 32 0.030334 -0.0178947 0.037540 1.032 0.0007111108 0.0129
## 33 -0.004298 0.0026348 -0.005187 1.035 0.0000135919 0.0135
## 34 -0.001355 0.0007891 -0.001691 1.034 0.0000014447 0.0128
## 35 0.104016 -0.0553328 0.137466 1.001 0.0093943470 0.0119
## 36 -0.181801 0.1039113 -0.229655 0.951 0.0255515842 0.0126
## 37 -0.006083 0.0034392 -0.007737 1.034 0.0000302390 0.0125
## 38 -0.012149 0.0067244 -0.015665 1.033 0.0001239328 0.0123
## 39 -0.001310 0.0006977 -0.001731 1.033 0.0000015135 0.0119
## 40 0.106533 -0.0619051 0.133145 1.005 0.0088302681 0.0128
## 41 -0.022001 0.0038604 -0.043280 1.027 0.0009444639 0.0101
## 42 0.143975 -0.0555772 0.225324 0.938 0.0244576161 0.0106 *
## 43 -0.003819 0.0008828 -0.007091 1.031 0.0000254001 0.0102
## 44 0.000101 -0.0000365 0.000163 1.032 0.0000000134 0.0105
## 45 -0.083171 0.0160026 -0.160800 0.979 0.0127289811 0.0101
## 46 -0.046308 0.0171588 -0.073766 1.021 0.0027343692 0.0106
## 47 0.065852 -0.0234343 0.106656 1.009 0.0056836153 0.0105
## 48 -0.023159 0.0039835 -0.045720 1.027 0.0010536967 0.0101
## 49 0.026860 -0.0090119 0.044513 1.027 0.0009989586 0.0104
## 50 -0.019711 0.0079016 -0.030327 1.030 0.0004642080 0.0107
## 51 0.034378 0.0132575 0.108731 1.007 0.0059019711 0.0102
## 52 -0.004595 -0.0037575 -0.018976 1.031 0.0001818352 0.0104
## 53 -0.003861 -0.0038282 -0.017463 1.031 0.0001540032 0.0105
## 54 0.028967 0.0319263 0.138308 0.995 0.0094879401 0.0106
## 55 -0.044172 -0.0217128 -0.150080 0.986 0.0111277040 0.0102
## 56 0.022503 0.0306567 0.120808 1.004 0.0072712365 0.0107
## 57 -0.018534 -0.0088307 -0.062350 1.023 0.0019561844 0.0102
## 58 0.004623 0.0022412 0.015637 1.031 0.0001234947 0.0102
## 59 0.057563 0.0214402 0.180384 0.967 0.0159159124 0.0101
## 60 -0.013214 -0.0146926 -0.063386 1.024 0.0020217321 0.0106
## 61 -0.002344 0.0190163 0.039417 1.032 0.0007838932 0.0130
## 62 -0.000862 0.0749684 0.172740 0.984 0.0147106508 0.0123
## 63 0.017621 -0.1057408 -0.209888 0.969 0.0215336325 0.0134
## 64 0.000900 -0.0048185 -0.009370 1.035 0.0000443474 0.0136
## 65 -0.001357 -0.0172199 -0.042967 1.030 0.0009311479 0.0119
## 66 -0.007010 0.0413051 0.081733 1.024 0.0033575803 0.0134
## 67 0.006342 0.0902812 0.223628 0.950 0.0242294470 0.0119
## 68 -0.002909 -0.0365624 -0.091292 1.018 0.0041802990 0.0119
## 69 -0.000153 -0.0067267 -0.015983 1.033 0.0001290245 0.0122
## 70 0.001357 0.0118518 0.030478 1.031 0.0004688581 0.0118
## 71 0.043976 -0.1055698 -0.159516 1.010 0.0126703797 0.0178
## 72 0.017228 -0.0433325 -0.066922 1.033 0.0022564410 0.0172
## 73 -0.043087 0.1160846 0.184779 0.996 0.0168936740 0.0165
## 74 -0.004968 0.0111689 0.016333 1.040 0.0001347369 0.0188
## 75 0.028931 -0.0718375 -0.110292 1.024 0.0061015944 0.0174
## 76 0.020671 -0.0454332 -0.065658 1.036 0.0021727972 0.0192
## 77 0.025079 -0.0602603 -0.091094 1.029 0.0041721066 0.0178
## 78 -0.063900 0.1758000 0.282288 0.942 0.0383566179 0.0163
## 79 -0.005918 0.0160444 0.025606 1.037 0.0003310802 0.0165
## 80 0.029700 -0.0837607 -0.135859 1.014 0.0092169562 0.0161
## 81 -0.001417 0.0025666 0.003314 1.047 0.0000055490 0.0250
## 82 0.013699 -0.0248424 -0.032106 1.046 0.0005204936 0.0249
## 83 -0.073060 0.1354735 0.177537 1.019 0.0157139701 0.0239
## 84 0.008013 -0.0139044 -0.017472 1.049 0.0001541896 0.0273
## 85 0.119863 -0.2094672 -0.264408 0.996 0.0344171654 0.0269
## 86 -0.030086 0.0535285 0.068349 1.044 0.0023556141 0.0259
## 87 -0.004360 0.0082437 0.010933 1.045 0.0000603809 0.0232
## 88 -0.099088 0.1743680 0.221087 1.011 0.0242421067 0.0265
## 89 -0.032438 0.0598767 0.078247 1.041 0.0030849955 0.0241
## 90 0.123985 -0.2313460 -0.304351 0.968 0.0450200277 0.0237
## 91 0.129432 -0.2064812 -0.245498 1.021 0.0299198796 0.0342
## 92 -0.012888 0.0209942 0.025310 1.054 0.0003235319 0.0321
## 93 -0.189024 0.2965321 0.348658 0.992 0.0594221488 0.0361
## 94 0.015305 -0.0245136 -0.029223 1.056 0.0004312883 0.0337
## 95 0.021823 -0.0354400 -0.042638 1.054 0.0009178744 0.0323
## 96 0.196370 -0.3062371 -0.358658 0.990 0.0628072420 0.0369
## 97 -0.040925 0.0640686 0.075228 1.056 0.0028544130 0.0364
## 98 -0.065669 0.1018265 0.118805 1.053 0.0071037032 0.0377
## 99 -0.002257 0.0036585 0.004396 1.055 0.0000097599 0.0325
## 100 0.034661 -0.0545119 -0.064202 1.056 0.0020798386 0.0358A fenti outputból kiolvasható, hogy egyedül a 42. pont tekitnhető gyanúsnak, a korábban már vizsgált túl alacsony COVRATIO értéke miatt.
Érdemes megemlíteni a car csomag influenceIndexPlot() függvényét, amellyel több mérték alapján grafikus ellenőrzést végezhetünk. Ezek rendre, fentről lefelé: Cook-távolság, standardizált reziduumok, Bonferroni kiugró érték próba p értékei és végül, a hatóerők.
library(car)
influenceIndexPlot(lm.1)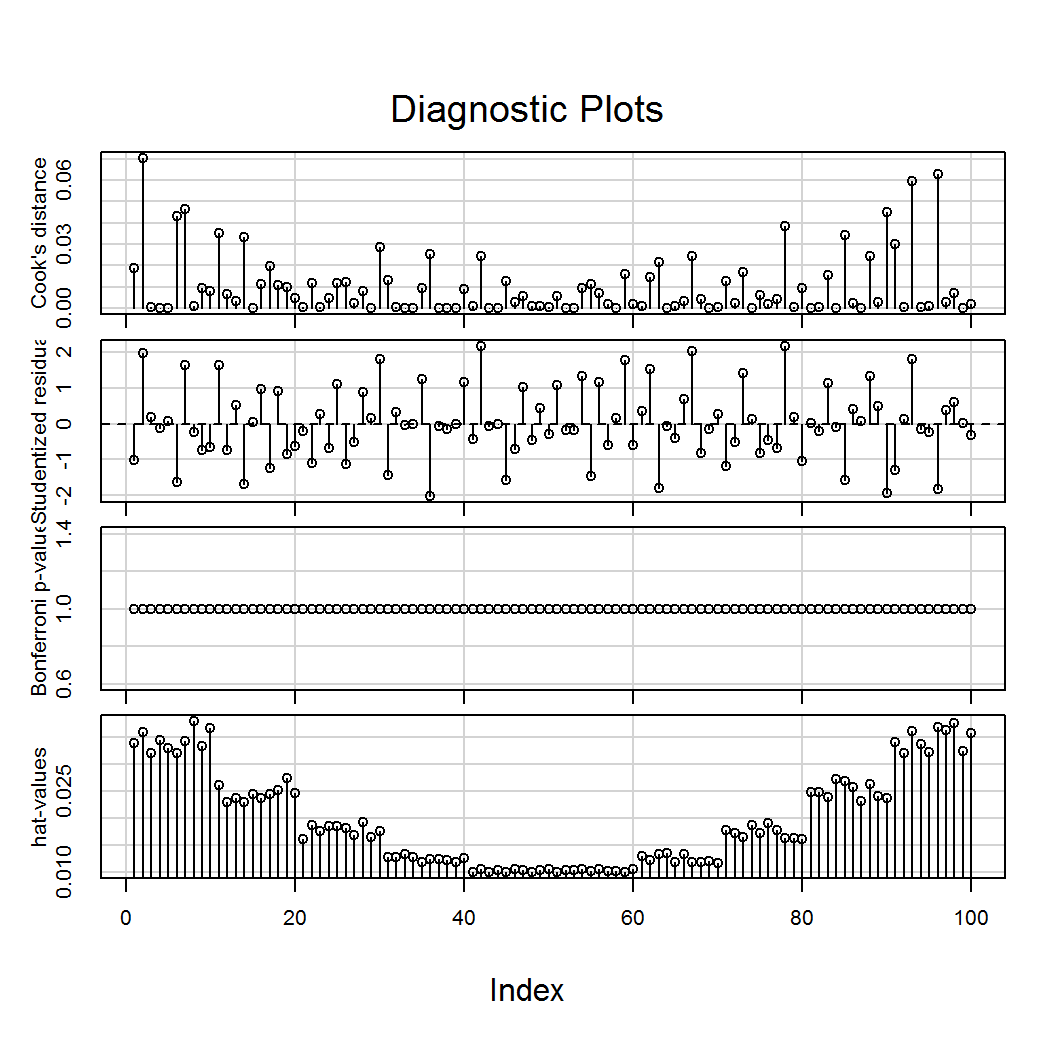
Alkalmazási feltételek ellenőrzése (1): a reziduálisok normalitása.
A reziduumok normalitásának ellenőrzése nem tér el a változók normális eloszlásának szokásos vizsgálatától. Történhet hisztogram és QQ-ábra segítségével, valamint használhatjuk a Shapiro–Wilk-próbát is.
par(mfrow=c(1,2))
hist(residuals(lm.1))
plot(lm.1, which = 2)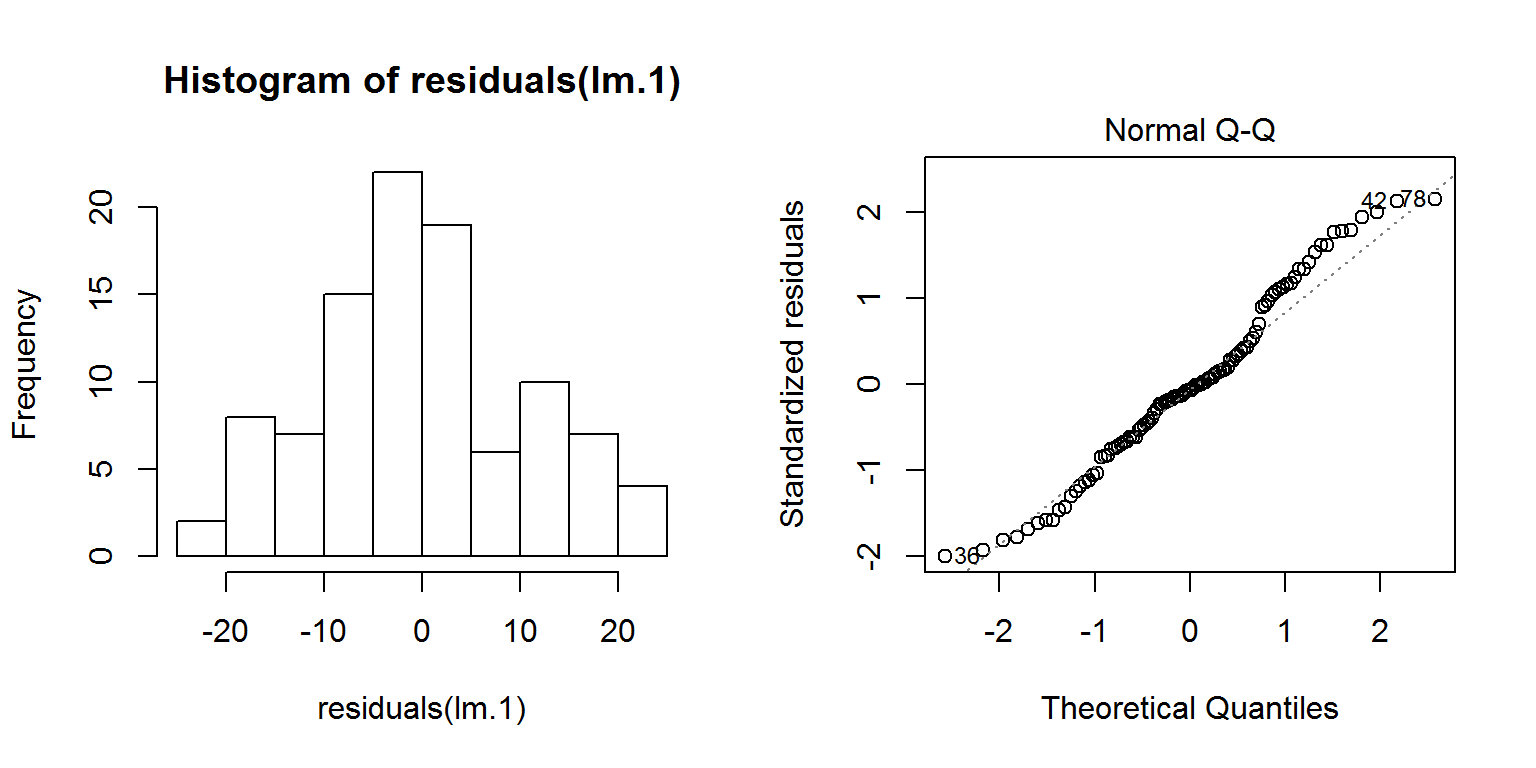
par(mfrow=c(1,1))
shapiro.test(residuals(lm.1))##
## Shapiro-Wilk normality test
##
## data: residuals(lm.1)
## W = 0.97831, p-value = 0.09815Látható, hogy a reziduumok normális eloszlását mindhárom fenti eljárás támogatja.
Alkalmazási feltételek ellenőrzése (2): a reziduálisok varianciája állandó.
A hibatag szórásának állandósága azt jelenti, hogy \(X\) értékeinek változásával a reziduumok nagyságrendje nem változik. A szórás-becsült érték ábra (scale-location plot) a becsült értékek (\(\hat{y}_i\)) függvényében mutatja meg a standardizált reziduumok abszolút értékének négyzetgyökét (\(\sqrt{\left|\varepsilon_i\right|}\)). A szórás-becsült érték ábra megrajzolásához a plot() függvényt használjuk, melynek argumentumai a modellobjektum és a which=3.
plot(x = lm.1, which = 3)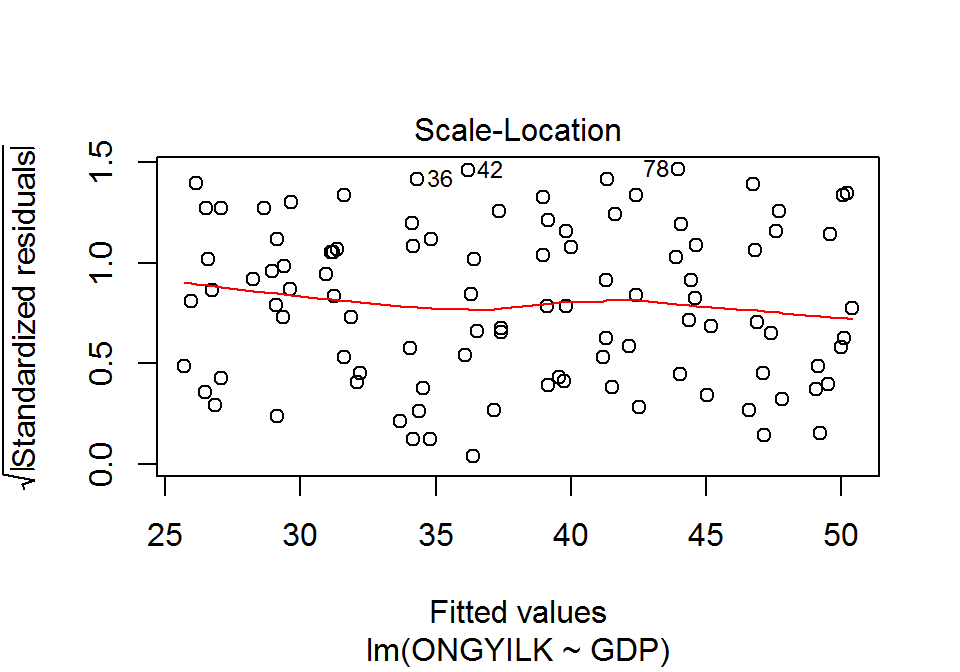
Állandó szórás esetén a piros simított görbének nagyjából vízszintesnek kellene lennie. Mivel nem látunk tendenciát az ábrán, ezért feltételezhetjük a reziduumok szórásának állandóságát.
Statisztikai próbával is tesztelhetjük a szórás állandóságát. A Breusch–Pagan-próba vagy nem-konstans variancia próba (non-constant variance test) azt teszteli, hogy a reziduumok varianciája független-e a függő változó értékeitől. A nullhipotézis szerint független, vagyis ekkor a szórások állandósága megvalósul, az ellenhipotézis szerint nem, vagyis ekkor heteroszkedaszticitás valósul meg. A próba végrehatását a car csomag ncvTest() függvényével kezdeményezhetjük. Az egyetlen argumentum a modellobjektum.
library(car)
ncvTest(lm.1)## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 0.02570756 Df = 1 p = 0.8726166Látható, hogy a szórások állandóságát a Breusch–Pagan-próba is támogatja (\(\chi^2(1)=0,0257; p=0,8726\)).
Alkalmazási feltételek ellenőrzése (3): a lineáris kapcsolat. A magyarázó változó és a függő változó közötti kapcsolatot több módszerrel ellenőrizhetjük. Egyszerű lineáris regresszió esetén a két változó szórásdiagramja már kielégítő tájékozódást nyújt. Ezt korábban láttuk, most megismételjük.
library(car)
scatterplot(x = d$GDP, y = d$ONGYILK, spread = F)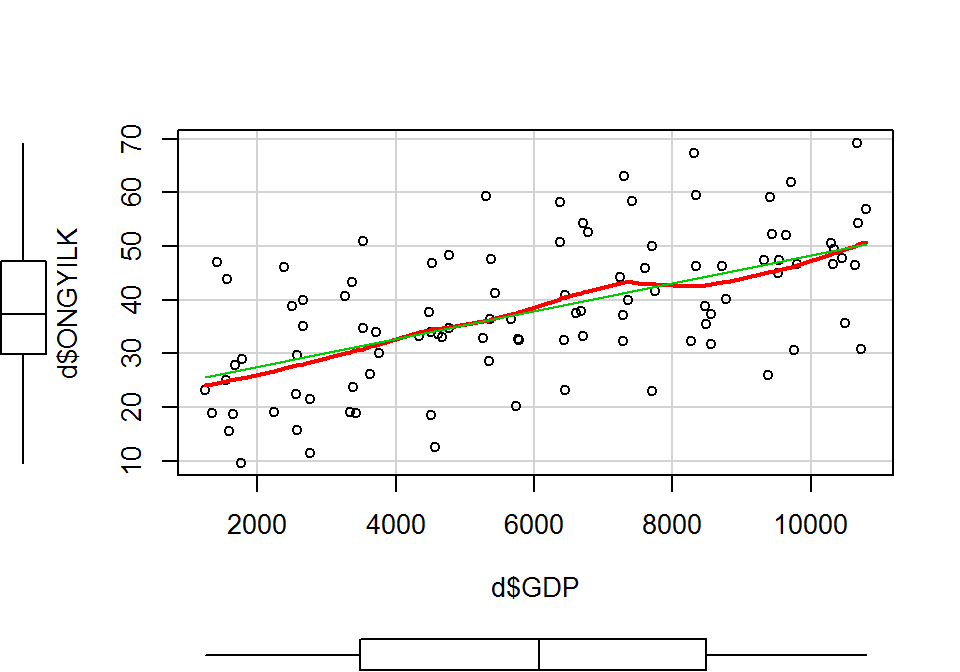
Az \(\hat{y}_i\) és \(y_i\) kapcsolatát bemutató szórásdiagram más esetekben is használható.
plot(x = fitted(lm.1), d$ONGYILK)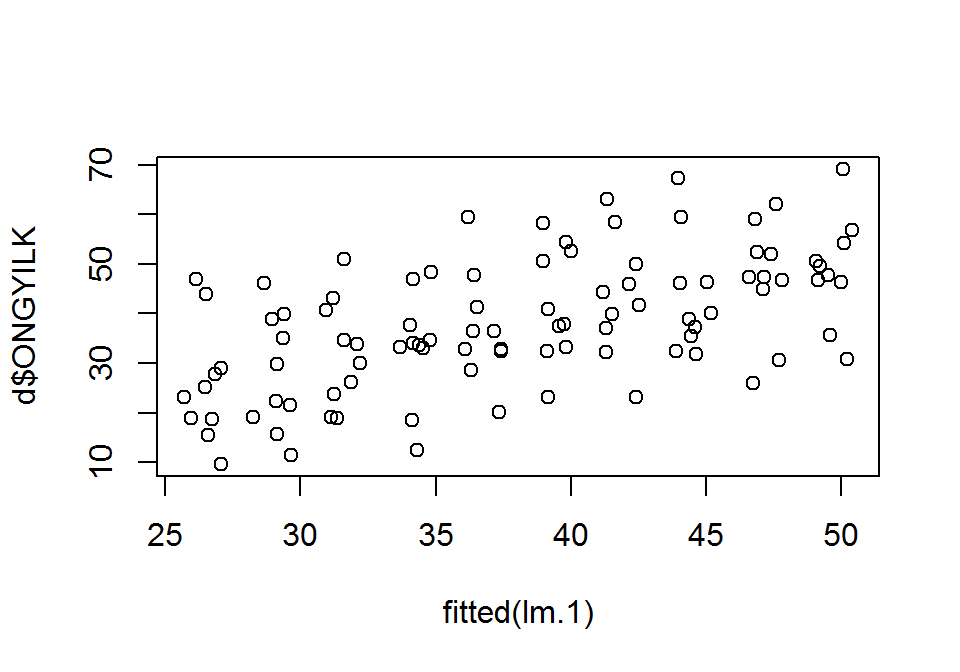
Az ábráról leolvasható lineáris kapcsolat a modell linearitását támogatja.
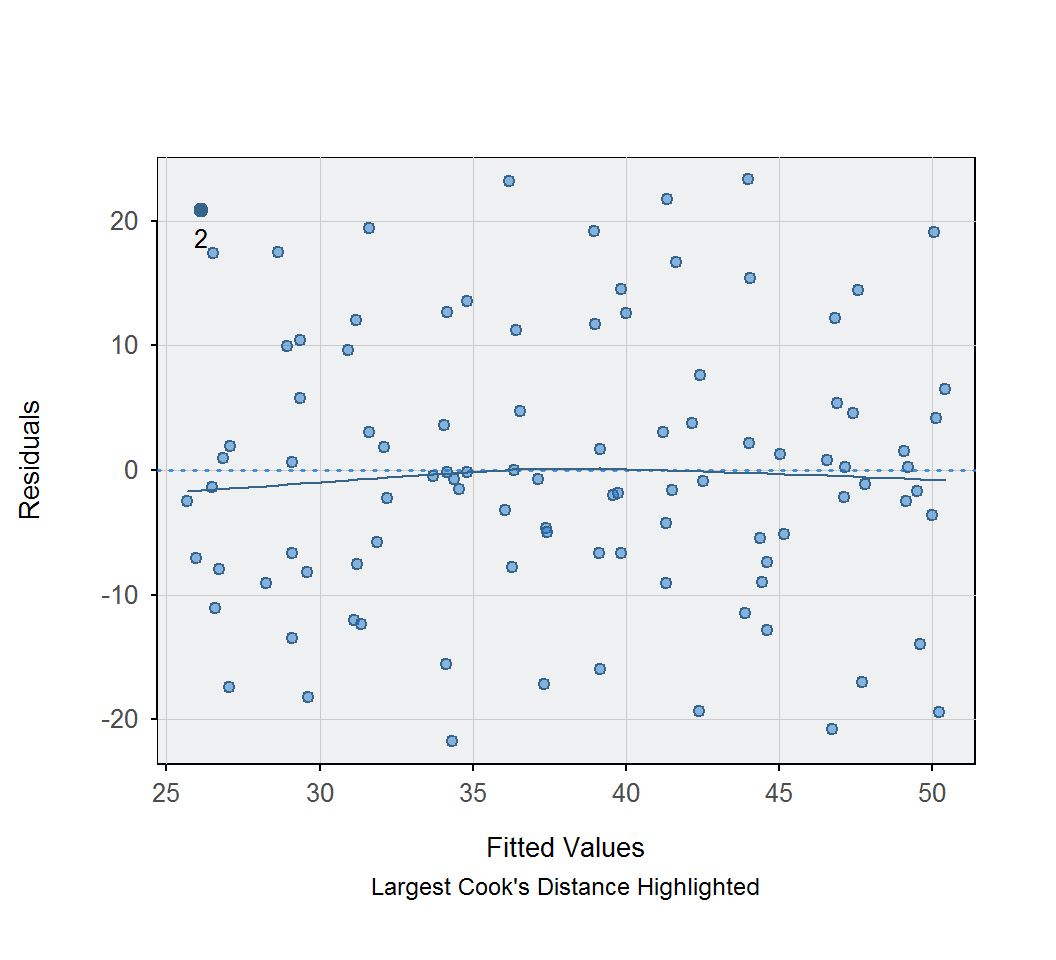
Részletesebb információt ad a becsült értékek és a standardizált reziduumok közötti kapcsolatot feltáró ábra. A reziduum-becsült érték ábra megrajzolásához a plot() függvényt használjuk, melynek argumentumai a modellobjektum és a which=1.
plot(x = lm.1, which = 1)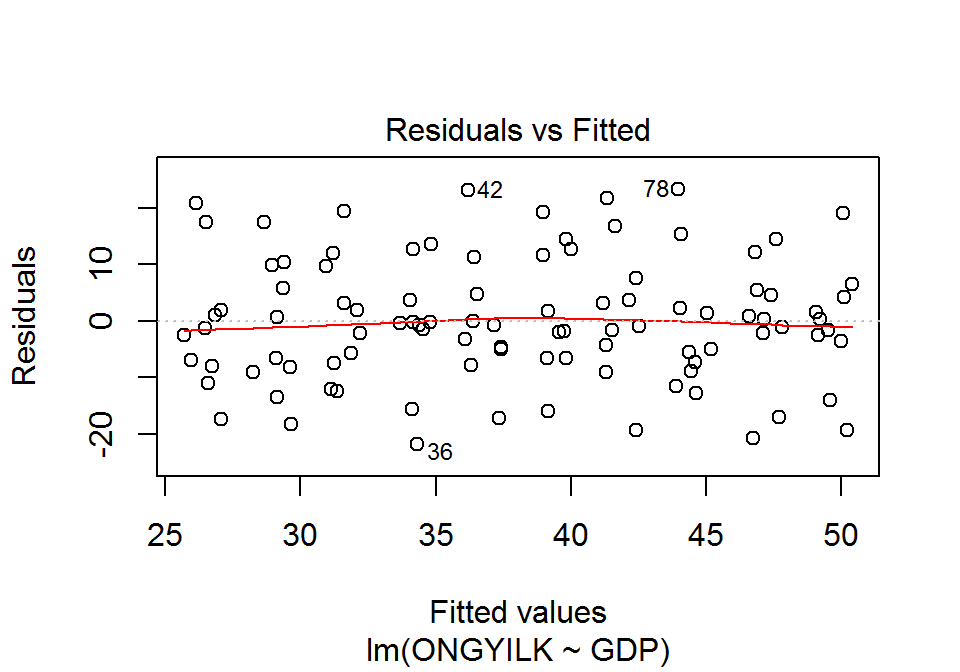
Az ábrán megjelenő piros vonal ideális esetben (tökéletes lineáris kapcsolat esetén) vízszintes, de ettől kisebb eltérések még nem sértik a linearitást.
Még részletesebb vizsgálatra van lehetőségünk a car csomag residualPlots() függvényével. Egyrészt a reziduum-becsült érték ábra mellet, minden magyarázó változóra megkapjuk az ábrát, másrészt hipotézisvizsgálatok eredményét látjuk a magyarázó változóra (GDP sor) és a becsült értékekre (Tukey test sor) vonatkozóan. A hipotézisvizsgálatok a vizsgált változó (GDP és \(\hat{Y}\)) négyzetét helyezik a modellbe, és annak együtthatójára vonatkozó t-próbastatisztika értékkel, illetve annak szignifikanciájára vonatkozó p-értékkel tér vissza. Amennyiben szignifikáns hatás mutatható ki, akkor van valamilyen nem-lineáris összetevője a változónak és a reziduumoknak.
library(car)
residualPlots(lm.1)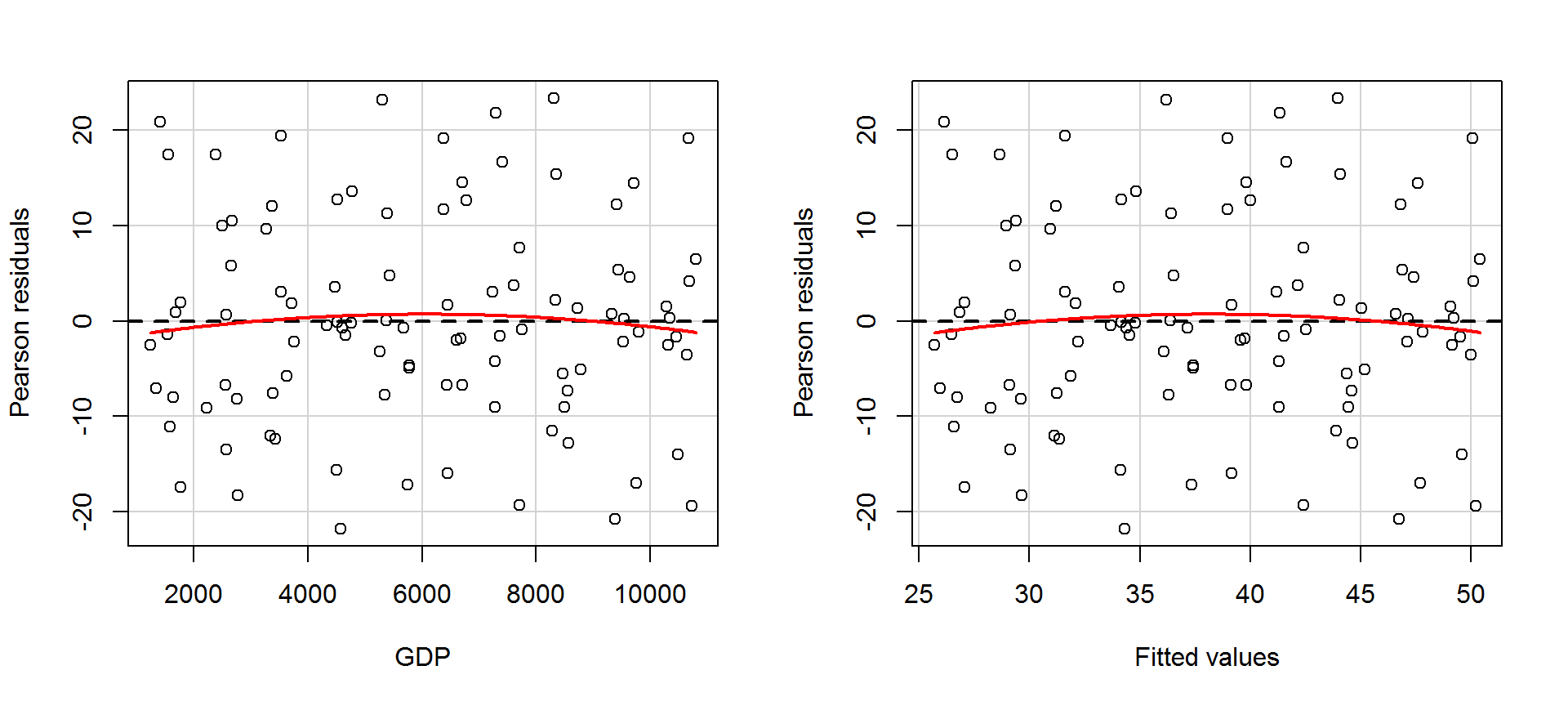
## Test stat Pr(>|t|)
## GDP -0.563 0.574
## Tukey test -0.563 0.573A fenti eredményekből leolvasható, hogy a modell linearitására vonatkozó feltétel nem serül.
A regressziós diagnosztika zárásaként két függvényt mutatunk be, amely összefoglalja, de nem helyettesíti a fentieket. A gvlma csomag gvlma() függvényével számos alkalmazási feltétel ellenőrzésére hipotézisvizsgálat eszközeivel nyílik módunk. A plot() függvénnyel pedig a sok szóba jöhető diagnosztikus ábrából tudunk hatot megjeleníteni.
library(gvlma)
gvmodel <- gvlma(lm.1)
summary(gvmodel)##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.7691 -7.1339 -0.7589 5.9267 23.3114
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.4807127 2.5462232 8.829 4.19e-14
## GDP 0.0025860 0.0003814 6.780 9.09e-10
##
## Residual standard error: 10.94 on 98 degrees of freedom
## Multiple R-squared: 0.3193, Adjusted R-squared: 0.3124
## F-statistic: 45.97 on 1 and 98 DF, p-value: 0.0000000009095
##
##
## ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
## USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
## Level of Significance = 0.05
##
## Call:
## gvlma(x = lm.1)
##
## Value p-value Decision
## Global Stat 2.01725 0.7326 Assumptions acceptable.
## Skewness 0.63508 0.4255 Assumptions acceptable.
## Kurtosis 1.02936 0.3103 Assumptions acceptable.
## Link Function 0.32620 0.5679 Assumptions acceptable.
## Heteroscedasticity 0.02661 0.8704 Assumptions acceptable.par(mfrow=c(2,3))
plot(lm.1, which = 1)
plot(lm.1, which = 2)
plot(lm.1, which = 3)
plot(lm.1, which = 4)
plot(lm.1, which = 5)
plot(lm.1, which = 6)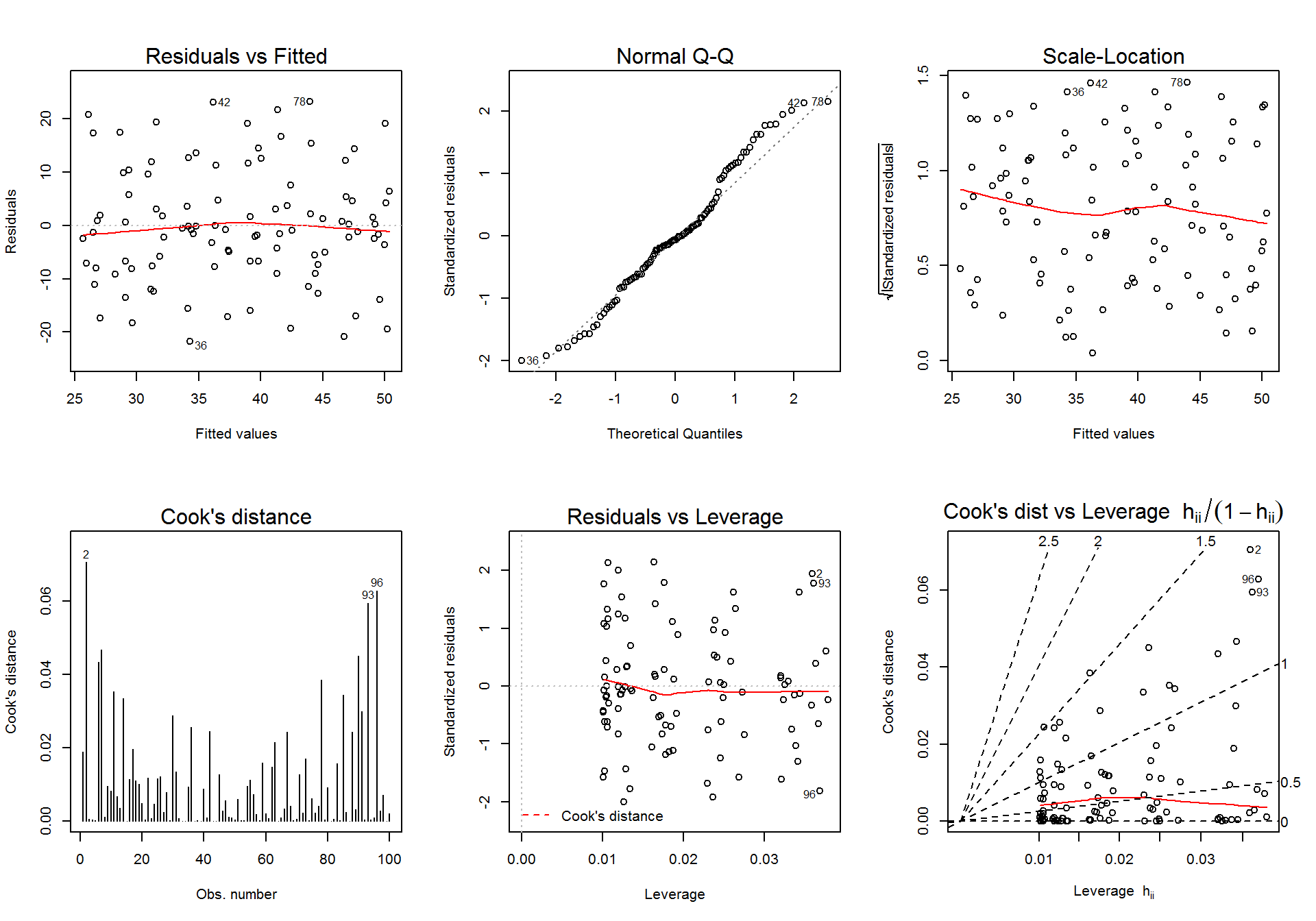
par(mfrow=c(1,1))Hipotézisvizsgálatok az együtthatókra és a teljes modellre.
summary(lm.1) # hipotézisvizsgálatok az együtthatókra és a teljes modellre##
## Call:
## lm(formula = ONGYILK ~ GDP, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.7691 -7.1339 -0.7589 5.9267 23.3114
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.4807127 2.5462232 8.829 4.19e-14
## GDP 0.0025860 0.0003814 6.780 9.09e-10
##
## Residual standard error: 10.94 on 98 degrees of freedom
## Multiple R-squared: 0.3193, Adjusted R-squared: 0.3124
## F-statistic: 45.97 on 1 and 98 DF, p-value: 0.0000000009095anova(lm.1) # hipotézisvizsgálat a teljes modellre## Analysis of Variance Table
##
## Response: ONGYILK
## Df Sum Sq Mean Sq F value Pr(>F)
## GDP 1 5497.9 5497.9 45.972 0.0000000009095
## Residuals 98 11720.2 119.6lm.0 <- lm(ONGYILK ~ 1, data = d) # a nullmodell
summary(lm.0) ##
## Call:
## lm(formula = ONGYILK ~ 1, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -28.4174 -8.1511 -0.6713 9.0277 31.1024
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 38.071 1.319 28.87 <2e-16
##
## Residual standard error: 13.19 on 99 degrees of freedomanova(lm.0, lm.1) # összehasonlítás a nullmodellel ## Analysis of Variance Table
##
## Model 1: ONGYILK ~ 1
## Model 2: ONGYILK ~ GDP
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 99 17218
## 2 98 11720 1 5497.9 45.972 0.0000000009095Az egyszerű lineáris regresszió kézi számítása.
atlag.x <- mean(d$GDP, na.rm = T)
atlag.y <- mean(d$ONGYILK, na.rm = T)
n <- length(d$GDP)
b.1 <- sum((d$GDP-atlag.x)*(d$ONGYILK-atlag.y))/sum((d$GDP-atlag.x)^2)
b.1## [1] 0.002586034b.0 <- atlag.y - b.1*atlag.x
b.0## [1] 22.48071SST <- sum((d$ONGYILK-atlag.y)^2)
SSR <- sum((fitted(lm.1)-atlag.y)^2)
SSH <- sum((fitted(lm.1)-d$ONGYILK)^2)
SSR## [1] 5497.938SSH## [1] 11720.2F.stat <- SSR / (SSH / (n - 2))
F.stat## [1] 45.97172pf(q = F.stat, df1 = 1, df2 = n - 2, lower.tail = F)## [1] 0.0000000009094709Alternatívák az egyszerű lineáris regresszióra.
A userfriendlyscience csomag regr() függvénye részletes outputot szolgáltat a lineáris regresszióról, valamint ábra megjelenítésére is lehetségünk van (plot=T). Az outputban a nem standardizált együtthatók mellett a standardizáltak is megjelennek, illetve a 95%-os konfidenciaintervallumokat is láthatjuk (conf.level=0.95). Az outputban megjelenő számértékek és külön a \(p\) értékek pontosságát a digits= és pvalueDigits= argumentumokkal szabályozhatjuk.
library(userfriendlyscience)
regr(ONGYILK ~ GDP, dat = d, conf.level = 0.95, digits = 7, pvalueDigits = 7, plot = T)## Regression analysis for formula: ONGYILK ~ GDP
##
## Significance test of the entire model (all predictors together):
## Multiple R-squared: [0.1740531, 0.4645684] (point estimate = 0.3193108, adjusted = 0.312365)
## Test for significance: F[1, 98] = 45.9717195, p < .0000001
##
## Raw regression coefficients (unstandardized beta values, called 'B' in SPSS):
##
## 95% conf. int. estimate se t
## (Intercept) [17.4278156; 27.5336098] 22.480713 2.5462232 8.829042
## GDP [0.0018291; 0.0033429] 0.002586 0.0003814 6.780245
## p
## (Intercept) < .0000001
## GDP < .0000001
##
## Scaled regression coefficients (standardized beta values, called 'Beta' in SPSS):
##
## 95% conf. int. estimate se t p
## (Intercept) [-0.1645595; 0.1645595] 0.0000000 0.0829238 0.000000 1
## GDP [0.3996874; 0.7304644] 0.5650759 0.0833415 6.780245 <.0000001
A lessR csomag Regression() függvényével a szokásos regressziós hipotézisvizsgálatokon túl kapunk 3 ábrát (a reziduumok eloszlását bemutató hisztogram a normalitás ellenőrzésére, a reziduum-becsült érték ábra a linearitás és szóráshomogenitás ellenőrzésére, valamint a szokásos szórásdiagram a regressziós egyenessel). Ezen túl torzító pontok keresését is elvégezhetjük a Cook-távolság által csökkenő sorrendbe állított táblázat segítségével, amely tartalmazza még a becsült értékeket, a közönséges reziduumokat, a studentizált reziduumokat és a DFFITS értékeket. Az X1.new= argumentummal becslést is végezhetünk, melynek eredménye a becsült érték mellett a becslés standard hibája, a predikciós intervallum határai és annak mérete.
library(lessR)
Regression(ONGYILK ~ GDP, data = d, X1.new = c(2000, 10000))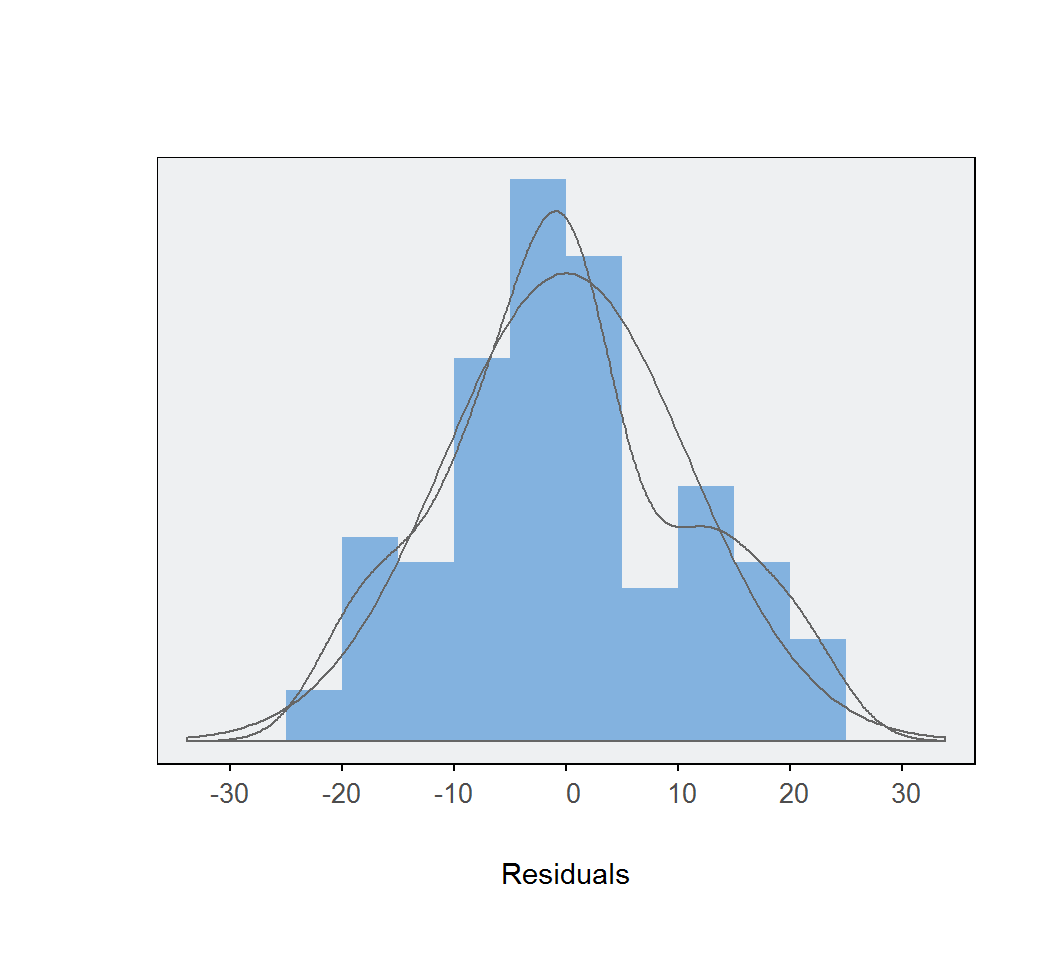

## BACKGROUND
##
## Data Frame: d
##
## Response Variable: ONGYILK
## Predictor Variable: GDP
##
## Number of cases (rows) of data: 100
## Number of cases retained for analysis: 100
##
##
## BASIC ANALYSIS
##
## Estimate Std Err t-value p-value Lower 95% Upper 95%
## (Intercept) 22.4807127 2.5462232 8.829 0.000 17.4278156 27.5336098
## GDP 0.0025860 0.0003814 6.780 0.000 0.0018291 0.0033429
##
##
## Standard deviation of residuals: 10.9359006 for 98 degrees of freedom
##
## R-squared: 0.319 Adjusted R-squared: 0.312 PRESS R-squared: 0.291
##
## Null hypothesis that all population slope coefficients are 0:
## F-statistic: 45.972 df: 1 and 98 p-value: 0.000
##
##
## df Sum Sq Mean Sq F-value p-value
## Model 1 5497.9382205 5497.9382205 45.9717195 0.000
## Residuals 98 11720.2043105 119.5939215
## ONGYILK 99 17218.1425309 173.9206316
##
##
## RELATIONS AMONG THE VARIABLES
##
## ONGYILK GDP
## ONGYILK 1.00 0.57
## GDP 0.57 1.00
##
##
## RESIDUALS AND INFLUENCE
##
## Data, Fitted, Residual, Studentized Residual, Dffits, Cook's Distance
## [sorted by Cook's Distance]
## [res.rows = 20, out of 100 rows of data, or do res.rows="all"]
## ------------------------------------------------------------------------------------
## GDP ONGYILK fitted resid rstdnt dffits cooks
## 2 1410 47.0141940 26.1270203 20.8871738 1.9737796 0.3811468 0.0705500
## 96 10732 30.8032587 50.2340267 -19.4307680 -1.8321523 -0.3586577 0.0628100
## 93 10665 69.1737027 50.0607624 19.1129402 1.8004379 0.3486584 0.0594200
## 7 1558 43.9136226 26.5097532 17.4038694 1.6331885 0.3078545 0.0465900
## 90 9383 25.9282414 46.7454672 -20.8172258 -1.9540237 -0.3043507 0.0450200
## 6 1766 9.6539464 27.0476483 -17.3937019 -1.6302929 -0.2969096 0.0433400
## 78 8311 67.2846841 43.9732390 23.3114451 2.1905271 0.2822881 0.0383600
## 11 2385 46.1234088 28.6484031 17.4750057 1.6329711 0.2675886 0.0352000
## 85 9751 30.6582924 47.6971276 -17.0388352 -1.5917245 -0.2644078 0.0344200
## 14 2766 11.3840772 29.6336820 -18.2496048 -1.7045994 -0.2612445 0.0334700
## 91 10487 35.6244309 49.6004484 -13.9760176 -1.3050663 -0.2454977 0.0299200
## 30 3527 51.0089286 31.6016537 19.4072750 1.8111888 0.2425162 0.0287400
## 36 4574 12.5400950 34.3092310 -21.7691359 -2.0351030 -0.2296550 0.0255500
## 42 5299 59.3739377 36.1841054 23.1898323 2.1719620 0.2253236 0.0244600
## 88 9707 61.9958982 47.5833421 14.4125561 1.3411312 0.2210867 0.0242400
## 67 7294 63.1047336 41.3432427 21.7614909 2.0336845 0.2236281 0.0242300
## 63 7701 23.0541209 42.3957585 -19.3416376 -1.8008715 -0.2098882 0.0215300
## 17 2566 15.6394705 29.1164752 -13.4770047 -1.2513958 -0.1986726 0.0196200
## 1 1592 15.4808453 26.5976784 -11.1168331 -1.0346215 -0.1939384 0.0187900
## 73 8344 59.4397789 44.0585781 15.3812007 1.4257030 0.1847792 0.0168900
##
##
## FORECASTING ERROR
##
## Data, Predicted, Standard Error of Forecast, 95% Prediction Intervals
## [sorted by lower bound of prediction interval]
## --------------------------------------------------------------------------------
## GDP ONGYILK pred sf pi:lwr pi:upr width
## 1 2000.0000000 27.6527802 11.0973423 5.6304656 49.6750947 44.0446291
## 2 10000.0000000 48.3410500 11.0943248 26.3247236 70.3573764 44.0326528
##
##
## ---------------------------------------
## Plot 1: Distribution of Residuals
## Plot 2: Residuals vs Fitted Values
## Plot 3: Scatterplot and Regression Line
## ---------------------------------------library(DescTools)
DurbinWatsonTest(formula = lm.1) # a hipotézisvizsgálat a reziduumok függetlenségéről##
## Durbin-Watson test
##
## data: lm.1
## DW = 2.5457, p-value = 0.996
## alternative hypothesis: true autocorrelation is greater than 0library(lmSupport)
lm.0 <- lm(formula = ONGYILK ~ 1, data = d)
modelCompare(lm.0, lm.1) # R^2 változása a nullmodellhez képest## SSE (Compact) = 17218.14
## SSE (Augmented) = 11720.2
## Delta R-Squared = 0.3193108
## Partial Eta-Squared (PRE) = 0.3193108
## F(1,98) = 45.97172, p = 0.00000000090947097.1.2 Példa: problémás esetek
Vizsgáljuk meg, hogy az egyszerű lineáris regressziós elemzés folyamán a nem lineáris kapcsolatok és torzító pontok jelenlétére hol bukkanhatunk rá. Forrás: (Moksony 2006, 51), http://www.bkae.hu/moksony
Adatok beolvasása. Olvassuk be az adatokat egy d.1 és egy d.2 nevű adattáblába:
d.1 <- read.table(file = textConnection("
X Y
1 286
-6 181
2 281
6 211,01
-9 61
8 146,001
-4 236
9 105,979
-7 146
10 61,01
3 271
-8 106
4 256
11 11
-1 281
5 236
-2 271
7 172,915
-3 256
-5 211
-10 11
"), header=T, sep="", dec = ",")
str(d.1) # az adattábla szerkezete## 'data.frame': 21 obs. of 2 variables:
## $ X: int 1 -6 2 6 -9 8 -4 9 -7 10 ...
## $ Y: num 286 181 281 211 61 ...d.1 # a beolvasott adattábla## X Y
## 1 1 286.000
## 2 -6 181.000
## 3 2 281.000
## 4 6 211.010
## 5 -9 61.000
## 6 8 146.001
## 7 -4 236.000
## 8 9 105.979
## 9 -7 146.000
## 10 10 61.010
## 11 3 271.000
## 12 -8 106.000
## 13 4 256.000
## 14 11 11.000
## 15 -1 281.000
## 16 5 236.000
## 17 -2 271.000
## 18 7 172.915
## 19 -3 256.000
## 20 -5 211.000
## 21 -10 11.000d.2 <- read.table(file = textConnection("
X Y
1 6
2 6
3 6
4 6
5 6
6 6
7 6
8 6
9 6
10 6
18 22
"), header=T, sep="", dec = ",")
str(d.2) # az adattábla szerkezete## 'data.frame': 11 obs. of 2 variables:
## $ X: int 1 2 3 4 5 6 7 8 9 10 ...
## $ Y: int 6 6 6 6 6 6 6 6 6 6 ...d.2 # a beolvasott adattábla## X Y
## 1 1 6
## 2 2 6
## 3 3 6
## 4 4 6
## 5 5 6
## 6 6 6
## 7 7 6
## 8 8 6
## 9 9 6
## 10 10 6
## 11 18 22Önmagában a regressziós hipotézisvizsgálatok nem fedik fel a problémát.
lm.1 <- lm(Y ~ X, data = d.1)
summary(lm.1)##
## Call:
## lm(formula = Y ~ X, data = d.1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -169.85 -74.85 30.15 75.15 105.15
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 180.85309526627 20.50589296917 8.82 0.0000000382
## X -0.00000005379 3.14810697500 0.00 1
##
## Residual standard error: 93.67 on 19 degrees of freedom
## Multiple R-squared: 1.537e-17, Adjusted R-squared: -0.05263
## F-statistic: 2.92e-16 on 1 and 19 DF, p-value: 1lm.2 <- lm(Y ~ X, data = d.2)
summary(lm.2)##
## Call:
## lm(formula = Y ~ X, data = d.2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.1781 -2.1538 -0.1296 1.8947 5.3441
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.0810 1.6514 1.260 0.23932
## X 0.8097 0.2057 3.936 0.00342
##
## Residual standard error: 3.082 on 9 degrees of freedom
## Multiple R-squared: 0.6326, Adjusted R-squared: 0.5918
## F-statistic: 15.5 on 1 and 9 DF, p-value: 0.003424Első esetben a modell nem szignifikáns (\(F(1, 19)<0,0001; p = 1\)), míg a második esetben igen (\(F(1, 9)=15,5; p = 0,0034\)). Ez valóban azt jelenti, hogy az első esetben nincs kapcsolat a két változó között, míg a másik esetben pedig azt, hogy van?
Rajzoljuk meg a 6 diganosztikus ábrát az első (lm.1) modell esetén.
par(mfrow=c(2,3))
plot(lm.1, which = 1)
plot(lm.1, which = 2)
plot(lm.1, which = 3)
plot(lm.1, which = 4)
plot(lm.1, which = 5)
plot(lm.1, which = 6)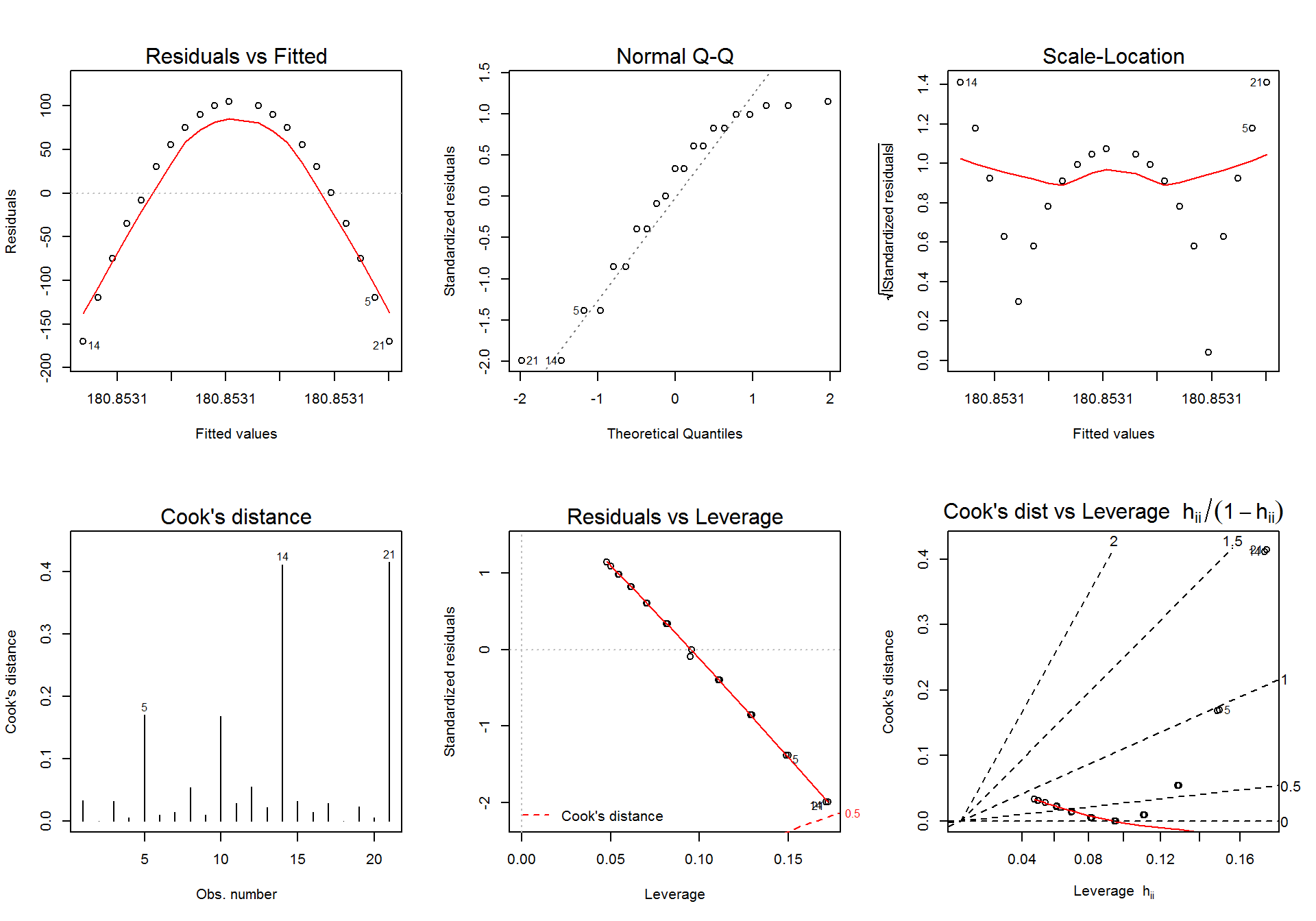
par(mfrow=c(1,1))Az első illesztett modell diagnosztikus ábrái alapján arra következtethetünk, hogy nincs lineáris kapcsolat a két változó között (1. ábra), a reziduumok normalitása sérülhet (2. ábra), a reziduumok szórása nem stabil (3. ábra) és gyanús torzító pontok is megjelennek (4-6. ábra). Ezek közül a legsúlyosabb probléma az \(X\) és \(Y\) változó lineáris kapcsolatának megsértése (1. ábra), így a lineáris regresszió egyik alkalmazási feltétele nem teljesül. Ha megrajzoljuk a két változó kapcsolatát leíró szórásdiagramot, akkor világossá válik, hogy a két változó között erős, de nem lineáris kapcsolat áll fenn.
library(car)
scatterplot(x = d.1$X, y = d.1$Y, spread = F)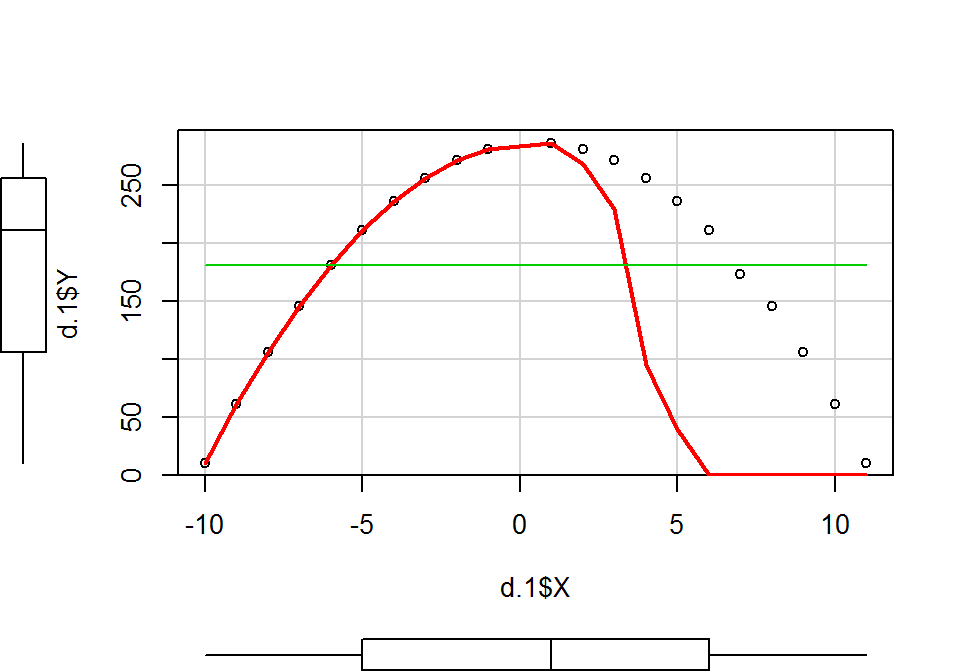
Rajzoljuk meg a 6 diganosztikus ábrát a második (lm.2) modell esetén.
par(mfrow=c(2,3))
plot(lm.2, which = 1)
plot(lm.2, which = 2)
plot(lm.2, which = 3)
plot(lm.2, which = 4)
plot(lm.2, which = 5)
plot(lm.2, which = 6)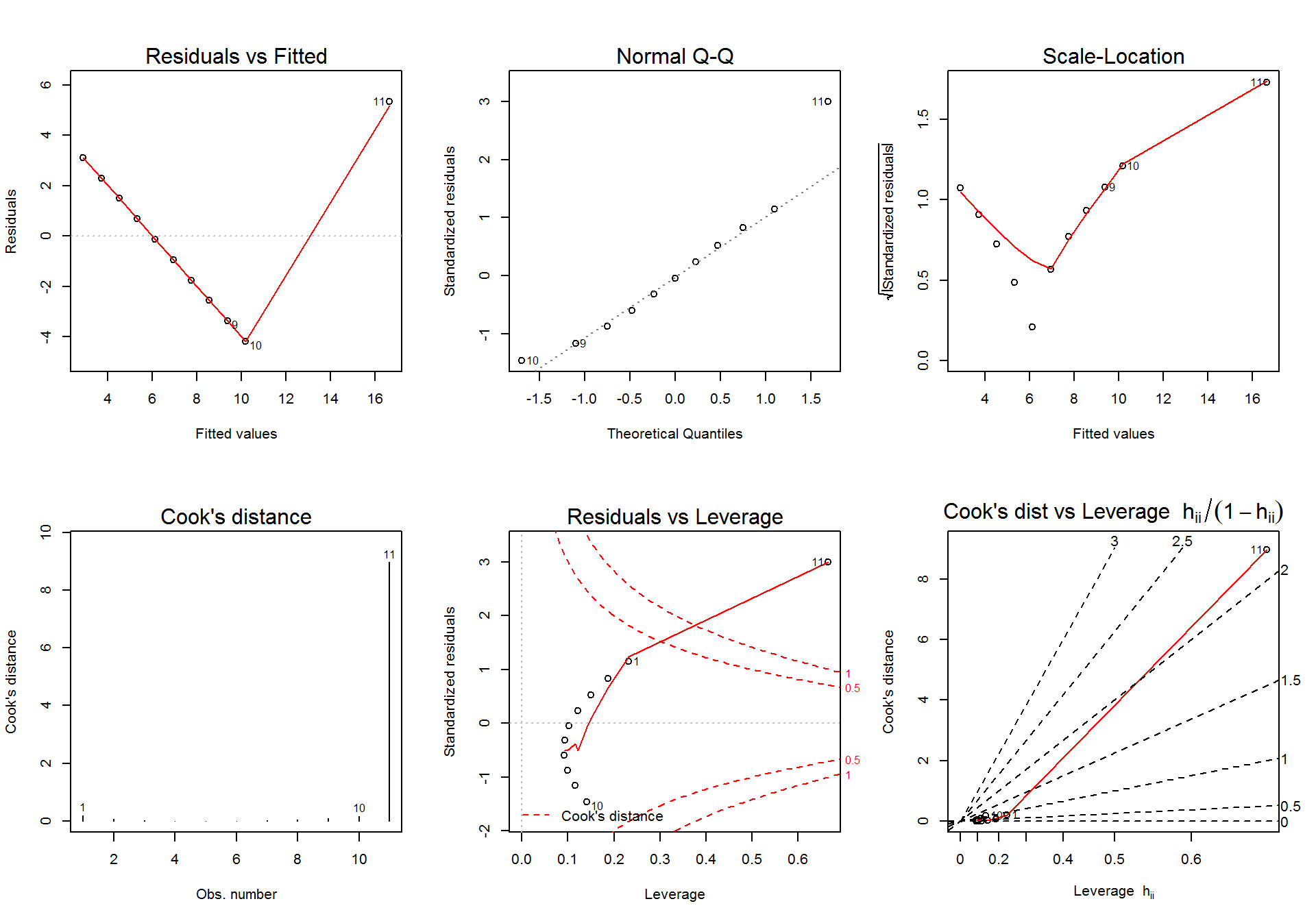
par(mfrow=c(1,1))A fenti ábrákról leolvasható a linearitás hiánya (1. ábra), a reziduumok normalitásának sérülése (2. ábra), a reziduumok szórásának heterogenitása, és különösen feltünő a 11. adatpont rendkívül nagy Cook-féle távolság értéke, ami egyértelműen jelzi, hogy torzító pontról van szó. Ha megrajzoljuk a két változó kapcsolatát leíró szórásdiagramot, akkor világossá válik, hogy a két változó között nincs kapcsolat, csupán az egyetlen torzító pont hatásának köszönhető a szignifikáns modell.
library(car)
scatterplot(x = d.2$X, y = d.2$Y, spread = F)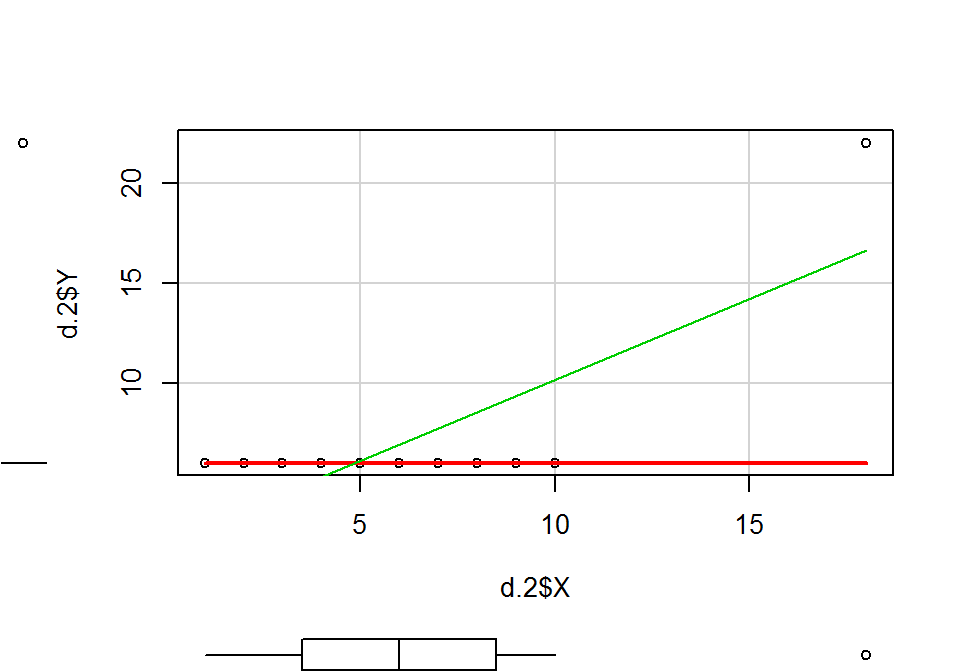
A fenti összefüggések az influence.measures() és influenceIndexPlot() segítségével is megmutathatók.
influence.measures(lm.1)## Influence measures of
## lm(formula = Y ~ X, data = d.1) :
##
## dfb.1_ dfb.X dffit cov.r cook.d hat inf
## 1 0.257256 0.01904 0.260326 1.013 0.033275669 0.0479
## 2 0.000397 -0.00037 0.000522 1.232 0.000000144 0.0957
## 3 0.241702 0.05616 0.253323 1.029 0.031723629 0.0501
## 4 0.069367 0.06298 0.097689 1.199 0.005006740 0.0815
## 5 -0.376031 0.49482 -0.598865 1.059 0.170090038 0.1501
## 6 -0.080689 -0.10276 -0.136102 1.233 0.009696304 0.1108
## 7 0.143087 -0.09470 0.165650 1.152 0.014197839 0.0707
## 8 -0.177247 -0.25948 -0.326854 1.182 0.054207842 0.1288
## 9 -0.097360 0.10351 -0.136725 1.234 0.009785253 0.1116
## 10 -0.296243 -0.49168 -0.596010 1.058 0.168498035 0.1491
## 11 0.214484 0.08467 0.237610 1.060 0.028261151 0.0545
## 12 -0.219268 0.26114 -0.328269 1.183 0.054676880 0.1297
## 13 0.176334 0.09899 0.209727 1.103 0.022376678 0.0613
## 14 -0.453227 -0.84348 -0.992337 0.842 0.411136946 0.1716 *
## 15 0.250925 -0.05799 0.253776 1.029 0.031836670 0.0502
## 16 0.127870 0.09365 0.164995 1.152 0.014085987 0.0703
## 17 0.228300 -0.08633 0.238265 1.060 0.028416671 0.0548
## 18 -0.018234 -0.01984 -0.028099 1.230 0.000416538 0.0950
## 19 0.192443 -0.10039 0.210456 1.103 0.022532272 0.0616
## 20 0.079566 -0.06355 0.098074 1.199 0.005046249 0.0821
## 21 -0.590106 0.84863 -0.997137 0.842 0.414974472 0.1727 *influence.measures(lm.2)## Influence measures of
## lm(formula = Y ~ X, data = d.2) :
##
## dfb.1_ dfb.X dffit cov.r cook.d hat
## 1 0.6448 -0.50468 0.6468 1.20e+00 0.200667 0.2324
## 2 0.3828 -0.27836 0.3887 1.33e+00 0.078516 0.1866
## 3 0.2016 -0.13211 0.2107 1.40e+00 0.024209 0.1498
## 4 0.0749 -0.04181 0.0830 1.42e+00 0.003848 0.1219
## 5 -0.0115 0.00482 -0.0142 1.41e+00 0.000113 0.1028
## 6 -0.0652 0.01352 -0.0970 1.36e+00 0.005229 0.0927
## 7 -0.0899 -0.01458 -0.1817 1.29e+00 0.017846 0.0915
## 8 -0.0858 -0.08265 -0.2861 1.18e+00 0.042117 0.0992
## 9 -0.0497 -0.19937 -0.4301 1.03e+00 0.088435 0.1158
## 10 0.0271 -0.38264 -0.6408 8.56e-01 0.176044 0.1413
## 11 -122722348.8893 203565920.03544 219065684.5947 4.19e-31 8.972727 0.6660
## inf
## 1
## 2
## 3
## 4
## 5
## 6
## 7
## 8
## 9
## 10
## 11 *library(car)
influenceIndexPlot(lm.1)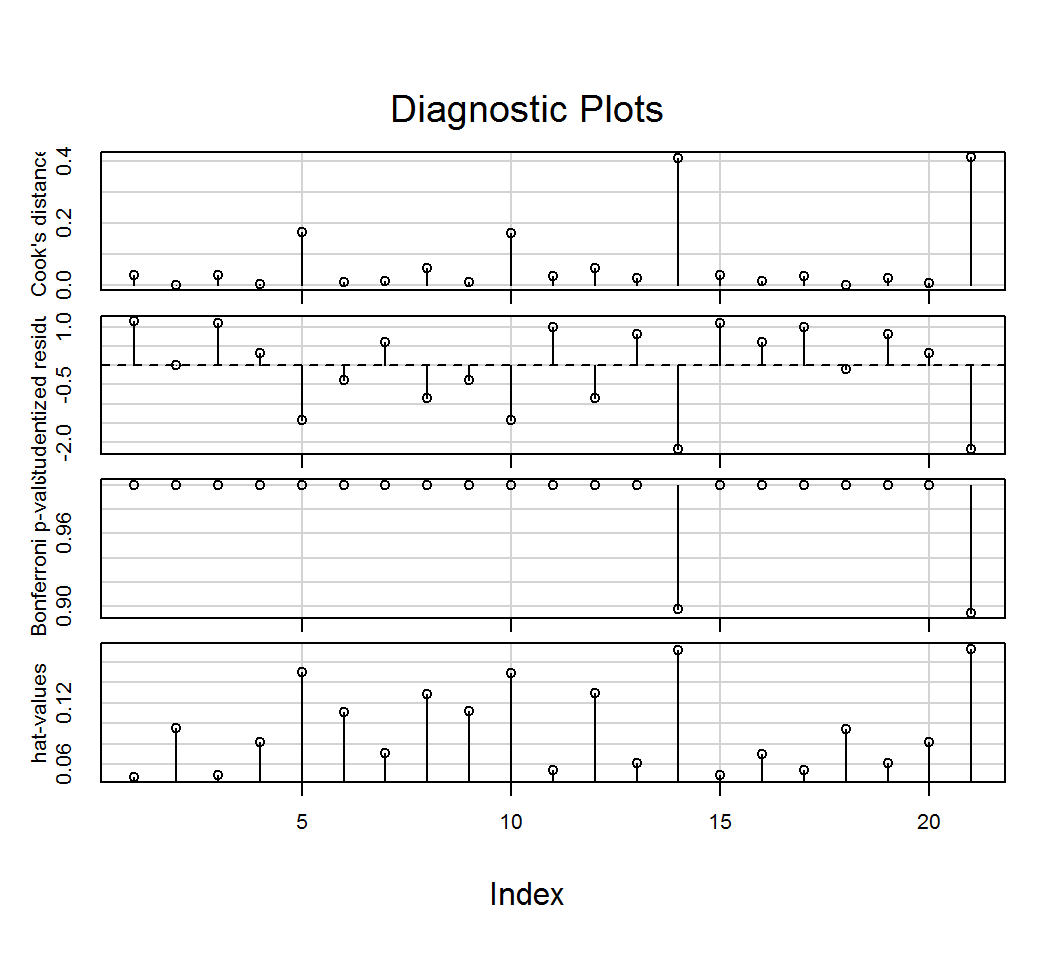
influenceIndexPlot(lm.2)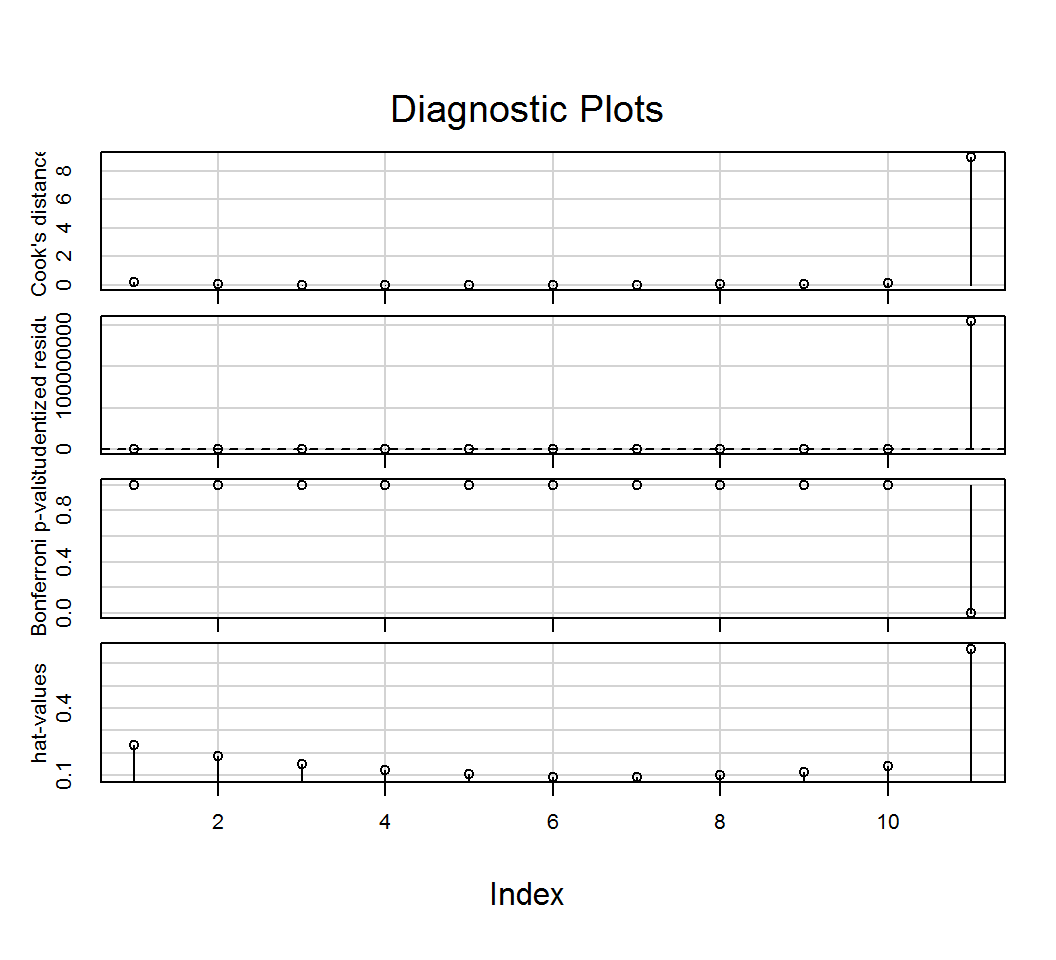
7.2 Mediátor
library(foreign)
#d <- read.spss(file = "data/Lambert et al. (2012).sav", to.data.frame = T)7.3 Többszörös lineáris regresszió
A többszörös lineáris regresszió a folytonos \(Y\) függő változó és több folytonos \(X_1, X_2, \dots , X_r\) magyarázó változó között keresi a lineáris kapcsolat formáját: \(y_i=\beta_0+\beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_r x_{ir} +\varepsilon_i\).
Alkalmazási feltételek:
- lineáris kapcsolat a magyarázóváltozók és
Yközött - a reziduumok (\(\varepsilon_i\)) függetlenek és normális eloszlásúak, 0 várható értékkel állandó szórással: \(\varepsilon_i \sim N(0,\sigma)\)
- multikollinearitás hiánya
- a magyarázóváltozók száma kevesebb legyen, mint a mintaelemek száma
Null- és ellenhipotézisek:
- A tengelymetszetre:
- Nullhipotézis:
- \(H_0:\beta_0=0\)
- Ellenhipotézis:
- \(H_1:\beta_0 \neq 0\)
- Nullhipotézis:
- Az egyes magyarázó változókra:
- Nullhipotézis:
- \(H_0^i:\beta_i=0\), ahol \(i=1, 2, \dots, r\)
- Ellenhipotézis:
- \(H_0^i:\beta_i \neq 0\), ahol \(i=1, 2, \dots, r\)
- Nullhipotézis:
- A teljes modellre:
- Nullhipotézis:
- \(H_0:\) Az \(Y\) változó nem függ egyik \(X_i\)-től sem
- Ellenhipotézis:
- \(H_1:\) Az \(Y\) változó függ valamelyik \(X_i\)-től
- Nullhipotézis:
Próbastatisztika:
A próbastatisztika az egyes paraméterekre:
\[T_{\beta_i}=\frac{b_i}{SE_{b_i}} \sim t(n-r-1), i=0, 1, 2, \dots , r\]
Az \(Y\) teljes szórása \(SS_Y\) (SS - sum of squares, eltérés négyzetösszeg), az \(X_i\)-ktől való függésből eredő szórás \(SS_R\), a véletlen hiba \(SS_H\):
\[SS_T=SS_R+SS_H\]
A próbastatisztika a teljes modellre:
\[F=\frac{SS_R/r}{SS_H/(n-r-1)} \sim F(r,n-r-1)\]
library(foreign)
d <- read.spss(file = "data/gyogyszertar-konyv.sav", to.data.frame = T, use.value.labels = F)
d <- d[, c("k37", "k5_1", "k5_5", "k19_1")]
names(d) <- c("forgalom", "jarokelok", "korhaz", "verseny")
d <- d[d$forgalom < 22040,]
lm.1 <- lm(forgalom ~ jarokelok + korhaz + verseny, data = d)
summary(lm.1)##
## Call:
## lm(formula = forgalom ~ jarokelok + korhaz + verseny, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8549.3 -2712.4 -395.7 2564.6 12788.6
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1494.1 1399.0 1.068 0.2873
## jarokelok 480.1 283.3 1.695 0.0922
## korhaz 1327.5 214.0 6.203 0.00000000519
## verseny 663.1 278.0 2.385 0.0183
##
## Residual standard error: 4496 on 149 degrees of freedom
## (13 observations deleted due to missingness)
## Multiple R-squared: 0.2592, Adjusted R-squared: 0.2443
## F-statistic: 17.38 on 3 and 149 DF, p-value: 0.0000000009925lm.2 <- lm(forgalom ~ korhaz + verseny, data = d)
summary(lm.2)##
## Call:
## lm(formula = forgalom ~ korhaz + verseny, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8159.4 -3011.1 -409.4 2440.7 13747.3
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2947.9 1101.0 2.677 0.00824
## korhaz 1383.1 209.6 6.600 0.000000000657
## verseny 640.6 277.9 2.306 0.02250
##
## Residual standard error: 4517 on 151 degrees of freedom
## (12 observations deleted due to missingness)
## Multiple R-squared: 0.2426, Adjusted R-squared: 0.2325
## F-statistic: 24.18 on 2 and 151 DF, p-value: 0.0000000007782lm.3 <- lm(forgalom ~ korhaz, data = d)
summary(lm.3)##
## Call:
## lm(formula = forgalom ~ korhaz, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8832.1 -3082.8 -333.5 2635.5 13666.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4958.9 681.3 7.279 0.0000000000168
## korhaz 1374.6 212.5 6.469 0.0000000012768
##
## Residual standard error: 4580 on 152 degrees of freedom
## (12 observations deleted due to missingness)
## Multiple R-squared: 0.2159, Adjusted R-squared: 0.2107
## F-statistic: 41.85 on 1 and 152 DF, p-value: 0.000000001277anova(lm.2, lm.3)## Analysis of Variance Table
##
## Model 1: forgalom ~ korhaz + verseny
## Model 2: forgalom ~ korhaz
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 151 3080536462
## 2 152 3188975118 -1 -108438657 5.3154 0.0225anova(lm.2, lm.3)## Analysis of Variance Table
##
## Model 1: forgalom ~ korhaz + verseny
## Model 2: forgalom ~ korhaz
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 151 3080536462
## 2 152 3188975118 -1 -108438657 5.3154 0.0225s1 <- step(lm.1, direction = "forward")## Start: AIC=2577.72
## forgalom ~ jarokelok + korhaz + versenysummary(s1)##
## Call:
## lm(formula = forgalom ~ jarokelok + korhaz + verseny, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8549.3 -2712.4 -395.7 2564.6 12788.6
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1494.1 1399.0 1.068 0.2873
## jarokelok 480.1 283.3 1.695 0.0922
## korhaz 1327.5 214.0 6.203 0.00000000519
## verseny 663.1 278.0 2.385 0.0183
##
## Residual standard error: 4496 on 149 degrees of freedom
## (13 observations deleted due to missingness)
## Multiple R-squared: 0.2592, Adjusted R-squared: 0.2443
## F-statistic: 17.38 on 3 and 149 DF, p-value: 0.0000000009925drop1(object = lm.1, test = "F")## Single term deletions
##
## Model:
## forgalom ~ jarokelok + korhaz + verseny
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 3012362800 2577.7
## jarokelok 1 58061082 3070423882 2578.6 2.8719 0.09223
## korhaz 1 777982778 3790345578 2610.9 38.4812 0.000000005188
## verseny 1 115004523 3127367323 2581.4 5.6884 0.01833#library(lessR)
#Regression(forgalom ~ jarokelok + korhaz + verseny, data = d)
library(userfriendlyscience)
regr(forgalom ~ jarokelok + korhaz + verseny, dat = d)## Regression analysis for formula: forgalom ~ jarokelok + korhaz + verseny
##
## Significance test of the entire model (all predictors together):
## Multiple R-squared: [0.14, 0.38] (point estimate = 0.26, adjusted = 0.24)
## Test for significance: F[3, 149] = 17.38, p < .001
##
## Raw regression coefficients (unstandardized beta values, called 'B' in SPSS):
##
## 95% conf. int. estimate se t p
## (Intercept) [-1270.32; 4258.51] 1494.09 1398.99 1.07 .287
## jarokelok [-79.71; 1039.98] 480.13 283.32 1.69 .092
## korhaz [904.63; 1750.35] 1327.49 214.00 6.20 <.001
## verseny [113.71; 1212.4] 663.05 278.00 2.39 .018
##
## Scaled regression coefficients (standardized beta values, called 'Beta' in SPSS):
##
## 95% conf. int. estimate se t p
## (Intercept) [-0.14; 0.14] 0.00 0.07 0.06 .950
## jarokelok [-0.02; 0.27] 0.12 0.07 1.69 .092
## korhaz [0.31; 0.59] 0.45 0.07 6.20 <.001
## verseny [0.03; 0.31] 0.17 0.07 2.39 .018# variancia infláció faktor (VIF) a multikollinearitás vizsgálatára
library(car)
vif(lm.1)## jarokelok korhaz verseny
## 1.046317 1.040390 1.005826vif(lm.2)## korhaz verseny
## 1.000305 1.0003057.4 Polinomiális regresszió
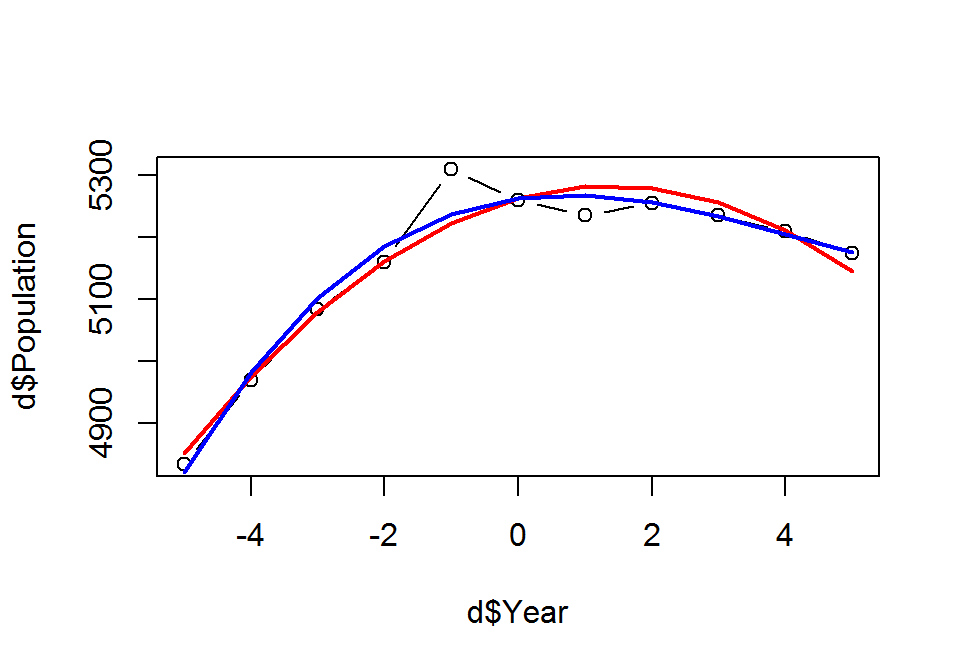
http://www.r-bloggers.com/polynomial-regression-techniques/
Year <- c(1959, 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969)
Population <- c(4835, 4970, 5085, 5160, 5310, 5260, 5235, 5255, 5235, 5210, 5175)
d <- data.frame(Year, Population)
d## Year Population
## 1 1959 4835
## 2 1960 4970
## 3 1961 5085
## 4 1962 5160
## 5 1963 5310
## 6 1964 5260
## 7 1965 5235
## 8 1966 5255
## 9 1967 5235
## 10 1968 5210
## 11 1969 5175d$Year <- d$Year - 1964
d## Year Population
## 1 -5 4835
## 2 -4 4970
## 3 -3 5085
## 4 -2 5160
## 5 -1 5310
## 6 0 5260
## 7 1 5235
## 8 2 5255
## 9 3 5235
## 10 4 5210
## 11 5 5175plot(d$Year, d$Population, type="b")
lm.1 <- lm(Population ~ Year, data = d)
lm.2 <- lm(Population ~ Year + I(Year^2), data = d)
lm.3 <- lm(Population ~ Year + I(Year^2) + I(Year^3), data = d)
summary(lm.1)##
## Call:
## lm(formula = Population ~ Year, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -175.68 -67.27 15.68 54.89 182.04
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5157.27 33.06 155.988 <2e-16
## Year 29.32 10.46 2.804 0.0206
##
## Residual standard error: 109.7 on 9 degrees of freedom
## Multiple R-squared: 0.4663, Adjusted R-squared: 0.407
## F-statistic: 7.863 on 1 and 9 DF, p-value: 0.02057summary(lm.2)##
## Call:
## lm(formula = Population ~ Year + I(Year^2), data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -46.888 -18.834 -3.159 2.040 86.748
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5263.159 17.655 298.110 < 2e-16
## Year 29.318 3.696 7.933 0.0000464
## I(Year^2) -10.589 1.323 -8.002 0.0000436
##
## Residual standard error: 38.76 on 8 degrees of freedom
## Multiple R-squared: 0.9407, Adjusted R-squared: 0.9259
## F-statistic: 63.48 on 2 and 8 DF, p-value: 0.00001235summary(lm.3)##
## Call:
## lm(formula = Population ~ Year + I(Year^2) + I(Year^3), data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.774 -14.802 -1.253 3.199 72.634
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5263.1585 15.0667 349.324 4.16e-16
## Year 14.3638 8.1282 1.767 0.1205
## I(Year^2) -10.5886 1.1293 -9.376 3.27e-05
## I(Year^3) 0.8401 0.4209 1.996 0.0861
##
## Residual standard error: 33.08 on 7 degrees of freedom
## Multiple R-squared: 0.9622, Adjusted R-squared: 0.946
## F-statistic: 59.44 on 3 and 7 DF, p-value: 0.00002403anova(lm.1, lm.2)## Analysis of Variance Table
##
## Model 1: Population ~ Year
## Model 2: Population ~ Year + I(Year^2)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 9 108217
## 2 8 12020 1 96197 64.026 0.00004361anova(lm.2, lm.3)## Analysis of Variance Table
##
## Model 1: Population ~ Year + I(Year^2)
## Model 2: Population ~ Year + I(Year^2) + I(Year^3)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 8 12019.8
## 2 7 7659.5 1 4360.3 3.9848 0.0861anova(lm.1, lm.2)## Analysis of Variance Table
##
## Model 1: Population ~ Year
## Model 2: Population ~ Year + I(Year^2)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 9 108217
## 2 8 12020 1 96197 64.026 0.00004361plot(d$Year, d$Population, type="b")
points(d$Year, predict(lm.2), type="l", col="red", lwd=2)
points(d$Year, predict(lm.3), type="l", col="blue", lwd=2)