3 Egy- és kétmintás próbák a várható értékre
Ebben a fejezetben olyan statisztikai változókat vizsgálunk, amelyek a normális eloszlásúak és a normális eloszlás egyik paraméterére, a várható értékre vonatkozóan fogalmazunk meg hipotézist. Az egymintás próbákban azt vizsgáljuk, hogy az \(X\) változó értékei általában kisebbek-e vagy nagyobbak-e, mint egy bizonyos hipotetikus érték, míg a páros és független mintás próbákban két változó ugyanakkoraságát vizsgáljuk. Ezek a kérdések mind visszavezethetők a változó(k) középértékére, esetünkben a várható értékére vonatkozó hipotézis megfogalmazására. Az egymintás próbákban azt vizsgáljuk, hogy a várható érték eltér-e egy hipotetikus értéktől. A páros mintás próbákban a változó két különböző helyzetre vagy időpontra vonatkozó várható értékének eltérését vizsgáljuk. A független mintás esetekben pedig a változó két különböző populációbeli várható értékének eltérését vizsgáljuk.
3.1 Egymintás u-próba
Az egymintás u-próba egy ismert \(\sigma\) szórású normális eloszlású változó várható értékére vonatkozó hipotézist teszteli: a \(\mu\) várható érték eltér-e egy előre definiált \(\mu_0\) értéktől.
Alkalmazási feltételek:
- a minta változója a populációban normális eloszlású
- a minta változójának a szórása (\(\sigma\)) ismert a populációban
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu=\mu_0\)
- Ellenhipotézis:
- \(H_1: \mu \neq \mu_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu < \mu_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu > \mu_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
A nullhipotézis igaz volta mellett a \(Z\) próbastatisztika standard normális eloszlású.
\[Z=\frac{\bar{X}-\mu_0}{\sigma / \sqrt{n}} \sim N(0,1)\]
3.1.1 Példa kétoldali ellenhipotézisre: földrengés hatása a szorongásra.
Tegyük fel, hogy a szorongás mértéke a populációban normális eloszlású változó \(\mu=50\) és \(\sigma=10\). Egy földrengés után egy véletlen minta adatai a szorongásra a következők: 72, 59, 54, 56, 48, 52, 57, 51, 64, 67. Van hatása a földrengésnek a szorongás szintjére?
Forrás: (Cohen 2013, 162)
A feladat szövegéből kiderül, hogy az egymintás u-próba feltételei teljesülnek. A földrengés hatására a szorongás szintje megváltozhatott, így azt teszteljük, hogy az új, ismeretlen szorongásváltozó várható értéke eltér-e a korábbi 50-es szinttől. Vagyis a következő null- és ellenhipotézist vizsgáljuk:
- \(H_0: \mu=50\)
- \(H_1: \mu \neq 50\) (kétoldali ellenhipotézis)
Adatok beolvasása. Az egymintás u-próba végrehajtása előtt létrehozzuk x vektorban a mintát.
# az adatvektor létrehozása
x <- c(72, 59, 54, 56, 48, 52, 57, 51, 64, 67) Az egymintás u-próba végrehajtása. A próba végrehajtásához a PASWR2 csomag z.test() függvényét hívjuk. Az argumentumokban megadjuk az adatmintát (x= argumentum), a hipotetikus várható értéket (mu=), és az ismert populációbeli szórást (sigma.x=).
library(PASWR2)
PASWR2::z.test(x = x, mu = 50, sigma.x = 10)##
## One Sample z-test
##
## data: x
## z = 2.5298, p-value = 0.01141
## alternative hypothesis: true mean is not equal to 50
## 95 percent confidence interval:
## 51.80205 64.19795
## sample estimates:
## mean of x
## 58Az egymintás u-próba értékelése. Az egymintás u-próba eredménye alapján azt mondhatjuk, hogy a földrengés hatására szignifikánsan megnő a szorongás szintje (\(z=2,5298\); \(p = 0,0114\)).
Az egymintás u-próba kézi számolása. A próba outputjában szereplő értékeket a fent megadott próbastatisztika alapján magunk is kiszámolhatjuk:
atlag <- mean(x, na.rm = T) # mintaátlag
szoras <- 10 # populációbeli szórás
n <- sum(!is.na(x)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
mu.0 <- 50 # hipotetikus várható érték
z <- (atlag-mu.0)/SE # próbastatisztika értéke
z # próbastatisztika értékének kiírása## [1] 2.5298222*(1-pnorm(q = abs(z))) # a p érték kétoldali próba esetén## [1] 0.01141204Az egymintás u-próbához kapcsolódó konfidenciaintervallum. A próba outputjában szereplő konfidenciaintervallum határait a DescTools csomag MeanCI() függvényével is meghatározhatjuk, de a kézi kiszámolása sem túl bonyolult. Normális eloszlás és ismert \(\sigma\) szórás esetén a várható értékre vonatkozó \(\left(1-\alpha \right)\) megbízhatóságú konfidenciaintervallum:
\[\left] \bar{X}-u_{\alpha}\frac{\sigma}{\sqrt{n}}, \bar{X}+u_{\alpha}\frac{\sigma}{\sqrt{n}} \right[\]
A MeanCI() függvény argumentumában meg kell adnunk az adatmintát (x=), az ismert szórást (sd=), valamint opcionálisan a megbízhatósági szintet (conf.level=) és a hiányzó értékek eltávolítására használatos na.rm=T paramétert.
library(DescTools)
MeanCI(x = x, sd = 10, conf.level = 0.95, na.rm=T) # 95%-os konfidenciaintervallum## mean lwr.ci upr.ci
## 58.00000 51.80205 64.19795# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- mean(x, na.rm = T) # mintaátlag
szoras <- 10 # populációbeli szórás
n <- sum(!is.na(x)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
alfa <- 0.05 # alfa=1-0.95
u.alfa <- qnorm(p = 1-alfa/2) # u_alfa kritikusérték
atlag + c(-u.alfa*SE, u.alfa*SE) # a 95%-os konf.intv. határai ## [1] 51.80205 64.19795Az alkalmazási feltételek ellenőrzése az egymintás u-próbához. A példa szövege alapján feltételezhetjük a vizsgált szorongás változó normális eloszlását. Ha ez a kitétel hiányozna, akkor a shapiro.test() függvénnyel tesztelhetjük a minta mögötti változó normális eloszlását. A Shapiro-Wilk próba nullhipotézise szerint normális eloszlású a változó. A normalitás ellenőrzésére végezhetünk grafikus vizsgálatot, például rajzolhatunk hisztogramot vagy QQ-ábrát.
shapiro.test(x) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.95281, p-value = 0.7017par(mfrow=c(1,3)) # a grafikus eszköz felosztása 1 sorra és 3 oszlopra
hist(x) # normalitás ellenőrzése hisztogrammal
hist(x, freq = F); lines(density(x)) # normalitás ellenőrzése hisztogrammal, és simított gyakorásgi görbével
qqnorm(x);qqline(x) # normalitás ellenőrzése QQ-ábrával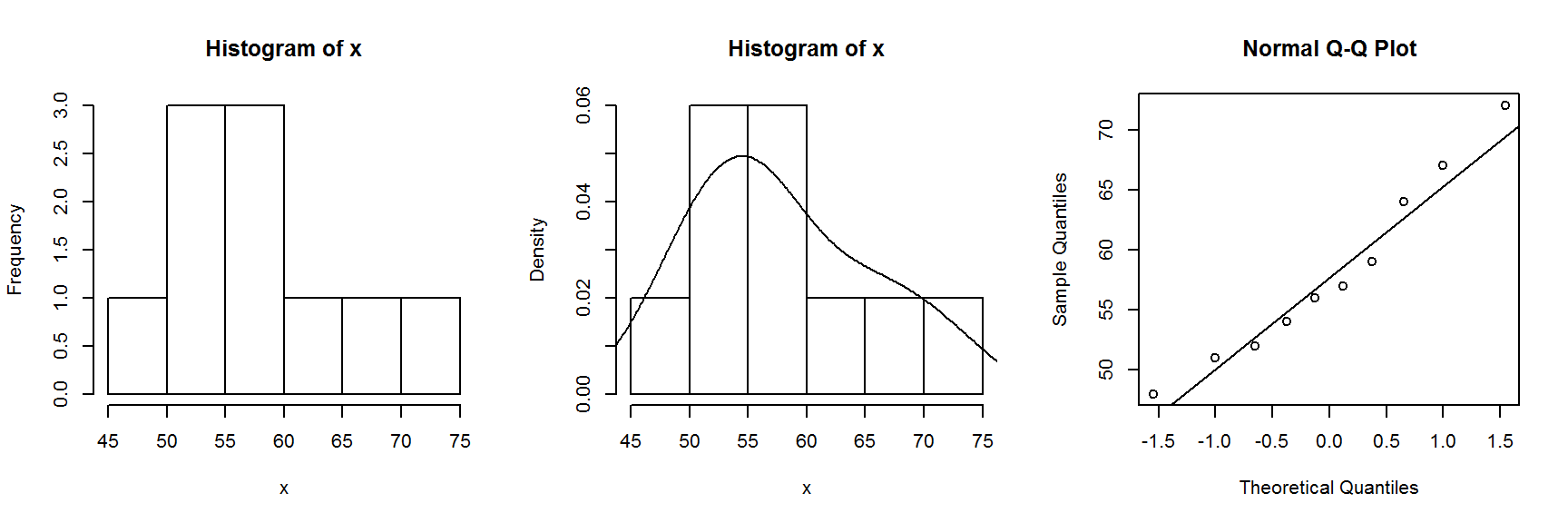
par(mfrow=c(1,1)) # az alapértelmezett felosztás visszaállítása a grafikus eszközönA Shapiro-Wilk próba eredménye nem cáfolja a változó normalitását (\(p=0,7017\)), és ugyanilyen következtetést vonhatunk le hisztogram és QQ-ábra alapján is.
Leíró statisztikák az egymintás u-próbához. Egyetlen változó esetén nagyon egyszerűen határozzuk meg a leíró statisztikai mutatókat. Az alapértelmezett summary() mellett számos csomagban találunk függvényt a mutatók kiírására. Most a psych csomag describe(), a DescTools csomag Desc() és pastecs csomag stat.desc() függvényére mutatunk példát:
summary(x) # mutatók a beépített summary() függvényével## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 48.00 52.50 56.50 58.00 62.75 72.00library(psych)
psych::describe(x = x) # mutatók a psych csomag describe() függvényével## vars n mean sd median trimmed mad min max range skew kurtosis se
## 1 1 10 58 7.6 56.5 57.5 7.41 48 72 24 0.47 -1.2 2.4library(DescTools)
Desc(x = x) # mutatók a DescTools csomag Desc() függvényével## --------------------------------------------------------------------------------------------------
## x (numeric)
##
## length n NAs unique 0s mean meanSE
## 10 10 0 = n 0 58.00 2.40
##
## .05 .10 .25 median .75 .90 .95
## 49.35 50.70 52.50 56.50 62.75 67.50 69.75
##
## range sd vcoef mad IQR skew kurt
## 24.00 7.60 0.13 7.41 10.25 0.47 -1.20
##
##
## level freq perc cumfreq cumperc
## 1 48 1 10.0% 1 10.0%
## 2 51 1 10.0% 2 20.0%
## 3 52 1 10.0% 3 30.0%
## 4 54 1 10.0% 4 40.0%
## 5 56 1 10.0% 5 50.0%
## 6 57 1 10.0% 6 60.0%
## 7 59 1 10.0% 7 70.0%
## 8 64 1 10.0% 8 80.0%
## 9 67 1 10.0% 9 90.0%
## 10 72 1 10.0% 10 100.0%library(pastecs)
print(stat.desc(x = x, norm=T), digits = 2) # mutatók a pastecs csomag stat.desc() függvényével## nbr.val nbr.null nbr.na min max range sum
## 10.00 0.00 0.00 48.00 72.00 24.00 580.00
## median mean SE.mean CI.mean.0.95 var std.dev coef.var
## 56.50 58.00 2.40 5.44 57.78 7.60 0.13
## skewness skew.2SE kurtosis kurt.2SE normtest.W normtest.p
## 0.47 0.34 -1.20 -0.45 0.95 0.70A hatás nagyságának meghatározása az egymintás u-próbában. Az egymintás u-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{\bar{X}-\mu_0}{\sigma}\right|\]
(mean(x)-50)/10 # Cohen-d kiszámítása## [1] 0.8A Cohen-d értéke 0.8, ami azt mutatja, hogy a hatás nagysága jelentős.
Az erő meghatározása egymintás u-próbában. A statisztikai erő meghatározásához a pwr csomag pwr.norm.test() függvényét használjuk. A bemenő paraméterek:
n=- a mintaelemszámd=- a hatás nagyságasig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formája
A statisztikai erő kiszámításához jelen esetben a populációbeli hatás méretéből (\(d=0,8\)) indulunk ki, de sokszor érdemesebb a legkisebb számunkra érdekes hatásból kiindulva elvégezni a számítást.
library(pwr)
d <- (mean(x)-50)/10 # Cohen-d kiszámítása
pwr.norm.test(d = d, n = 10, sig.level = 0.05, alternative="two.sided")##
## Mean power calculation for normal distribution with known variance
##
## d = 0.8
## n = 10
## sig.level = 0.05
## power = 0.7156166
## alternative = two.sidedAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 71,56%-os.
A mintaelemszám meghatározása az egymintás u-próbában. Ha 90%-os statisztikai erőre van szükségünk a próba végrehajtása során, akkor ugyanilyen minimális hatásnagyság kimutatásához (\(d=0,8\)), mekkora mintaelemszámra van szükség?
library(pwr)
pwr.norm.test(d = 0.8, power = 0.9, sig.level = 0.05, alternative="two.sided")##
## Mean power calculation for normal distribution with known variance
##
## d = 0.8
## n = 16.41786
## sig.level = 0.05
## power = 0.9
## alternative = two.sidedLátható, hogy a 90%-os statisztikai erő eléréséhez (kerekítve) 16 elemű minta szükséges.
Alternatívák az egymintás u-próba végrehajtására. Egymintás u-próba végrehajtásához a BSDA és a TeachingDemos csomag z.test() függvényét is használhatjuk.
library(BSDA)
BSDA::z.test(x = x, mu = 50, sigma.x = 10)##
## One-sample z-Test
##
## data: x
## z = 2.5298, p-value = 0.01141
## alternative hypothesis: true mean is not equal to 50
## 95 percent confidence interval:
## 51.80205 64.19795
## sample estimates:
## mean of x
## 58library(TeachingDemos)
TeachingDemos::z.test(x = x, mu = 50, stdev = 10)##
## One Sample z-test
##
## data: x
## z = 2.5298, n = 10.0000, Std. Dev. = 10.0000, Std. Dev. of the
## sample mean = 3.1623, p-value = 0.01141
## alternative hypothesis: true mean is not equal to 50
## 95 percent confidence interval:
## 51.80205 64.19795
## sample estimates:
## mean of x
## 583.1.2 Példa egyoldali (bal, kisebb) ellenhipotézisre: szorongáscsökkentő mellékhatása
Pszichiáterek új szorongás elleni gyógyszert tesztelnek, amelynek egy lehetséges mellékhatása a pulzusszám csökkenése lehet. Összesen 50 orvostanhallgatónál 6 hetes gyógyszerfogyasztás után megmérték a pulzusszámot, melynek átlaga 70 ütés per perc. Tudjuk, hogy populációban a pulzusszám normális eloszlású, várható érték 72, szórás 12. A pszichiáter levonhatja azt a következtetést, hogy az új gyógyszer csökkenti a pulzusszámot?
Forrás: (Cohen 2013, 162)
Amennyiben a gyógyszer csökkenti a pulzusszámot, akkor az új változó várható értéke kisebb lesz, mint a szokásos 72 ütés per perc. Feltételezzük, hogy az új változó populációbeli szórása marad 12, így bal oldali (kisebb) ellenhipotézissel hajtjuk végre az egymintás u-próbát. A null- és ellenhipotézisek:
- \(H_0: \mu = 72\)
- \(H_1: \mu < 72\)
Az egymintás u-próba végrehajtása egyoldali (bal, kisebb) ellenhipotézissel. A példában a minta helyett összesítő adatokat találunk, így a PASWR2 csomagból a zsum.test() függvényt használjuk az egymintás u-próba végrehajtására. Megadjuk a mintaátlagot (mean.x=), a mintaelemek számát (n.x=), az ismert szórást (sigma.x=) és a hipotetikus várható értéket (mu=), valamint nem felejtkezünk el az alternative = "less" argumentumról sem, amely biztosítja, hogy a próba bal oldali legyen.
library(PASWR2)
PASWR2::zsum.test(mean.x = 70, n.x = 50, sigma.x = 12, mu = 72, alternative = "less")##
## One Sample z-test
##
## data: User input summarized values for x
## z = -1.1785, p-value = 0.1193
## alternative hypothesis: true difference in means is less than 72
## 95 percent confidence interval:
## -Inf 72.79141
## sample estimates:
## mean of x
## 70Az egymintás u-próba értékelése egyoldali (bal, kisebb) ellenhipotézis esetén. Az egyoldali ellenhipotézissel végrehajtott egymintás u-próba eredménye alapján azt mondhatjuk, hogy nincs elegendő bizonyítékunk arra, hogy a szorongáscsökkentő gyógyszer csökkenti a pulzusszámot (\(z=-1,1785\); \(p = 0,1193\)).
Az egymintás u-próba kézi számolása egyoldali (bal, kisebb) ellenhipotézis esetén. A próba outputjában szereplő értékeket a fent megadott próbastatisztika alapján magunk is kiszámolhatjuk:
atlag <- 70 # mintaátlag
szoras <- 12 # populációbeli szórás
n <- 50 # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
mu.0 <- 72 # hipotetikus várható érték
z <- (atlag-mu.0)/SE # próbastatisztika értéke
z # próbastatisztika értékének kiírása## [1] -1.178511pnorm(q = z) # a p érték egyoldali (bal, kisebb) próba esetén## [1] 0.1192964Az egymintás u-próbához kapcsolódó konfidenciaintervallum egyoldali (bal, kisebb) ellenhipotézis esetén. A próba outputjában szereplő konfidenciaintervallum határait magunk is kiszámolhatjuk. Jelen egyoldali bal, kisebb ellenhipotézis (\(H_1: \mu < 72\)) esetében válik világossá a statisztikai próbák és a konfidenciaintervallumok közötti megközelítésbeli különbség. A statisztikai próba a nullhipotézis teljesülése felől közelít (vagyis a populáció hirtelen ismertté válik), és az adatok megfelelését vizsgálja ezen populációbeli eloszláshoz. Bal oldali esetben ez azt jelenti, hogy a kritikus tartomány a bal oldalon helyezkedik el, a megtartási tartomány pedig ettől jobbra található, és egészen a pozitív végtelenig tart. Ugyanis a nullhipotézis állításának a 72 vagy annál nagyobb átlagok teljesen megfelelnek, az ellenhipotézis szerint csak a 72-nél kisebb értékek a kritikusak. A konfidenciaintervallum készítése az adatokból indul ki, és azt vizsgálja, hogy a populációbeli hipotetikus érték megfelel-e ennek az intervallumnak (vagyis beleesik vagy sem). Bal oldali ellenhipotézis esetén az adatok alapján készített konfidenciaintervallum a mínusz végtelentől egy adott értékig tart, és az adatoknak megfelelő populációbeli várható értékeket tartalmazza. Ha a hipotetikus 72 érték beleesik ebbe az intervallumba, akkor a nullhipotézist támogatjuk, ha azonban ettől az intervallumtól jobbra helyezkedik el, akkor az ellenhipotézist, miszerint populációbeli várható érték kisebb a 72 hipotetikus értéknél.
Normális eloszlás és ismert \(\sigma\) szórás esetén a várható értékre vonatkozó bal oldali \(\left(1-\alpha \right)\) megbízhatóságú konfidenciaintervallum:
\[\left] - \infty , \bar{X}+u_{\alpha}\frac{\sigma}{\sqrt{n}} \right[\]
# A bal oldali 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- 70 # mintaátlag
szoras <- 12 # populációbeli szórás
n <- 50 # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
alfa <- 0.05 # alfa=1-0.95
u.alfa <- qnorm(p = 1-alfa) # u_alfa kritikusérték
atlag + c(-Inf, u.alfa*SE) # a bal odali 95%-os konf.intv. határai ## [1] -Inf 72.79141Az egymintás u-próbában a hatás nagyságának meghatározása egyoldali (bal, kisebb) ellenhipotézis esetén. Az egymintás u-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{\bar{X}-\mu_0}{\sigma}\right|\]
abs((70-72)/12) # Cohen-d kiszámítása## [1] 0.1666667A Cohen-d értéke 0,17, ami azt mutatja, hogy a hatás kis mértékű.
Az egymintás u-próbában az erő meghatározása egyoldali (bal, kisebb) ellenhipotézis esetén. A statisztikai erő meghatározásához a pwr csomag pwr.norm.test() függvényét használjuk. A bemenő paraméterek:
n=- a mintaelemszámd=- a hatás nagyságasig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formája
library(pwr)
d <- -0.1666666 # Cohen-d értéke, előjelesen
pwr.norm.test(d = d, n = 50, sig.level = 0.05, alternative="less")##
## Mean power calculation for normal distribution with known variance
##
## d = -0.1666666
## n = 50
## sig.level = 0.05
## power = 0.3204851
## alternative = lessAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 32%-os.
Mintaelemszám meghatározása az egymintás u-próbában egyoldali (bal, kisebb) ellenhipotézis esetén. Ha 80%-os statisztikai erőre van szükségünk a próba végrehajtása során, akkor ugyanilyen hatásnagyság kimutatásához (\(d=-0,167\)), mekkora mintaelemszámra van szükség?
d <- -0.1666666 # Cohen-d értéke, előjelesen
pwr.norm.test(d = d, power = 0.8, sig.level = 0.05, alternative="less")##
## Mean power calculation for normal distribution with known variance
##
## d = -0.1666666
## n = 222.5722
## sig.level = 0.05
## power = 0.8
## alternative = lessLátható, hogy a 80%-os statisztikai erő eléréséhez (kerekítve) 223 elemű minta szükséges.
3.1.3 Példa egyoldali (jobb, nagyobb) ellenhipotézisre: az elfojtott düh hatása
Egy elképzelt vizsgálatban annak a 64 tanulónak, akik nagyon magas pontszámot értek el egy a dühvel kapcsolatos kérdőíven, megmérték a szisztolés vérnyomását. Az átlag 124 Hgmm lett. A populációban a szisztolés vérnyomás normális eloszlású: \(N(120, 10)\). Következtethetünk arra, hogy az elfojtott düh kapcsolatban van a magas vérnyomással?
Forrás: (Cohen 2013, 162)
Az elfojtott düh vérnyomásnövelő hatását úgy tudnánk bizonyítani, ha a vizsgált populációban a szisztolés vérnyomás a szokásos 120 Hgmm-nél nagyobb lenne. Az egymintás u-próba feltételei teljesülnek, melyet most jobb oldali (nagyobb) ellenhipotézissel hajtjuk végre. A null- és ellenhipotézisek:
- \(H_0: \mu = 120\)
- \(H_1: \mu > 120\)
Az egymintás u-próba végrehajtása egyoldali (jobb, nagyobb) ellenhipotézissel. Ez a példa sem tartalmazza a mintát, így itt is a PASWR2 csomag zsum.test() függvényét használjuk. A jobb oldali ellenhipotézis miatt az alternative = "greater" argumentummal hívjuk a függvényt.
library(PASWR2)
PASWR2::zsum.test(mean.x = 124, n.x = 64, sigma.x = 10, mu = 120, alternative = "greater")##
## One Sample z-test
##
## data: User input summarized values for x
## z = 3.2, p-value = 0.0006871
## alternative hypothesis: true difference in means is greater than 120
## 95 percent confidence interval:
## 121.9439 Inf
## sample estimates:
## mean of x
## 124Az egymintás u-próba értékelése egyoldali (jobb, nagyobb) ellenhipotézis esetén. Az egyoldali ellenhipotézissel végrehajtott egymintás u-próba eredménye alapján azt mondhatjuk, hogy az elfojtott düh szignifikánsan megnöveli a szisztolés vérnyomás mértékét (\(z=3,2\); \(p = 0,0007\)).
Az egymintás u-próba kézi számolása egyoldali (jobb, nagyobb) ellenhipotézis esetén. A próba outputjában szereplő értékeket a fent megadott próbastatisztika alapján magunk is kiszámolhatjuk:
atlag <- 124 # mintaátlag
szoras <- 10 # populációbeli szórás
n <- 64 # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
mu.0 <- 120 # hipotetikus várható érték
z <- (atlag-mu.0)/SE # próbastatisztika értéke
z # próbastatisztika értékének kiírása## [1] 3.21-pnorm(q = z) # a p érték egyoldali (jobb, nagyobb) próba esetén## [1] 0.0006871379Az egymintás u-próbához kapcsolódó konfidenciaintervallum egyoldali (jobb, nagyobb) ellenhipotézis esetén. A próba outputjában szereplő konfidenciaintervallum határait magunk is kiszámolhatjuk. Jelen egyoldali jobb, nagyobb ellenhipotézis (\(H_1: \mu > 120\)) esetében szintén jól érzékelhető a statisztikai próbák és a konfidenciaintervallumok közötti megközelítésbeli különbség. A statisztikai próba a nullhipotézis teljesülése felől közelít (vagyis a populáció hirtelen ismertté válik), és az adatok megfelelését vizsgálja ezen populációbeli eloszláshoz. Jobb oldali esetben ez azt jelenti, hogy a kritikus tartomány a jobb oldalon helyezkedik el, a megtartási tartomány pedig ettől balra található, és egészen a negatív végtelenig tart. Ugyanis a nullhipotézis állításának a 120 vagy annál kisebb átlagok teljesen megfelelnek, az ellenhipotézis szerint csak a 120-nél nagyobb értékek a kritikusak. A konfidenciaintervallum készítése az adatokból indul ki, és azt vizsgálja, hogy a populációbeli hipotetikus érték megfelel-e ennek az intervallumnak (vagyis beleesik vagy sem). Jobb oldali ellenhipotézis esetén az adatok alapján készített konfidenciaintervallum a plusz végtelentől egy adott értékig tart, és az adatoknak megfelelő populációbeli várható értékeket tartalmazza. Ha a hipotetikus 120 érték beleesik ebbe az intervallumba, akkor a nullhipotézist támogatjuk, ha azonban ettől az intervallumtól balra helyezkedik el, akkor az ellenhipotézist, miszerint populációbeli várható érték nagyobb a 120 hipotetikus értéknél.
Normális eloszlás és ismert \(\sigma\) szórás esetén a várható értékre vonatkozó jobb oldali \(\left(1-\alpha \right)\) megbízhatóságú konfidenciaintervallum:
\[\left] \bar{X}-u_{\alpha}\frac{\sigma}{\sqrt{n}}, + \infty \right[\]
# A jobb oldali 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- 124 # mintaátlag
szoras <- 10 # populációbeli szórás
n <- 64 # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
alfa <- 0.05 # alfa=1-0.95
u.alfa <- qnorm(p = 1-alfa) # u_alfa kritikusérték
atlag + c(-u.alfa*SE, Inf) # a bal odali 95%-os konf.intv. határai ## [1] 121.9439 InfAz egymintás u-próbában a hatás nagyságának meghatározása egyoldali (jobb, nagyobb) ellenhipotézis esetén. Az egymintás u-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{\bar{X}-\mu_0}{\sigma}\right|\]
abs((124-120)/10) # Cohen-d kiszámítása## [1] 0.4A Cohen-d értéke 0.17, ami azt mutatja, hogy a hatás közepes mértékű.
Az egymintás u-próbában az erő meghatározása egyoldali (jobb, nagyobb) ellenhipotézis esetén. A statisztikai erő meghatározásához a pwr csomag pwr.norm.test() függvényét használjuk. A bemenő paraméterek:
n=- a mintaelemszámd=- a hatás nagyságasig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formája
library(pwr)
d <- 0.4 # Cohen-d értéke, előjelesen
pwr.norm.test(d = d, n = 64, sig.level = 0.05, alternative="greater")##
## Mean power calculation for normal distribution with known variance
##
## d = 0.4
## n = 64
## sig.level = 0.05
## power = 0.9400444
## alternative = greaterAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 94%-os.
Mintaelemszám meghatározása az egymintás u-próbában egyoldali (jobb, nagyobb) ellenhipotézis esetén. Ha 80%-os statisztikai erőre van szükségünk a próba végrehajtása során, akkor ugyanilyen hatásnagyság kimutatásához (\(d=0,4\)), mekkora mintaelemszámra van szükség?
d <- 0.4 # Cohen-d értéke, előjelesen
pwr.norm.test(d = d, power = 0.8, sig.level = 0.05, alternative="greater")##
## Mean power calculation for normal distribution with known variance
##
## d = 0.4
## n = 38.64099
## sig.level = 0.05
## power = 0.8
## alternative = greaterLátható, hogy a 80%-os statisztikai erő eléréséhez már egy (kerekítve) 39 elemű minta elegendő.
3.2 Páros u-próba
A páros u-próba két összetartozó minta esetén a különbségváltozó várható értékének (\(\mu_d=\mu_1-\mu_2\)) adott értéktől (\(d_0\)) való eltérését vizsgálja, miközben a különbségváltozó populációbeli szórása ismert.
Alkalmazási feltételek:
- véletlen, összetartozó (páros) minta: \((X_1, X_2)\)
- az \(X_1\) és \(X_2\) normális eloszlású (elegendő, ha a \(X_1-X_2\) különbségváltozó normális eloszlású)
- ismert \(\sigma_d\) populációbeli szórás a \(X_1-X_2\) különbségváltozóra
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu_d=d_0\)
- ha \(d_0=0\), akkor \(H_0: \mu_1-\mu_2=0\) vagy \(H_0: \mu_1=\mu_2\) formában is írható
- Ellenhipotézis:
- \(H_1: \mu_d \neq d_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_d < d_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_d > d_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
- ha \(d_0=0\), akkor a fenti ellenhipotézisek:
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_1<\mu_2\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_1>\mu_2\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
\[Z=\frac{(\bar{X_1}-\bar{X_2})-d_0}{\sigma_d/\sqrt{n}} \sim N(0,1)\]
3.2.1 Példa: intelligencia pontszám változása.
Tréning előtt (IQ1 változó) és tréning után (IQ2 változó) intelligencia tesztet töltettünk ki 20 személlyel. A változás szokásos mértéke IQ1-IQ2 = -10. Vizsgáljuk meg, hogy a mintánk megfelel-e a várakozásnak? Az intelligencia teszten elért pontok különbségének populációbeli szórása \(\sigma_d=1,4\).
Forrás: (Taeger and Kuhnt 2014)
A feladatban a két időpontban mért IQ változó várható értékének különbségét vizsgáljuk. A páros t-próba null- és ellenhipotézise:
- \(H_0: \mu_1-\mu_2=-10\)
- \(H_1: \mu_1-\mu_2 \neq -10\)
Adatok beolvasása. Első lépésben beolvassuk az adatokat egy d adattáblába. Az adattábla tartalmazza a személyek azonosítóját (no változó), és a két időpontban mért intelligencia pontszámot (IQ1 és IQ2).
d <- read.table(file = textConnection("
no,IQ1,IQ2
1,127,137
2,98,108
3,105,115
4,83,93
5,133,143
6,90,100
7,107,117
8,98,108
9,91,101
10,100,110
11,88,98
12,96,106
13,110,120
14,87,97
15,88,98
16,88,100
17,105,115
18,95,111
19,79,89
20,106,116
"), header=T, sep=",")
d$no <- factor(d$no) # a személyek sorszámát faktorrá alakítjuk
str(d) # az adattábla szerkezete## 'data.frame': 20 obs. of 3 variables:
## $ no : Factor w/ 20 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## $ IQ1: int 127 98 105 83 133 90 107 98 91 100 ...
## $ IQ2: int 137 108 115 93 143 100 117 108 101 110 ...d # a beolvasott adattábla## no IQ1 IQ2
## 1 1 127 137
## 2 2 98 108
## 3 3 105 115
## 4 4 83 93
## 5 5 133 143
## 6 6 90 100
## 7 7 107 117
## 8 8 98 108
## 9 9 91 101
## 10 10 100 110
## 11 11 88 98
## 12 12 96 106
## 13 13 110 120
## 14 14 87 97
## 15 15 88 98
## 16 16 88 100
## 17 17 105 115
## 18 18 95 111
## 19 19 79 89
## 20 20 106 116A páros adatok vizsgálatához is előkészítjük adatainkat. A PairedData csomag paired() függvényét használjuk az átalakításhoz. A későbbiekben a d és d.paired adattáblákat is használni fogjuk.
library(PairedData)
d.paired <- with(d, paired(IQ1, IQ2)) # adatelőkészítés a PairedData csomag használatához
d.paired # a páros minta## Object of class "paired"
## IQ1 IQ2
## 1 127 137
## 2 98 108
## 3 105 115
## 4 83 93
## 5 133 143
## 6 90 100
## 7 107 117
## 8 98 108
## 9 91 101
## 10 100 110
## 11 88 98
## 12 96 106
## 13 110 120
## 14 87 97
## 15 88 98
## 16 88 100
## 17 105 115
## 18 95 111
## 19 79 89
## 20 106 116A páros u-próba végrehajtása. A páros u-próba végrehajtásához a PASWR2 csomag z.test() függvényét használjuk. Megadjuk a páros mintát az x= és y= argumentumokban, továbbá a különbségváltozó populációbeli szórását (sigma.d=), a hipotetikus különbséget (mu=) és a próba összetartozó jellegét biztosító paired=T argumentumot.
library(PASWR2)
PASWR2::z.test(x = d$IQ1, y = d$IQ2, sigma.d = 1.4, mu = -10, paired = T)##
## Paired z-test
##
## data: d$IQ1 and d$IQ2
## z = -1.2778, p-value = 0.2013
## alternative hypothesis: true difference in means is not equal to -10
## 95 percent confidence interval:
## -11.013566 -9.786434
## sample estimates:
## mean of the differences
## -10.4A páros u-próba értékelése. A páros u-próba eredménye alapján azt mondhatjuk, hogy nincs elegendő bizonyítékunk, hogy az IQ szokásos 10 pontos növekedését megcáfoljuk (\(z=-1,2778\); \(p = 0,2013\)).
A páros u-próba kézi számolása. A próba outputjában szereplő értékeket magunk is kiszámolhatjuk:
atlag <- mean(d$IQ1 - d$IQ2, na.rm = T) # a különbségváltozó mintaátlaga
szoras <- 1.4 # populációbeli szórás
n <- sum(!is.na(d$IQ1)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
d.0 <- -10 # a különbségváltozó hipotetikus várható értéke
z <- (atlag-d.0)/SE # próbastatisztika értéke
z # próbastatisztika értékének kiírása## [1] -1.2777532*(1-pnorm(q = abs(z))) # a p érték kétoldali próba esetén## [1] 0.2013365Konfidenciaintervallum kézi számolása páros u-próba esetén. Az \(\left( 1-\alpha \right)\) konfidenciaintervallum kiszámítása nem tér el az egymintás esettől, csak most a különbségváltozóval kell számolnunk.
\[\left] (\bar{X_1}-\bar{X_2})-u_{\alpha}\frac{\sigma_d}{\sqrt{n}}, (\bar{X_1}-\bar{X_2})+u_{\alpha}\frac{\sigma_d}{\sqrt{n}} \right[\]
# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- mean(d$IQ1-d$IQ2, na.rm = T) # a különbségváltozó mintaátlaga
szoras <- 1.4 # populációbeli szórás
n <- sum(!is.na(d$IQ1)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
alfa <- 0.05 # alfa=1-0.95
u.alfa <- qnorm(p = 1-alfa/2) # u_alfa kritikusérték
atlag + c(-u.alfa*SE, u.alfa*SE) # a 95%-os konf.intv. határai ## [1] -11.013566 -9.786434Alkalmazási feltételek ellenőrzése páros u-próbához. A páros u-próba feltételeinek ellenőrzése történhet Shapiro-Wilk próbával:
shapiro.test(d$IQ1) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: d$IQ1
## W = 0.91329, p-value = 0.07364shapiro.test(d$IQ2) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: d$IQ2
## W = 0.92045, p-value = 0.1011shapiro.test(d$IQ1-d$IQ2) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: d$IQ1 - d$IQ2
## W = 0.32979, p-value = 0.0000000127A fenti outputokból kiolvasható, hogy IQ1 és IQ2 normalitását nem tudjuk megcáfolni, a különbségváltozó azonban nem normális eloszlású.
Leíró statisztikai vizsgálatok a páros u-próbához. A PairedData csomag summary() függvénye az előkészített d.paired adattábla esetén a páros mintáknál megszokott mutatókat jeleníti meg. Mutatókat kapunk a két összetartozó mintára, azok különbségére és átlagára is.
library(PairedData)
PairedData::summary(d.paired) # mutatók a páros mintára ## $stat
## n mean median trim sd IQR (*) median ad (*)
## IQ1 (x) 20 98.7 97 96.66667 13.727038 12.78725 13.3434
## IQ2 (y) 20 109.1 108 107.33333 13.630075 11.67532 11.8608
## x-y 20 -10.4 -10 -10.00000 1.391705 0.00000 0.0000
## (x+y)/2 20 103.9 103 102.00000 13.660932 12.23128 12.6021
## mean ad (*) sd(w) min max
## IQ1 (x) 12.7838042 11.95591 79 133
## IQ2 (y) 12.6584728 11.84861 89 143
## x-y 0.5013257 0.00000 -16 -10
## (x+y)/2 12.5331414 11.85292 84 138
##
## $cor
## cor wcor
## (x,y) 0.9948492 0.9834514Grafikus lehetőséges páros u-próbára. A PairedData csomag az előkészített d.paired adattáblára grafikus megjelenítést is lehetővé tesz. Rajzolhatunk kétdimenziós pontdiagramot, valamint dobozdiagramot a párosított mintaelemek megjelenítésével is.
library(gridExtra)
library(PairedData)
p1 <- plot(d.paired) + theme_bw() # kétdimenziós pontdiagram
p2 <- plot(d.paired, type="profile") + theme_bw() # dobozdiagram és a páros mintaelemek
grid.arrange(p1, p2, ncol = 2) # ábrák megjelenítése
A páros u-próbában a hatás nagyságának meghatározása. Páros u-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{(\bar{X_1}-\bar{X_2})-d_0}{\sigma}\right|\]
(mean(d$IQ1-d$IQ2, na.rm = T) - -10)/1.4 # Cohen-d kiszámítása## [1] -0.2857143A Cohen-d értéke 0,29, ami azt mutatja, hogy a hatás kis-közepes mértékű.
A páros u-próbában az erő meghatározása. A statisztikai erő meghatározásához a pwr csomag pwr.norm.test() függvényét használjuk. A bemenő paraméterek:
n=- a mintaelemszámd=- a hatás nagyságasig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formája
library(pwr)
pwr.norm.test(d = 0.29, n = 20, sig.level = 0.05, alternative="two.sided")##
## Mean power calculation for normal distribution with known variance
##
## d = 0.29
## n = 20
## sig.level = 0.05
## power = 0.2542142
## alternative = two.sidedAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 25%-os.
Mintaelemszám meghatározása a páros u-próbában. Ha 80%-os statisztikai erőre van szükségünk a próba végrehajtása során, akkor ugyanilyen hatásnagyság kimutatásához (\(d=0,29\)), mekkora mintaelemszámra van szükség?
library(pwr)
pwr.norm.test(d = 0.29, power = 0.8, sig.level = 0.05, alternative="two.sided")##
## Mean power calculation for normal distribution with known variance
##
## d = 0.29
## n = 93.32771
## sig.level = 0.05
## power = 0.8
## alternative = two.sidedLátható, hogy a 80%-os statisztikai erő eléréséhez (kerekítve) 93 elemű minta szükséges.
3.3 Kétmintás u-próba
Azt teszteljük, hogy két független változó várható értékének különbsége (\(\mu_d=\mu_1-\mu_2\)) eltér-e egy adott értéktől (\(d_0\)). A változók normális eloszlásúak és \(\sigma_1\), \(\sigma_2\) szórásuk ismert.
Alkalmazási feltételek:
- két véletlen független minta: \(X_1\) és \(X_2\)
- \(X_1\) és \(X_2\) normális eloszlású a populációban
- ismert \(\sigma_1\) és \(\sigma_2\) populációbeli szórás az \(X_1\) és \(X_2\) változókra
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu_d=d_0\)
- ha \(d_0=0\), akkor \(H_0: \mu_1-\mu_2=0\) vagy \(H_0: \mu_1=\mu_2\) formában is írható
- Ellenhipotézis:
- \(H_1: \mu_d \neq d_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_d < d_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_d > d_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
- ha \(d_0=0\), akkor a fenti ellenhipotézisek:
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_1<\mu_2\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_1>\mu_2\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
\[Z=\frac{(\bar{X_1}-\bar{X_2})-d_0}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0,1)\]
3.3.1 Példa: magas vérnyomás
Azt vizsgáljuk, hogy egészségesek és magas vérnyomásban szenvedők körében eltér-e a szisztolés vérnyomás. Az egészséges csoportban (status=0), a populációbeli szórás \(\sigma_1=10\), a mintaelemszám \(n_1=25\), míg a betegek körében (status=1) \(\sigma_2=12\) és \(n_2=30\).
Forrás: (Taeger and Kuhnt 2014)
A normális eloszlás és az ismert szórások lehetővé teszik, hogy a két populációban vizsgált szisztolés vérnyomás változó várható értékének egyformaságát kétmintás u-próba segítségével vizsgálhassuk:
- \(H_0: \mu_1=\mu_2\)
- \(H_1: \mu_1 \neq \mu_2\)
Adatok beolvasása. Végezzük el az adatok beolvasását a d adattáblába. A no és status numerikus oszlopokat faktorrá alakítjuk.
d <- read.table(file = textConnection("
no,status,mmhg
1,0,120
2,0,115
3,0,94
4,0,118
5,0,111
6,0,102
7,0,102
8,0,131
9,0,104
10,0,107
11,0,115
12,0,139
13,0,115
14,0,113
15,0,114
16,0,105
17,0,115
18,0,134
19,0,109
20,0,109
21,0,93
22,0,118
23,0,109
24,0,106
25,0,125
26,1,150
27,1,142
28,1,119
29,1,127
30,1,141
31,1,149
32,1,144
33,1,142
34,1,149
35,1,161
36,1,143
37,1,140
38,1,148
39,1,149
40,1,141
41,1,146
42,1,159
43,1,152
44,1,135
45,1,134
46,1,161
47,1,130
48,1,125
49,1,141
50,1,148
51,1,153
52,1,145
53,1,137
54,1,147
55,1,169
"), header=T, sep=",")
d$no <- factor(d$no) # a személyek sorszámát faktorrá alakítjuk
d$status <- factor(d$status, labels=c("egészséges", "magas vérnyomás"))# a status faktorrá alakítása
str(d) # az adattábla szerkezete## 'data.frame': 55 obs. of 3 variables:
## $ no : Factor w/ 55 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## $ status: Factor w/ 2 levels "egészséges","magas vérnyomás": 1 1 1 1 1 1 1 1 1 1 ...
## $ mmhg : int 120 115 94 118 111 102 102 131 104 107 ...d # a beolvasott adattábla## no status mmhg
## 1 1 egészséges 120
## 2 2 egészséges 115
## 3 3 egészséges 94
## 4 4 egészséges 118
## 5 5 egészséges 111
## 6 6 egészséges 102
## 7 7 egészséges 102
## 8 8 egészséges 131
## 9 9 egészséges 104
## 10 10 egészséges 107
## 11 11 egészséges 115
## 12 12 egészséges 139
## 13 13 egészséges 115
## 14 14 egészséges 113
## 15 15 egészséges 114
## 16 16 egészséges 105
## 17 17 egészséges 115
## 18 18 egészséges 134
## 19 19 egészséges 109
## 20 20 egészséges 109
## 21 21 egészséges 93
## 22 22 egészséges 118
## 23 23 egészséges 109
## 24 24 egészséges 106
## 25 25 egészséges 125
## 26 26 magas vérnyomás 150
## 27 27 magas vérnyomás 142
## 28 28 magas vérnyomás 119
## 29 29 magas vérnyomás 127
## 30 30 magas vérnyomás 141
## 31 31 magas vérnyomás 149
## 32 32 magas vérnyomás 144
## 33 33 magas vérnyomás 142
## 34 34 magas vérnyomás 149
## 35 35 magas vérnyomás 161
## 36 36 magas vérnyomás 143
## 37 37 magas vérnyomás 140
## 38 38 magas vérnyomás 148
## 39 39 magas vérnyomás 149
## 40 40 magas vérnyomás 141
## 41 41 magas vérnyomás 146
## 42 42 magas vérnyomás 159
## 43 43 magas vérnyomás 152
## 44 44 magas vérnyomás 135
## 45 45 magas vérnyomás 134
## 46 46 magas vérnyomás 161
## 47 47 magas vérnyomás 130
## 48 48 magas vérnyomás 125
## 49 49 magas vérnyomás 141
## 50 50 magas vérnyomás 148
## 51 51 magas vérnyomás 153
## 52 52 magas vérnyomás 145
## 53 53 magas vérnyomás 137
## 54 54 magas vérnyomás 147
## 55 55 magas vérnyomás 169A kétmintás u-próba végrehajtása. A kétmintás u-próba végrehajtását a PASWR2 csomag z.test() függvényével kezdeményezzük. Megadjuk mindkét független mintát az x= és y= argumentumokban, majd a minták mögötti populáció ismert szórásait közöljük (sigma.x= és sigma.y).
library(PASWR2)
PASWR2::z.test(x = d$mmhg[ d$status %in% "egészséges"],
y = d$mmhg[ d$status %in% "magas vérnyomás"], sigma.x = 10, sigma.y = 12)##
## Two Sample z-test
##
## data: d$mmhg[d$status %in% "egészséges"] and d$mmhg[d$status %in% "magas vérnyomás"]
## z = -10.556, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -37.12753 -25.49914
## sample estimates:
## mean of x mean of y
## 112.9200 144.2333A kétmintás u-próba értékelése. A kétmintás u-próba eredménye alapján azt mondhatjuk, hogy elegendő bizonyítékunk van arra, hogy a szisztolés vérnyomás szignifikánsan eltér az egészségesek és magas vérnyomásban szenvedők két csoportjában. (\(z=-10,556\); \(p < 0,0001\)).
A kétmintás u-próba kézi számolása. A próba outputjában szereplő értékeket magunk is kiszámolhatjuk:
x.1 <- d$mmhg[ d$status %in% "egészséges"] # 1. adatminta
x.2 <- d$mmhg[ d$status %in% "magas vérnyomás"] # 2. adatminta
atlag <- mean(x.1, na.rm = T) - mean(x.2, na.rm = T) # mintaátlagok különbsége
szoras.1 <- 10 # 1. populációbeli szórás
szoras.2 <- 12 # 2. populációbeli szórás
n.1 <- sum(!is.na(x.1)) # 1. minta elemszáma
n.2 <- sum(!is.na(x.2)) # 2. minta elemszáma
SE <- sqrt(szoras.1^2/n.1 + szoras.2^2/n.2) # közös standard hiba
d.0 <- 0 # a különbségváltozó hipotetikus várható értéke
z <- (atlag-d.0)/SE # próbastatisztika értéke
z # próbastatisztika értékének kiírása## [1] -10.555722*(1-pnorm(q = abs(z))) # a p érték kétoldali próba esetén## [1] 0Konfidenciaintervallum kézi számolása kétmintás u-próbához. A próba outputjában szereplő konfidenciaintervallum határait kézi számolással is meghatározzuk. Az \(\left( 1-\alpha \right)\) konfidenciaintervallum kiszámítása:
\[\left] (\bar{X_1}-\bar{X_2})-u_{\alpha}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}, (\bar{X_1}-\bar{X_2})+u_{\alpha}\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} \right[\]
# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
x.1 <- d$mmhg[ d$status %in% "egészséges"] # 1. adatminta
x.2 <- d$mmhg[ d$status %in% "magas vérnyomás"] # 2. adatminta
atlag <- mean(x.1, na.rm = T) - mean(x.2, na.rm = T) # mintaátlagok különbsége
szoras.1 <- 10 # 1. populációbeli szórás
szoras.2 <- 12 # 2. populációbeli szórás
n.1 <- sum(!is.na(x.1)) # 1. minta elemszáma
n.2 <- sum(!is.na(x.2)) # 2. minta elemszáma
SE <- sqrt(szoras.1^2/n.1 + szoras.2^2/n.2) # közös standard hiba
alfa <- 0.05 # alfa=1-0.95
atlag + c(-u.alfa*SE, u.alfa*SE) # a 95%-os konf.intv. határai ## [1] -37.12753 -25.49914Alkalmazási feltételek ellenőrzése kétmintás u-próbához. A kétmintás u-próba feltételeinek ellenőrzését a Shapiro-Wilk próbával is elvégezhetjük.
by(d$mmhg, d$status, shapiro.test) # normalitás ellenőrzése Shapiro-Wilk-próbával## d$status: egészséges
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96052, p-value = 0.4249
##
## --------------------------------------------------------
## d$status: magas vérnyomás
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97971, p-value = 0.8179A fenti ouputból kiolvasható, hogy a két csoportra vonatkozó normalitási feltételt nem tudjuk megcáfolni.
Leíró statisztikai mutatók kétmintás u-próbához. A kétmintás u-próbához kapcsolódó leíró statisztikai vizsgálatok:
library(psych)
describeBy(x = d$mmhg, group = d$status)## group: egészséges
## vars n mean sd median trimmed mad min max range skew kurtosis se
## 1 1 25 112.92 11.15 113 112.52 8.9 93 139 46 0.47 -0.1 2.23
## --------------------------------------------------------
## group: magas vérnyomás
## vars n mean sd median trimmed mad min max range skew kurtosis se
## 1 1 30 144.23 10.96 144.5 144.38 6.67 119 169 50 -0.1 -0.02 2library(DescTools)
Desc(mmhg~status, data=d)## -------------------------------------------------------------------------
## mmhg ~ status
##
## Summary:
## n pairs: 55, valid: 55 (100.0%), missings: 0 (0.0%), groups: 2
##
##
## egészséges magas vérnyomás
## mean 112.9200000 144.2333333
## median 113.0000000 144.5000000
## sd 11.1539231 10.9566020
## IQR 12.0000000 8.7500000
## n 25 30
## np 45.4545455% 54.5454545%
## NAs 0 0
## 0s 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 36.452, df = 1, p-value = 0.000000001565library(pastecs)
print(by(d$mmhg, d$status, stat.desc, norm = T), digits = 2)## d$status: egészséges
## nbr.val nbr.null nbr.na min max
## 25.000 0.000 0.000 93.000 139.000
## range sum median mean SE.mean
## 46.000 2823.000 113.000 112.920 2.231
## CI.mean.0.95 var std.dev coef.var skewness
## 4.604 124.410 11.154 0.099 0.468
## skew.2SE kurtosis kurt.2SE normtest.W normtest.p
## 0.504 -0.104 -0.058 0.961 0.425
## --------------------------------------------------------
## d$status: magas vérnyomás
## nbr.val nbr.null nbr.na min max
## 30.000 0.000 0.000 119.000 169.000
## range sum median mean SE.mean
## 50.000 4327.000 144.500 144.233 2.000
## CI.mean.0.95 var std.dev coef.var skewness
## 4.091 120.047 10.957 0.076 -0.101
## skew.2SE kurtosis kurt.2SE normtest.W normtest.p
## -0.118 -0.022 -0.013 0.980 0.818A hatás nagyságának meghatározása kétmintás u-próbában. A kétmintás u-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{(\bar{X_1}-\bar{X_2})-\mu_0}{\sqrt{(\sigma_1^2+\sigma_2^2)/2}}\right|\]
x.1 <- d$mmhg[ d$status %in% "egészséges"] # 1. adatminta
x.2 <- d$mmhg[ d$status %in% "magas vérnyomás"] # 2. adatminta
atlag <- mean(x.1, na.rm = T) - mean(x.2, na.rm = T) # mintaátlagok különbsége
szoras.1 <- 10 # 1. populációbeli szórás
szoras.2 <- 12 # 2. populációbeli szórás
s <- sqrt((szoras.1^2 + szoras.2^2)/2) # közös szórás
atlag / s # a Cohen-d értéke, előjelesen## [1] -2.834976A Cohen-d értéke 2,83 ami azt mutatja, hogy a hatás nagy mértékű.
Alternatívák a kétmintás u-próba végrehajtására. Kétmintás u-próba végrehajtásához a BSDA csomag z.test() függvényét is használhatjuk.
library(BSDA)
BSDA::z.test(x = d$mmhg[ d$status %in% "egészséges"],
y = d$mmhg[ d$status %in% "magas vérnyomás"], sigma.x = 10, sigma.y = 12)##
## Two-sample z-Test
##
## data: d$mmhg[d$status %in% "egészséges"] and d$mmhg[d$status %in% "magas vérnyomás"]
## z = -10.556, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -37.12753 -25.49914
## sample estimates:
## mean of x mean of y
## 112.9200 144.23333.4 Egymintás t-próba
Az egymintás t-próba egy ismeretlen szórású normális eloszlású változó várható értékére vonatkozó hipotézist teszteli: a \(\mu\) várható érték eltér-e egy előre definiált \(\mu_0\) értéktől.
Alkalmazási feltételek:
- a minta változója a populációban normális eloszlású
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu=\mu_0\)
- Ellenhipotézis:
- \(H_1: \mu \neq \mu_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu < \mu_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu > \mu_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
A nullhipotézis igaz volta mellett a \(t\) próbastatisztika \(\left( n-1 \right)\) szabadsági fokú t eloszlású.
\[T=\frac{\bar{X}-\mu_0}{s / \sqrt{n}} \sim t(n-1)\]
3.4.1 Példa: a holdillúzió
A holdillúzió egy olyan optikai csalódás, mely során a horizonton lévő Holdat nagyobbnak látjuk, mint amikor magasan az égbolton van. Kaufman és Rock (1962) a holdillúzió létezését vizsgálta, amikor 10 vizsgálati személynek meg kellett becsülni, hogy a horizonton lévő Hold átmérője, hányszorosa a “normál” Hold átmérőjének. Az adatok a következők: 1,73 1,06 2,03 1,40 0,95 1,13 1,41 1,73 1,63 1,56. Létezik a holdillúzió jelensége?
Forrás: (Howell 2013, 191)
A holdillúzió jelenség létezéséhez azt kell bizonyítanunk, hogy a horizonton lévő Hold képzelt átmérője nem 1-szerese a valóságos átmérőnek. Egymintás t-próbát a következő null-és ellenhipotézissel hajtjuk végre:
- \(H_0: \mu = 1\)
- \(H_1: \mu \neq 1\)
Adatok beolvasása. Első lépésként hozzuk létre x adatvektorban a mintát:
# adatvektor létrehozása
x <- c(1.73, 1.06, 2.03, 1.40, 0.95, 1.13, 1.41, 1.73, 1.63, 1.56)Egymintás t-próba végrehajtása. Egymintás t-próba végrehajtásához a t.test() függvényt használjuk. Megadjuk az adatmintát az x= argumentumban, majd a hipotetikus várható értéket a mu= argumentumban.
t.test(x = x, mu = 1)##
## One Sample t-test
##
## data: x
## t = 4.2976, df = 9, p-value = 0.001998
## alternative hypothesis: true mean is not equal to 1
## 95 percent confidence interval:
## 1.219287 1.706713
## sample estimates:
## mean of x
## 1.463Az egymintás t-próba értékelése. Az egymintás t-próba eredményéből kiolvasható, hogy a holdillúzió jelensége létezik, vagyis a horizonton lévő Hold képzelt átmérője a valós átmérő 1-szeresénél szignifikánsan nagyobb (\(t(9)=4,2976; p=0,002\)).
Az egymintás t-próba kézi számolása. A próba outputjában szereplő értékeket a fent megadott próbastatisztika alapján magunk is kiszámolhatjuk:
atlag <- mean(x, na.rm = T) # mintaátlag
szoras <- sd(x, na.rm = T) # minta szórása
n <- sum(!is.na(x)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
mu.0 <- 1 # hipotetikus várható érték
t <- (atlag-mu.0)/SE # próbastatisztika értéke
t # próbastatisztika értékének kiírása## [1] 4.2975922*(1-pt(q = abs(t), df = n-1)) # a p érték kétoldali próba esetén## [1] 0.001997695Az egymintás t-próbához kapcsolódó konfidenciaintervallum. A próba outputjában szereplő konfidenciaintervallum határait a DescTools csomag MeanCI() függvényével is meghatározhatjuk, de a kézi kiszámolása sem túl bonyolult. A várható értékre vonatkozó \(\left(1-\alpha \right)\) megbízhatóságú konfidenciaintervallum:
\[\left] \bar{X}-t_{\alpha, df}\frac{s}{\sqrt{n}}, \bar{X}+t_{\alpha, df}\frac{s}{\sqrt{n}} \right[\]
A MeanCI() függvény argumentumában meg kell adnunk az adatmintát (x=), valamint opcionálisan a megbízhatósági szintet (conf.level=) és a hiányzó értékek eltávolítására használatos na.rm=T paramétert.
library(DescTools)
MeanCI(x = x, conf.level = 0.95, na.rm=T) # 95%-os konfidenciaintervallum## mean lwr.ci upr.ci
## 1.463000 1.219287 1.706713# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- mean(x, na.rm = T) # mintaátlag
szoras <- sd(x, na.rm = T) # minta szórása
n <- sum(!is.na(x)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
alfa <- 0.05 # alfa=1-0.95
t.alfa <- qt(p = 1-alfa/2, df = n-1) # t_{alfa,df} kritikusérték
atlag + c(-t.alfa*SE, t.alfa*SE) # a 95%-os konf.intv. határai ## [1] 1.219287 1.706713Az alkalmazási feltételek ellenőrzése az egymintás t-próbához. Az egymintás t-próba alkalmazási feltétele, hogy a vizsgált szorongás változó normális eloszlású legyen a populációban. Ezt a shapiro.test() függvénnyel tesztelhetjük, illetve végezhetünk grafikus vizsgálatot, például rajzolhatunk hisztogramot, simított hisztogramot és QQ-ábrát.
shapiro.test(x) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.96283, p-value = 0.8176library(ggplot2) # a ggplot2 grafikát tartalmazó csomag
library(gridExtra) # több ábrát egy képen jeleníthetünk meg ezzel a csomaggal
p1 <- ggplot(data = data.frame(x), aes(x = x)) + # normalitás ellenőrzése hisztogrammal
geom_histogram(binwidth = .2, right=T, col="#00ADEE", fill="#C7EBFC", size=1) + theme_bw()
p2 <- ggplot(data = data.frame(x), aes(x = x)) + geom_density() # normalitás ellenőrzése simított hisztogrammal
p3 <- ggplot(data = data.frame(x), aes(sample = x)) + stat_qq() # normalitás ellenőrzése QQ-ábrával
grid.arrange(p1, p2, p3, ncol=3) # ábrák megjelenítése## Warning: `right` is deprecated. Please use `closed` instead.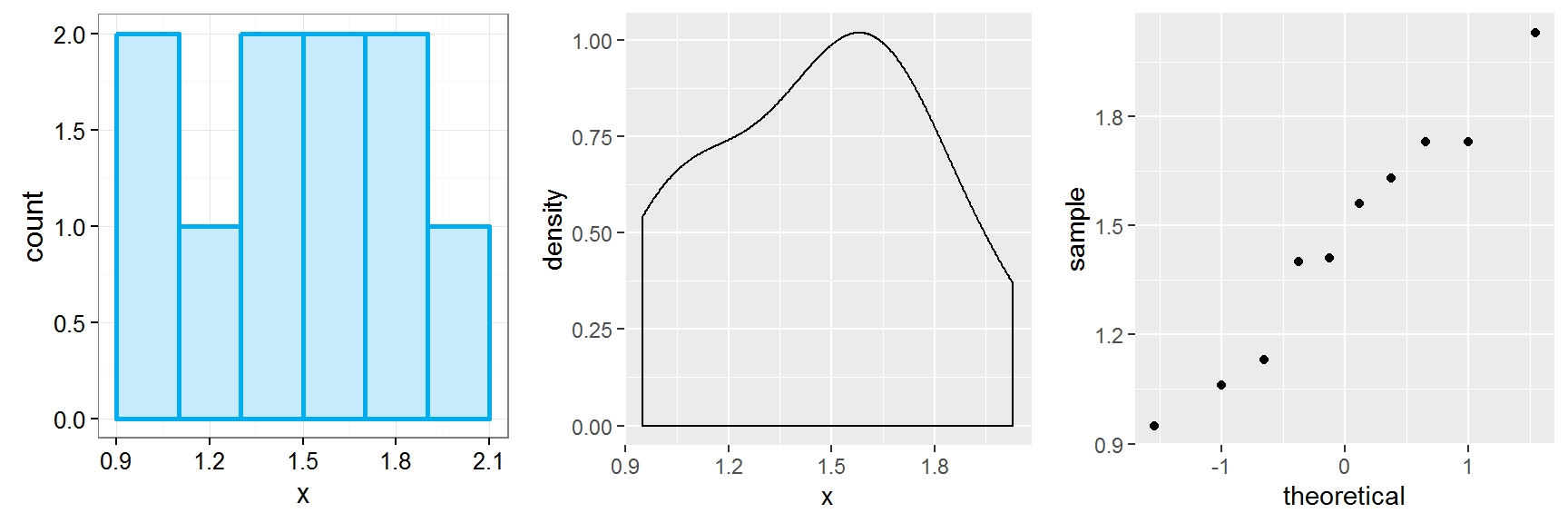
A Shapiro-Wilk próba eredménye nem cáfolja a változó normalitását (\(p=0,8176\)), és ugyanilyen következtetést vonhatunk le az ábrákról is.
Leíró statisztikák az egymintás t-próbához. Egyetlen változó esetén nagyon egyszerűen határozzuk meg a leíró statisztikai mutatókat. Az alapértelmezett summary() mellett számos csomagban találunk függvény a mutatók kiírására. Most a psych csomag describe(), a DescTools csomag Desc() és pastecs csomag stat.desc() függvényére mutatunk példát:
summary(x) # mutatók a beépített summary() függvényével## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.950 1.197 1.485 1.463 1.705 2.030library(psych)
psych::describe(x = x) # mutatók a psych csomag describe() függvényével## vars n mean sd median trimmed mad min max range skew kurtosis
## 1 1 10 1.46 0.34 1.48 1.46 0.36 0.95 2.03 1.08 -0.03 -1.35
## se
## 1 0.11library(DescTools)
Desc(x = x) # mutatók a DescTools csomag Desc() függvényével## -------------------------------------------------------------------------
## x (numeric)
##
## length n NAs unique 0s mean meanSE
## 10 10 0 9 0 1.4630 0.1077
##
## .05 .10 .25 median .75 .90 .95
## 0.9995 1.0490 1.1975 1.4850 1.7050 1.7600 1.8950
##
## range sd vcoef mad IQR skew kurt
## 1.0800 0.3407 0.2329 0.3632 0.5075 -0.0300 -1.3496
##
##
## level freq perc cumfreq cumperc
## 1 0.95 1 10.0% 1 10.0%
## 2 1.06 1 10.0% 2 20.0%
## 3 1.13 1 10.0% 3 30.0%
## 4 1.4 1 10.0% 4 40.0%
## 5 1.41 1 10.0% 5 50.0%
## 6 1.56 1 10.0% 6 60.0%
## 7 1.63 1 10.0% 7 70.0%
## 8 1.73 2 20.0% 9 90.0%
## 9 2.03 1 10.0% 10 100.0%library(pastecs)
print(stat.desc(x = x, norm=T), digits = 2) # mutatók a pastecs csomag stat.desc() függvényével## nbr.val nbr.null nbr.na min max
## 10.000 0.000 0.000 0.950 2.030
## range sum median mean SE.mean
## 1.080 14.630 1.485 1.463 0.108
## CI.mean.0.95 var std.dev coef.var skewness
## 0.244 0.116 0.341 0.233 -0.030
## skew.2SE kurtosis kurt.2SE normtest.W normtest.p
## -0.022 -1.350 -0.506 0.963 0.818Grafikus vizsgálat az egymintás t-próbához. A PASWR2 csomag eda() függvényével több leíró statisztikai ábrát is megrajzolhatunk.
library(PASWR2)
PASWR2::eda(x = x)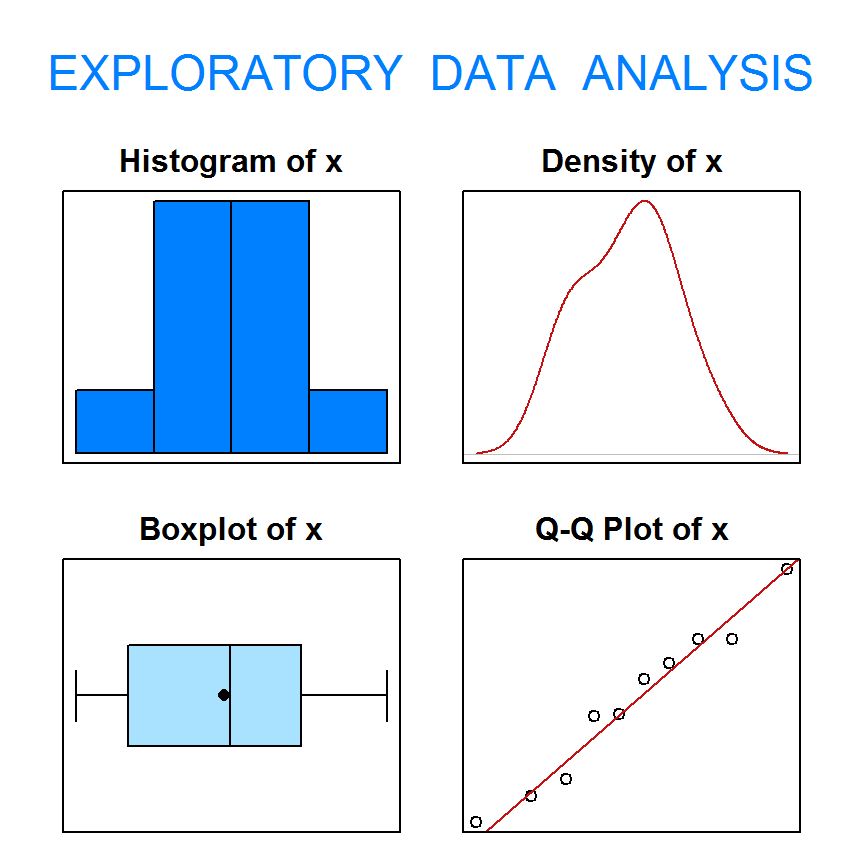
## Size (n) Missing Minimum 1st Qu Mean Median TrMean 3rd Qu
## 10.000 0.000 0.950 1.197 1.463 1.485 1.463 1.705
## Max Stdev Var SE Mean I.Q.R. Range Kurtosis Skewness
## 2.030 0.341 0.116 0.108 0.508 1.080 -1.350 -0.030
## SW p-val
## 0.818A hatás nagyságának meghatározása az egymintás t-próbához. A t-próbához tartozó hatásméret kiszámítása a következő összefüggéssel történik.
\[d=\left|\frac{\bar{X}-\mu_0}{s}\right|\]
A hatásmérték kiszámítása az lsr csomag cohensD() függvényével és kézzel is könnyen kiszámolható:
library(lsr)
cohensD(x = x, mu = 1) # Cohen-d meghatározása## [1] 1.359018(mean(x)-1)/sd(x) # Cohen-d kézi kiszámítása## [1] 1.359018A Cohen-d értéke 1,36, ami azt mutatja, hogy a hatás nagysága jelentős.
A statisztikai erő meghatározása az egymintás t-próbában.
A statisztikai erő meghatározásához a pwr csomag pwr.t.test() függvényét használjuk. A bemenő paraméterek:
n=- a mintaelemszámd=- a hatás nagyságasig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formájatype=- a t próba típusa
library(pwr)
pwr.t.test(n = 10, d = 1.359, sig.level = 0.05, alternative = "two.sided", type = "one.sample")##
## One-sample t test power calculation
##
## n = 10
## d = 1.359
## sig.level = 0.05
## power = 0.9675853
## alternative = two.sidedAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 96,8%-os.
Mintaelemszám meghatározása egymintás t-próbához.
Ha 90%-os statisztikai erő elegendő, akkor ugyanilyen hatásnagyság kimutatásához (\(d=1,359\)), mekkora mintaelemszámra van szükség?
library(pwr)
pwr.t.test(power = 0.9, d = 1.359, sig.level = 0.05, alternative = "two.sided", type = "one.sample")##
## One-sample t test power calculation
##
## n = 7.857303
## d = 1.359
## sig.level = 0.05
## power = 0.9
## alternative = two.sidedA fenti outputból kiolvasható, hogy 8 elemű mintára van szükségünk.
Alternatíva az egymintás t-próba végrehajtására. Egymintás t-próbát az lsr csomag oneSampleTTest() függvényével, valamint a lessR csomag ttest() függvényével is végrehajthatunk. Mindkét alternatíva jelentősen gazdagabb outputot szolgáltat az alapértelmezett t.test() függvényhez képest.
library(lsr)
oneSampleTTest(x = x, mu = 1) # egymintás t-próba végrehajtása az lsr csomag oneSampleTTest() függvényével##
## One sample t-test
##
## Data variable: x
##
## Descriptive statistics:
## x
## mean 1.463
## std dev. 0.341
##
## Hypotheses:
## null: population mean equals 1
## alternative: population mean not equal to 1
##
## Test results:
## t-statistic: 4.298
## degrees of freedom: 9
## p-value: 0.002
##
## Other information:
## two-sided 95% confidence interval: [1.219, 1.707]
## estimated effect size (Cohen's d): 1.359library(lessR)
ttest(x = x, mu = 1) # egymintás t-próba végrehajtása a lessR csomag ttest() függvényével##
##
## ------ Description ------
##
## x: n.miss = 0, n = 10, mean = 1.463, sd = 0.341
##
##
## ------ Normality Assumption ------
##
## Null hypothesis is a normal distribution of x.
## Shapiro-Wilk normality test: W = 0.9628, p-value = 0.8176
##
##
## ------ Inference ------
##
## t-cutoff: tcut = 2.262
## Standard Error of Mean: SE = 0.108
##
## Hypothesized Value H0: mu = 1
## Hypothesis Test of Mean: t-value = 4.298, df = 9, p-value = 0.002
##
## Margin of Error for 95% Confidence Level: 0.244
## 95% Confidence Interval for Mean: 1.219 to 1.707
##
##
## ------ Effect Size ------
##
## Distance of sample mean from hypothesized: 0.463
## Standardized Distance, Cohen's d: 1.359
##
##
## ------ Graphics Smoothing Parameter ------
##
## Density bandwidth for 0.245
## --------------------------------------------------
3.5 Páros t-próba
A páros t-próba két összetartozó minta esetén a különbségváltozó várható értékének (\(\mu_d=\mu_1-\mu_2\)) adott értéktől (\(d_0\)) való eltérését vizsgálja.
Alkalmazási feltételek:
- véletlen, összetartozó (páros) minta: \((X_1, X_2)\)
- az \(X_1\) és \(X_2\) normális eloszlású (elegendő, ha a \(X_1-X_2\) különbségváltozó normális eloszlású)
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu_d=d_0\)
- ha \(d_0=0\), akkor \(H_0: \mu_1-\mu_2=0\) vagy \(H_0: \mu_1=\mu_2\) formában is írható
- Ellenhipotézis:
- \(H_1: \mu_d \neq d_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_d < d_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_d > d_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
- ha \(d_0=0\), akkor a fenti ellenhipotézisek:
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_1<\mu_2\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_1>\mu_2\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
\[T=\frac{(\bar{X_1}-\bar{X_2})-d_0}{s_d/\sqrt{n}} \sim t(n-1)\]
3.5.1 Példa: a vizualizáció és fájdalom kontrolálása.
Önként jelentkezőket arra kértek, hogy tegyék jeges vízbe a kezüket. Az egyik esetben azt kérték tőlük, hogy képzeljenek el egy kellemes körülményt (pl. pálmafák, napsütés, tengerpart), majd később megismételték a kísérletet úgy, hogy egy kellemetlen körülmény elképzelésére kérték őket (pl. statisztikai próbák végrehajtása). Mindkét esetben megmérték, hogy hány másodperc elteltével veszik ki a kezüket a jeges vízből. Vizsgáljuk meg, hogy van-e hatása az elképzelt körülménynek (vizualizáció) a fájdalom tűrésére!
Forrás: (Dancey and Reidy 2011, 230)
A két vizualizációs módhoz (kellemes és kellemetlen körülmény elképzelése) tartozó két változó várható értékének egyezését vizsgáljuk páros t-próbával:
- \(H_0: \mu_1=\mu_2\)
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis)
Adatok beolvasása. Első lépésként végezzük el az adatok beolvasását egy d adattáblába:
d <- read.table(file = textConnection("
participant stat beach
1 5 7
2 7 15
3 3 6
4 6 7
5 10 12
6 4 12
7 7 10
8 8 14
9 8 13
10 15 7
"), header=T, sep="")
d$participant <- factor(d$participant)
str(d) # az adattábla szerkezete## 'data.frame': 10 obs. of 3 variables:
## $ participant: Factor w/ 10 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10
## $ stat : int 5 7 3 6 10 4 7 8 8 15
## $ beach : int 7 15 6 7 12 12 10 14 13 7d # a beolvasott adattábla## participant stat beach
## 1 1 5 7
## 2 2 7 15
## 3 3 3 6
## 4 4 6 7
## 5 5 10 12
## 6 6 4 12
## 7 7 7 10
## 8 8 8 14
## 9 9 8 13
## 10 10 15 7A páros adatok vizsgálatához is előkészítjük adatainkat. A PairedData csomag paired() függvényét használjuk az átalakításhoz. A későbbiekben a d.paired adattáblát is használni fogjuk.
library(PairedData)
d.paired <- with(d, paired(stat, beach)) # adatelőkészítés a PairedData csomag használatához
d.paired # a páros minta## Object of class "paired"
## stat beach
## 1 5 7
## 2 7 15
## 3 3 6
## 4 6 7
## 5 10 12
## 6 4 12
## 7 7 10
## 8 8 14
## 9 8 13
## 10 15 7A páros adatokból egy hosszú adattáblát is létrehozunk a reshape2 csomag melt() függvényével. A továbbiakban a d.l adattáblát is fogjuk használni.
library(reshape2)
d.l <- melt(d, id.vars = "participant", variable.name = "group", value.name = "seconds")
d.l## participant group seconds
## 1 1 stat 5
## 2 2 stat 7
## 3 3 stat 3
## 4 4 stat 6
## 5 5 stat 10
## 6 6 stat 4
## 7 7 stat 7
## 8 8 stat 8
## 9 9 stat 8
## 10 10 stat 15
## 11 1 beach 7
## 12 2 beach 15
## 13 3 beach 6
## 14 4 beach 7
## 15 5 beach 12
## 16 6 beach 12
## 17 7 beach 10
## 18 8 beach 14
## 19 9 beach 13
## 20 10 beach 7Páros t-próba végrehajtása. A páros t-próba végrehajtását a t.test() függvénnyel kezdeményezhetjük. A páros mintát megadjuk az x= és y= argumentumokban, valamint a paired=T paraméterrel a t-próba páros típusát definiáljuk.
t.test(x = d$stat, y = d$beach, paired = T) # páros t-próba végrehajtása##
## Paired t-test
##
## data: d$stat and d$beach
## t = -2.0647, df = 9, p-value = 0.06895
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -6.2868382 0.2868382
## sample estimates:
## mean of the differences
## -3A páros t-próba értékelése. A páros t-próba eredménye alapján azt mondhatjuk, hogy nincs elegendő bizonyítékunk arra, hogy a két vizualizációs módban eltérő lenne a fájdalom kontrolálásának mértéke (\(t (9)=-2,0647\); \(p=0,06895\)).
A páros t-próba kézi számolása. A próba outputjában szereplő értékeket magunk is kiszámolhatjuk:
atlag <- mean(d$stat - d$beach, na.rm = T) # a különbségváltozó mintaátlaga
szoras <- sd(d$stat - d$beach, na.rm = T) # a különbségváltozó mintabeli szórása
n <- sum(!is.na(d$stat)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
d.0 <- 0 # a különbség hipotetikus várható értéke
t <- (atlag-d.0)/SE # próbastatisztika értéke
t # próbastatisztika értékének kiírása## [1] -2.0647422*(1-pt(q = abs(t), df = n-1)) # a p érték kétoldali próba esetén## [1] 0.06894876Konfidenciaintervallum kézi számolása páros t-próba esetén. Az \(\left( 1-\alpha \right)\) konfidenciaintervallum kiszámítása nem tér el az egymintás esettől, csak most a különbségváltozóval kell számolnunk.
\[\left] (\bar{X_1}-\bar{X_2})-t_{\alpha, df}\frac{s_d}{\sqrt{n}}, (\bar{X_1}-\bar{X_2})+t_{\alpha, df}\frac{s_d}{\sqrt{n}} \right[\]
# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- mean(d$stat - d$beach, na.rm = T) # a különbségváltozó mintaátlaga
szoras <- sd(d$stat - d$beach, na.rm = T) # a különbségváltozó mintabeli szórása
n <- sum(!is.na(d$stat)) # mintaelemszám
SE <- szoras/sqrt(n) # standard hiba
alfa <- 0.05 # alfa=1-0.95
t.alfa <- qt(p = 1-alfa/2, df = n-1) # t_{alfa,df} kritikusérték
atlag + c(-t.alfa*SE, t.alfa*SE) # a 95%-os konf.intv. határai ## [1] -6.2868382 0.2868382Alkalmazási feltételek ellenőrzése páros t-próbához. A páros t-próba feltételeinek ellenőrzése történhet Shapiro-Wilk próbával:
shapiro.test(d$stat) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: d$stat
## W = 0.91263, p-value = 0.2995shapiro.test(d$beach) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: d$beach
## W = 0.89146, p-value = 0.1761shapiro.test(d$stat-d$beach) # normalitás ellenőrzése Shapiro-Wilk-próbával##
## Shapiro-Wilk normality test
##
## data: d$stat - d$beach
## W = 0.84996, p-value = 0.05803A fenti outputokból kiolvasható, hogy a két változó és a különbségváltozó normalitását nem tudjuk megcáfolni.
Leíró statisztikai vizsgálatok páros t-próbához. A PairedData csomag summary() függvénye az előkészített d.paired adattábla esetén a páros mintáknál megszokott mutatókat jeleníti meg. Mutatókat kapunk a két összetartozó mintára, azok különbségére és átlagára is.
library(PairedData)
PairedData::summary(d.paired) # mutatók a páros mintára ## $stat
## n mean median trim sd IQR (*) median ad (*)
## stat (x) 10 7.3 7.0 6.833333 3.400980 2.038547 2.2239
## beach (y) 10 10.3 11.0 10.166667 3.335000 4.262417 5.1891
## x-y 10 -3.0 -3.0 -3.500000 4.594683 2.779837 2.9652
## (x+y)/2 10 8.8 9.5 9.250000 2.463060 3.057821 2.2239
## mean ad (*) sd(w) min max
## stat (x) 2.882623 2.083519 3.0 15
## beach (y) 3.634611 4.372276 6.0 15
## x-y 3.759942 2.848838 -8.0 8
## (x+y)/2 2.631960 3.210393 4.5 11
##
## $cor
## cor wcor
## (x,y) 0.06955301 0.4824492Grafikus lehetőséges páros t-próbára. A PairedData csomag az előkészített d.paired adattáblára a grafikus megjelenítést is lehetővé tesz. Rajzolhatunk kétdimenziós pontdiagramot, valamint dobozdiagramot a párosított mintaelemek megjelenítésével is.
library(gridExtra)
library(PairedData)
p1 <- plot(d.paired) + theme_bw() # kétdimenziós pontdiagram
p2 <- plot(d.paired, type="profile") + theme_bw() # dobozdiagram és a páros mintaelemek
grid.arrange(p1, p2, ncol = 2) # ábrák megjelenítése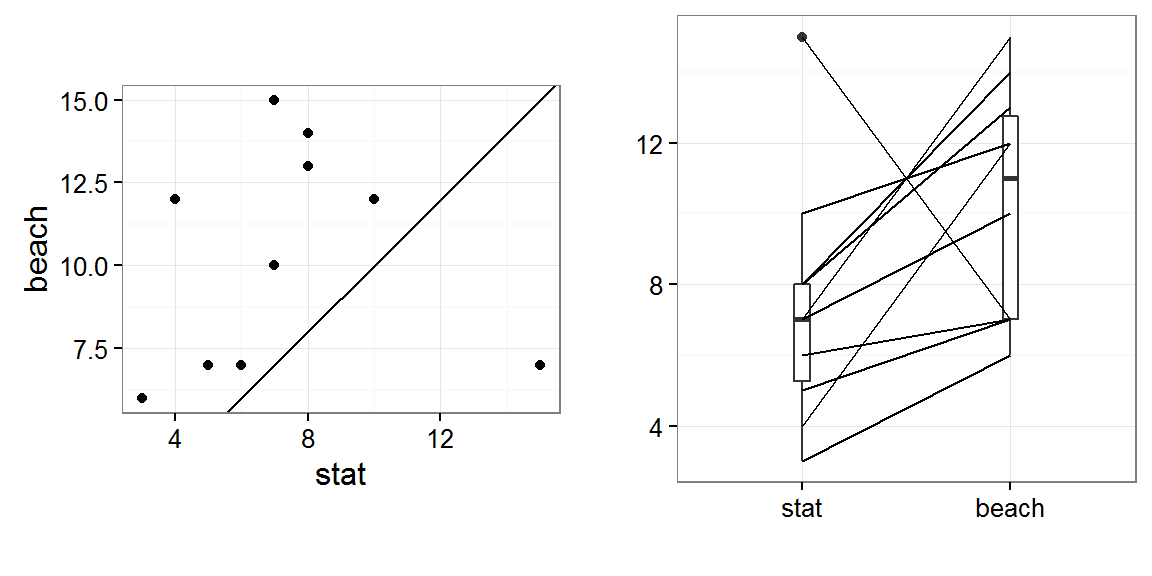
A hatás mértékének meghatározása páros t-próbában. A páros t-próbához tartozó hatásméret kiszámítása a következő összefüggéssel történik.
\[d=\left|\frac{(\bar{X_1}-\bar{X_2})-d_0}{s_d}\right|\]
A hatásmérték kiszámítása az lsr csomag cohensD() függvényével és kézzel is könnyen kiszámolható:
library(lsr)
cohensD(x = d$stat, y = d$beach, method = "paired")## [1] 0.6529286atlag <- mean(d$stat - d$beach, na.rm = T) # a különbségváltozó mintaátlaga
szoras <- sd(d$stat - d$beach, na.rm = T) # a különbségváltozó mintabeli szórása
atlag / szoras # a Cohen-d kézi kiszámolása## [1] -0.6529286A statisztikai erő meghatározása a páros t-próbában.
A statisztikai erő meghatározásához a pwr csomag pwr.t.test() függvényét használjuk. A bemenő paraméterek:
n=- a mintaelemszámd=- a hatás nagyságasig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formájatype=- a t próba típusa
library(pwr)
pwr.t.test(n = 10, d = 0.653, sig.level = 0.05, alternative = "two.sided", type = "paired")##
## Paired t test power calculation
##
## n = 10
## d = 0.653
## sig.level = 0.05
## power = 0.4540401
## alternative = two.sided
##
## NOTE: n is number of *pairs*Az output alapján azt mondhatjuk, hogy a próba statisztikai ereje 45,4%-os.
Mintaelemszám meghatározása páros t-próbához. Ha 90%-os statisztikai erőre van szükségünk, akkor ugyanilyen hatásnagyság kimutatásához (\(d=0,653\)), mekkora mintaelemszámra van szükség?
library(pwr)
pwr.t.test(power = 0.9, d = 0.653, sig.level = 0.05, alternative = "two.sided", type = "paired")##
## Paired t test power calculation
##
## n = 26.63692
## d = 0.653
## sig.level = 0.05
## power = 0.9
## alternative = two.sided
##
## NOTE: n is number of *pairs*A fenti outputból kiolvasható, hogy 27 elemű mintára van szükségünk.
Alternatívák a páros t-próbára. Páros t-próbát a d.l hosszú adattábla segítségével is végrehajthatunk. A t.test() és az lsr csomag pairedSamplesTTest() függvénye is hosszú adattáblát vár, így a formula= és data= argumentumokat kell megadnunk. A lessR csomag ttest() függvényében a már korábban látott x= és y= argumentumok várják a két összetartozó mintát.
t.test(formula = seconds ~ group, data=d.l, paired = T)##
## Paired t-test
##
## data: seconds by group
## t = -2.0647, df = 9, p-value = 0.06895
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -6.2868382 0.2868382
## sample estimates:
## mean of the differences
## -3library(lsr)
pairedSamplesTTest(formula = seconds ~ group, data=d.l, id="participant")##
## Paired samples t-test
##
## Outcome variable: seconds
## Grouping variable: group
## ID variable: participant
##
## Descriptive statistics:
## stat beach difference
## mean 7.300 10.300 -3.000
## std dev. 3.401 3.335 4.595
##
## Hypotheses:
## null: population means equal for both measurements
## alternative: different population means for each measurement
##
## Test results:
## t-statistic: -2.065
## degrees of freedom: 9
## p-value: 0.069
##
## Other information:
## two-sided 95% confidence interval: [-6.287, 0.287]
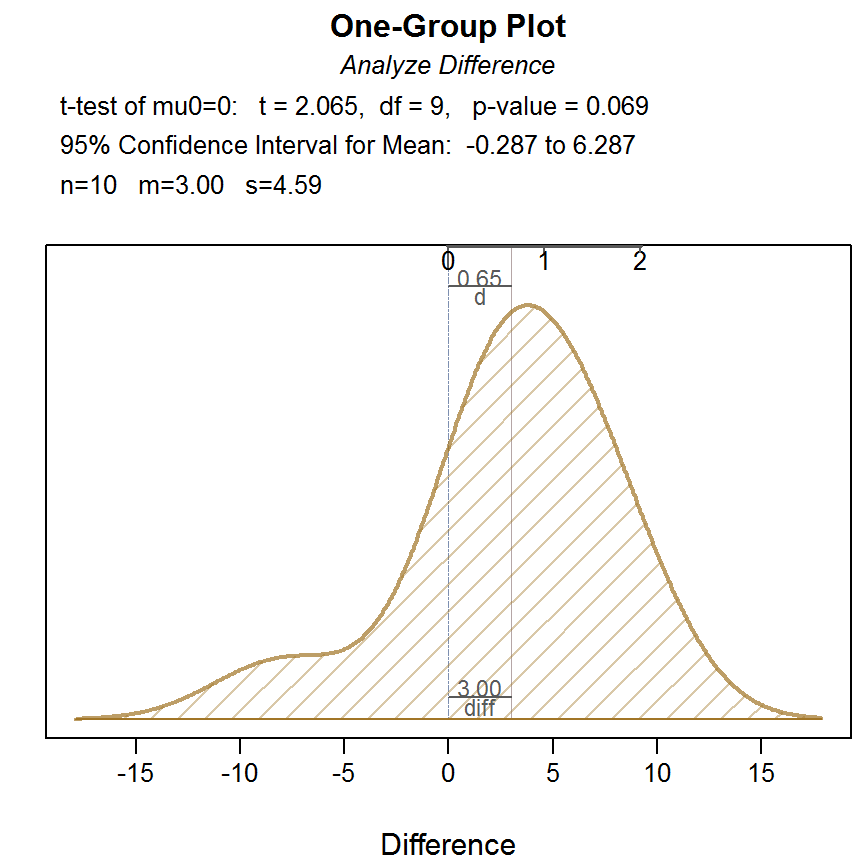
## estimated effect size (Cohen's d): 0.653library(lessR)
ttest(x = stat, y = beach, data = d, paired = T)##
##
## ------ Description ------
##
## Difference: n.miss = 0, n = 10, mean = 3.00, sd = 4.59
##
##
## ------ Normality Assumption ------
##
## Null hypothesis is a normal distribution of Difference.
## Shapiro-Wilk normality test: W = 0.85, p-value = 0.058
##
##
## ------ Inference ------
##
## t-cutoff: tcut = 2.262
## Standard Error of Mean: SE = 1.45
##
## Hypothesized Value H0: mu = 0
## Hypothesis Test of Mean: t-value = 2.065, df = 9, p-value = 0.069
##
## Margin of Error for 95% Confidence Level: 3.29
## 95% Confidence Interval for Mean: -0.29 to 6.29
##
##
## ------ Effect Size ------
##
## Distance of sample mean from hypothesized: 3.00
## Standardized Distance, Cohen's d: 0.65
##
##
## ------ Graphics Smoothing Parameter ------
##
## Density bandwidth for 3.30
## --------------------------------------------------


3.6 Kétmintás t-próba
Azt teszteljük, hogy két független változó várható értékének különbsége (\(\mu_d=\mu_1-\mu_2\)) eltér-e egy adott értéktől (\(d_0\)). Feltételezzük a normális eloszlást és ismeretlen populációbeli szórások egyenlőségét.
Alkalmazási feltételek:
- két véletlen független minta: \(X_1\) és \(X_2\)
- \(X_1\) és \(X_2\) normális eloszlású a populációban
- az ismeretlen populációbeli szórások egyenlőek: \(\sigma_1 = \sigma_2\)
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu_d=d_0\)
- ha \(d_0=0\), akkor \(H_0: \mu_1-\mu_2=0\) vagy \(H_0: \mu_1=\mu_2\) formában is írható
- Ellenhipotézis:
- \(H_1: \mu_d \neq d_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_d < d_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_d > d_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
- ha \(d_0=0\), akkor a fenti ellenhipotézisek:
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_1<\mu_2\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_1>\mu_2\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
\[s_p^2=\frac{(n_1 -1)s_1^2 + (n_2 -1)s_2^2}{n_1 + n_2 - 2}, T=\frac{(\bar{X_1}-\bar{X_2})-d_0}{\sqrt{\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}}} \sim t(n_1 + n_2 -2)\]
3.6.1 Példa: zaj hatása a rövidtávú memóriára
Huszonnégy ember részt vett egy kísérletben, amelyben annak megállapítását tűzték ki célul, hogy a háttérzaj (zene, ajtócsapódás, kávékészítés zaja stb.) hogyan befolyásolja a rövid távú memóriát (szavak visszahívását). A résztvevők fele (
NOISEcsoport) megpróbált memorizálni 2 perc alatt egy 20 szavas listát, miközben fülhallgatón keresztül az előre felvett zaj szólt. A többi résztvevő is viselt fülhallgatót (NO NOISEcsoport), de ők nem hallottak zajt a szavak memorizálása közben. Közvetlenül ezután megállapították, hogy hány szóra emlékeztek vissza. Vizsgáljuk meg, hogy van-e eltérés a visszahívott szavak számában a két kondícióban, vagyis a zajnak van-e hatása a rövidtávú memóriára! Forrás: (Dancey and Reidy 2011, 212)
A két kondícióhoz (NOISE és NO NOISE) tartozó visszahívott szavak száma változók várható értékének egyezését vizsgáljuk kétmintás t-próbával:
- \(H_0: \mu_1=\mu_2\)
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis)
Adatok beolvasása. Végezzük el az adatok beolvasását a d adattáblába. Az adatok a két csoport azonos elemszáma miatt kényelmesen tárolhatók széles adattáblában, de a reshape2 csomag melt() függvényével átalakítjuk szükséges hosszú formátumúvá.
d <- read.table(file = textConnection("
NOISE NO.NOISE
5.00 15.00
10.00 9.00
6.00 16.00
6.00 15.00
7.00 16.00
3.00 18.00
6.00 17.00
9.00 13.00
5.00 11.00
10.00 12.00
11.00 13.00
9.00 11.00
"), header=T, sep="")
library(reshape2)
d <- melt(d, id.vars = NULL, variable.name = "group", value.name = "words") # szélesből hosszú átalakítás
str(d) # az adattábla szerkezete## 'data.frame': 24 obs. of 2 variables:
## $ group: Factor w/ 2 levels "NOISE","NO.NOISE": 1 1 1 1 1 1 1 1 1 1 ...
## $ words: num 5 10 6 6 7 3 6 9 5 10 ...d # a beolvasott adattábla## group words
## 1 NOISE 5
## 2 NOISE 10
## 3 NOISE 6
## 4 NOISE 6
## 5 NOISE 7
## 6 NOISE 3
## 7 NOISE 6
## 8 NOISE 9
## 9 NOISE 5
## 10 NOISE 10
## 11 NOISE 11
## 12 NOISE 9
## 13 NO.NOISE 15
## 14 NO.NOISE 9
## 15 NO.NOISE 16
## 16 NO.NOISE 15
## 17 NO.NOISE 16
## 18 NO.NOISE 18
## 19 NO.NOISE 17
## 20 NO.NOISE 13
## 21 NO.NOISE 11
## 22 NO.NOISE 12
## 23 NO.NOISE 13
## 24 NO.NOISE 11A kétmintás t-próba végrehajtása. Kétmintás t-próbát a t.test() függvénnyel hajthatunk végre. A d hosszú adattábla két oszlopából készítünk formulát a formula= argumentum számára. A kétmintás t-próba végrehajtásához szükséges szóráshomogenitást a var.equal=T argumentum megadásával biztosítjuk.
t.test(formula = words ~ group, data = d, var.equal = T)##
## Two Sample t-test
##
## data: words by group
## t = -6.1366, df = 22, p-value = 0.000003548
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -8.808169 -4.358498
## sample estimates:
## mean in group NOISE mean in group NO.NOISE
## 7.25000 13.83333A kétmintás t-próba értékelése. A kétmintás t-próba eredménye alapján azt mondhatjuk, hogy a zajnak szignifikáns hatása van a rövidtávú memóriára, vagyis a visszahívott szavak száma szignifikánsan eltér a két kondícióban (\(t(22)=-6,1366\); \(p<0,001\)).
A kétmintás t-próba kézi számolása. A próba outputjában szereplő értékeket magunk is kiszámolhatjuk:
x.1 <- d$words[ d$group %in% "NOISE"] # 1. adatminta
x.2 <- d$words[ d$group %in% "NO.NOISE"] # 2. adatminta
atlag <- mean(x.1, na.rm = T) - mean(x.2, na.rm = T) # a mintaátlagok különbsége
szoras.1 <- sd(x.1, na.rm = T) # 1. adatminta szórása
szoras.2 <- sd(x.2, na.rm = T) # 2. adatminta szórása
n.1 <- sum(!is.na(x.1)) # 1. minta elemszáma
n.2 <- sum(!is.na(x.2)) # 2. minta elemszáma
s.p <- sqrt(((n.1-1)*szoras.1^2+(n.2-1)*szoras.2^2)/(n.1 + n.2 - 2)) # pooled szórás
SE <- s.p*sqrt(1/n.1 + 1/n.2) # standard hiba a különbségre
d.0 <- 0 # hipotetikus várható érték
t <- (atlag-d.0)/SE # próbastatisztika értéke
t # próbastatisztika értékének kiírása## [1] -6.1366322*(1-pt(q = abs(t), df = n.1 + n.2 - 2)) # a p érték kétoldali próba esetén## [1] 0.000003547597Konfidenciaintervallum kézi számolása kétmintás t-próbához. A próba outputjában szereplő konfidenciaintervallum határait a DescTools csomag MeanDiffCI() függvényével is meghatározhatjuk, de a kézi kiszámolása sem túl bonyolult. A várható értékre vonatkozó \(\left(1-\alpha \right)\) megbízhatóságú konfidenciaintervallum:
\[\left] (\bar{X_1}-\bar{X_2})-t_{\alpha, df}\sqrt{\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}}, (\bar{X_1}-\bar{X_2})+t_{\alpha, df}\sqrt{\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}} \right[\]
A MeanDiffCI() függvény argumentumában meg kell adnunk a formula=words ~ group argumentumban két adatmintát, és az adattábla nevét a data= argumentumban, valamint opcionálisan a megbízhatósági szintet (conf.level=) és a hiányzó értékek eltávolítására használatos na.rm=T paramétert. A MeanDiffCI() függvény nem tételezi fel a populációbeli szórások egyezését, így a következő fejezetben ismertett Welch-féle d-próbához tartozó konfidenciaintervallumot szolgáltatja.
library(DescTools)
MeanDiffCI(formula = words ~ group, data = d)## meandiff lwr.ci upr.ci
## -6.583333 -8.809498 -4.357169# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
x.1 <- d$words[ d$group %in% "NOISE"] # 1. adatminta
x.2 <- d$words[ d$group %in% "NO.NOISE"] # 2. adatminta
atlag <- mean(x.1, na.rm = T) - mean(x.2, na.rm = T) # a mintaátlagok különbsége
szoras.1 <- sd(x.1, na.rm = T) # 1. adatminta szórása
szoras.2 <- sd(x.2, na.rm = T) # 2. adatminta szórása
n.1 <- sum(!is.na(x.1)) # 1. minta elemszáma
n.2 <- sum(!is.na(x.2)) # 2. minta elemszáma
s.p <- sqrt(((n.1-1)*szoras.1^2+(n.2-1)*szoras.2^2)/(n.1 + n.2 - 2)) # pooled szórás
SE <- s.p*sqrt(1/n.1 + 1/n.2) # standard hiba a különbségre
alfa <- 0.05 # alfa=1-0.95
t.alfa <- qt(p = 1-alfa/2, df = n.1 + n.2 - 2) # t_{alfa,df} kritikusérték
atlag + c(-t.alfa*SE, t.alfa*SE) # a 95%-os konf.intv. határai ## [1] -8.808169 -4.358498Alkalmazási feltételek ellenőrzése. A kétmintás t-próba feltételeinek ellenőrzése:
by(d$words, d$group, shapiro.test) # normalitás ellenőrzése Shapiro-Wilk-próbával## d$group: NOISE
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93755, p-value = 0.467
##
## --------------------------------------------------------
## d$group: NO.NOISE
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96299, p-value = 0.8255var.test(words ~ group, data = d) # F-próba a varianciák egyezőségére##
## F test to compare two variances
##
## data: words by group
## F = 0.81574, num df = 11, denom df = 11, p-value = 0.7415
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.2348324 2.8336250
## sample estimates:
## ratio of variances
## 0.8157371A két kondícióban a változók normalitását nem tudjuk megcáfolni (Shapiro-Wilk-próba: \(p=0,467\) és \(p=0,8255\)), valamint a populációbeli szórások egyezését vizsgáló F-próba (\(F(11,11)=0,8157; p=0,7415\)) is megerősít minket abban, hogy a kétmintás t-próba alkalmazási feltételei teljesülnek.
Leíró statisztikai mutatók kétmintás t-próbához. A kétmintás t-próbához kapcsolódó leíró statisztikai vizsgálatok:
library(psych)
describeBy(x = d$words, group = d$group)## group: NOISE
## vars n mean sd median trimmed mad min max range skew kurtosis se
## 1 1 12 7.25 2.49 6.5 7.3 2.97 3 11 8 0 -1.45 0.72
## --------------------------------------------------------
## group: NO.NOISE
## vars n mean sd median trimmed mad min max range skew kurtosis se
## 1 1 12 13.83 2.76 14 13.9 2.97 9 18 9 -0.15 -1.36 0.8library(DescTools)
Desc(words ~ group, data=d)## -------------------------------------------------------------------------
## words ~ group
##
## Summary:
## n pairs: 24, valid: 24 (100.0%), missings: 0 (0.0%), groups: 2
##
##
## NOISE NO.NOISE
## mean 7.2500000 13.8333333
## median 6.5000000 14.0000000
## sd 2.4908925 2.7579087
## IQR 3.5000000 4.2500000
## n 12 12
## np 50.0000000% 50.0000000%
## NAs 0 0
## 0s 0 0
##
## Kruskal-Wallis rank sum test:
## Kruskal-Wallis chi-squared = 15.075, df = 1, p-value = 0.0001033library(pastecs)
print(by(d$words, d$group, stat.desc, norm = T), digits = 2)## d$group: NOISE
## nbr.val nbr.null nbr.na min max
## 12.0000 0.0000 0.0000 3.0000 11.0000
## range sum median mean SE.mean
## 8.0000 87.0000 6.5000 7.2500 0.7191
## CI.mean.0.95 var std.dev coef.var skewness
## 1.5826 6.2045 2.4909 0.3436 -0.0020
## skew.2SE kurtosis kurt.2SE normtest.W normtest.p
## -0.0016 -1.4506 -0.5886 0.9376 0.4670
## --------------------------------------------------------
## d$group: NO.NOISE
## nbr.val nbr.null nbr.na min max
## 12.00 0.00 0.00 9.00 18.00
## range sum median mean SE.mean
## 9.00 166.00 14.00 13.83 0.80
## CI.mean.0.95 var std.dev coef.var skewness
## 1.75 7.61 2.76 0.20 -0.15
## skew.2SE kurtosis kurt.2SE normtest.W normtest.p
## -0.12 -1.36 -0.55 0.96 0.83Grafikus vizsgálatok kétmintás t-próbához.
library(ggplot2)
library(gridExtra)
p1 <- ggplot(data=d, aes(x=group, y=words, color=group)) + # átlagok és konfidenciaintervallumok
stat_summary(fun.y=mean, geom="point", size=4, shape=21, fill="white") +
stat_summary(fun.data=mean_cl_normal, geom="errorbar", size=1, width=0.1) +
theme_bw() + coord_cartesian(ylim=c(4, 18))
p2 <- ggplot(data=d, aes(x=group, y=words, color=group)) + # dobozdiagramok
geom_boxplot() + theme_bw() + coord_cartesian(ylim=c(4, 18))
p3 <- ggplot(data=d, aes(x=words)) + # hisztogram
geom_histogram(binwidth = 2, col="#00ADEE", fill="#C7EBFC", size=1) + theme_bw() + facet_wrap(~group, nrow=2)
p4 <- ggplot(data = d, aes(x=words)) + # simított hisztogram
geom_density(aes(fill=group, colour=group), size=1, alpha=0.5) + theme_bw()
grid.arrange(p1, p2, p3, p4, ncol=2) # ábrák megjelenítése
A hatás nagyságának meghatározása kétmintás t-próbában. Kétmintás t-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{(\bar{X_1}-\bar{X_2})-d_0}{s_p}\right|\]
library(lsr)
cohensD(formula = words ~ group, data=d, method = "pooled")## [1] 2.50527x.1 <- d$words[ d$group %in% "NOISE"] # 1. adatminta
x.2 <- d$words[ d$group %in% "NO.NOISE"] # 2. adatminta
atlag <- mean(x.1, na.rm = T) - mean(x.2, na.rm = T) # a mintaátlagok különbsége
szoras.1 <- sd(x.1, na.rm = T) # 1. adatminta szórása
szoras.2 <- sd(x.2, na.rm = T) # 2. adatminta szórása
n.1 <- sum(!is.na(x.1)) # 1. minta elemszáma
n.2 <- sum(!is.na(x.2)) # 2. minta elemszáma
s.p <- sqrt(((n.1-1)*szoras.1^2+(n.2-1)*szoras.2^2)/(n.1 + n.2 - 2)) # pooled szórás
atlag / s.p # Cohen-d kiszámítása## [1] -2.50527library(powerAnalysis)
ES.t.two(m1 = mean(x.1, na.rm = T), m2 = mean(x.2, na.rm = T), sd1 = szoras.1, sd2 = szoras.2, n1 = n.1, n2 = n.2)##
## effect size (Cohen's d) of independent two-sample t test
##
## d = 2.50527
## alternative = two.sided
##
## NOTE: The alternative hypothesis is m1 != m2
## small effect size: d = 0.2
## medium effect size: d = 0.5
## large effect size: d = 0.8A Cohen-d értéke 2,5, ami azt mutatja, hogy a hatás nagy mértékű.
Az erő meghatározása kétmintás t-próbában A statisztikai erő meghatározásához a powerAnalysis csomag power.t() függvényét használjuk. A bemenő paraméterek:
es=- a hatás nagyságan=- a összmintaelemszámtype=- az elemszámok különbözőségeratio=- az elemszámok aránya a két csoportbansig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formája
A pwr csomag pwr.t.test() függvényével is elvégezzük a számolást.
library(powerAnalysis)
power.t(es = 2.5, n=12, sig.level=0.05, type="two", alternative = "two.sided")##
## Two-sample (equal size) t test power calculation
##
## es = 2.5
## n = 12
## power = 0.9999478
## sig.level = 0.05
## alternative = two.sided
##
## NOTE: n is number in *each* grouplibrary(pwr)
pwr.t.test(d = 2.5, n = 12, sig.level = 0.05, type = "two.sample", alternative = "two.sided")##
## Two-sample t test power calculation
##
## n = 12
## d = 2.5
## sig.level = 0.05
## power = 0.9999478
## alternative = two.sided
##
## NOTE: n is number in *each* groupAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 99,99%-os.
Mintaelemszám meghatározása a kétmintás t-próbában. Ha 95%-os statisztikai erő elegendő a próba végrehajtása során, akkor ugyanilyen hatásnagyság kimutatásához (\(d=2,5\)), mekkora mintaelemszámra van szükség?
library(powerAnalysis)
power.t(es = 2.5, power = 0.95, sig.level=0.05, type="two", alternative="two.sided")##
## Two-sample (equal size) t test power calculation
##
## es = 2.5
## n = 5.343538
## power = 0.95
## sig.level = 0.05
## alternative = two.sided
##
## NOTE: n is number in *each* grouplibrary(pwr)
pwr.t.test(d = 2.5, power = 0.95, sig.level = 0.05, type = "two.sample", alternative = "two.sided")##
## Two-sample t test power calculation
##
## n = 5.343548
## d = 2.5
## sig.level = 0.05
## power = 0.95
## alternative = two.sided
##
## NOTE: n is number in *each* groupLátható, hogy a 95%-os statisztikai erő eléréséhez (kerekítve) 5 elemű mintára van szükség.
Alternatívák a kétmintás t-próbára. A kétmintás t-próbát az lsr csomag pairedSamplesTTest() függvényével, valamint a lessR csomag ttest() függvényével is végrehajthatunk. Ezek outputja más próbák végrehajtását is tartalmazhatja.
library(lsr)
independentSamplesTTest(words ~ group, data = d, var.equal = T)##
## Student's independent samples t-test
##
## Outcome variable: words
## Grouping variable: group
##
## Descriptive statistics:
## NOISE NO.NOISE
## mean 7.250 13.833
## std dev. 2.491 2.758
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: -6.137
## degrees of freedom: 22
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [-8.808, -4.358]
## estimated effect size (Cohen's d): 2.505library(lessR)
ttest(words ~ group, data = d)##
## Compare words across group levels NO.NOISE and NOISE
## ------------------------------------------------------------
##
##
## ------ Description ------
##
## words for group NO.NOISE: n.miss = 0, n = 12, mean = 13.83, sd = 2.76
## words for group NOISE: n.miss = 0, n = 12, mean = 7.25, sd = 2.49
##
## Within-group Standard Deviation: 2.63
##
##
## ------ Assumptions ------
##
## Note: These hypothesis tests can perform poorly, and the
## t-test is typically robust to violations of assumptions.
## Use as heuristic guides instead of interpreting literally.
##
## Null hypothesis, for each group, is a normal distribution of words.
## Group NO.NOISE Shapiro-Wilk normality test: W = 0.963, p-value = 0.825
## Group NOISE Shapiro-Wilk normality test: W = 0.938, p-value = 0.467
##
## Null hypothesis is equal variances of words, i.e., homogeneous.
## Variance Ratio test: F = 7.61/6.20 = 1.23, df = 11;11, p-value = 0.741
## Levene's test, Brown-Forsythe: t = 0.445, df = 22, p-value = 0.660
##
##
## ------ Inference ------
##
## --- Assume equal population variances of words for each group
##
## t-cutoff: tcut = 2.074
## Standard Error of Mean Difference: SE = 1.07
##
## Hypothesis Test of 0 Mean Diff: t = 6.137, df = 22, p-value = 0.000
##
## Margin of Error for 95% Confidence Level: 2.22
## 95% Confidence Interval for Mean Difference: 4.36 to 8.81
##
##
## --- Do not assume equal population variances of words for each group
##
## t-cutoff: tcut = 2.075
## Standard Error of Mean Difference: SE = 1.07
##
## Hypothesis Test of 0 Mean Diff: t = 6.137, df = 21.776, p-value = 0.000
##
## Margin of Error for 95% Confidence Level: 2.23
## 95% Confidence Interval for Mean Difference: 4.36 to 8.81
##
##
## ------ Effect Size ------
##
## --- Assume equal population variances of words for each group
##
## Sample Mean Difference of words: 6.58
## Standardized Mean Difference of words, Cohen's d: 2.51
##
## 95% Confidence Interval for smd: 1.40 to 3.58
##
##
## ------ Practical Importance ------
##
## Minimum Mean Difference of practical importance: mmd
## Minimum Standardized Mean Difference of practical importance: msmd
## Neither value specified, so no analysis
##
##
## ------ Graphics Smoothing Parameter ------
##
## Density bandwidth for group NO.NOISE: 1.91
## Density bandwidth for group NOISE: 1.73
## --------------------------------------------------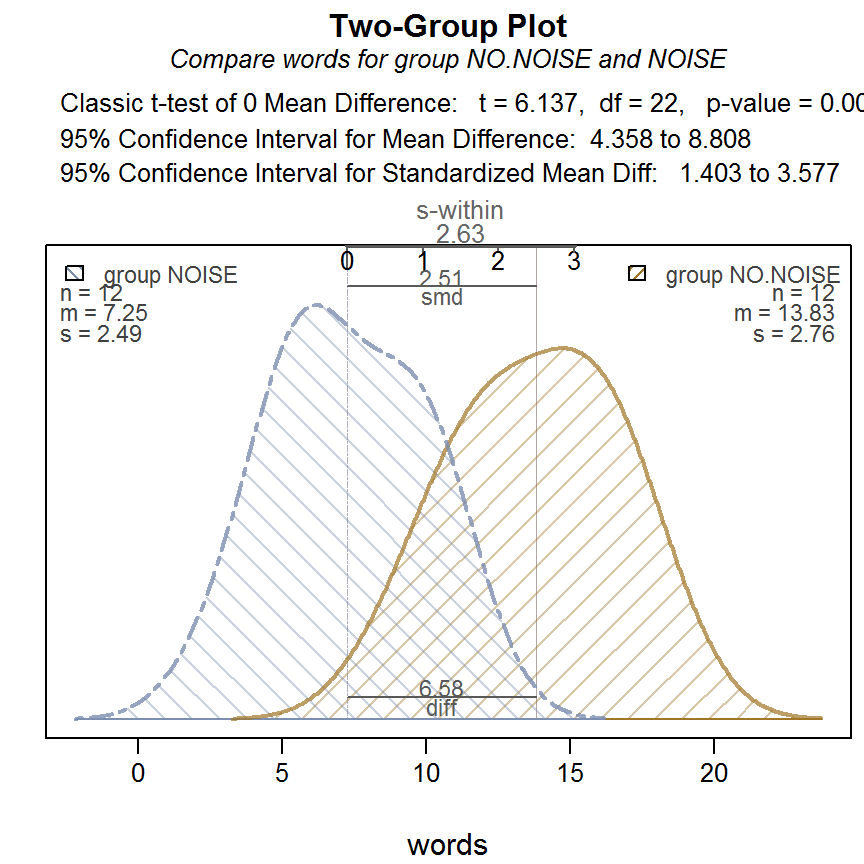
##
## [smd CI with Ken Kelley's ci.smd function from Kelley and Lai's MBESS package]3.7 Welch-féle d-próba
Azt teszteljük, hogy két független változó várható értékének különbsége (\(\mu_d=\mu_1-\mu_2\)) eltér-e egy adott értéktől (\(d_0\)). Továbbra is feltételezzük a normális eloszlást.
Alkalmazási feltételek:
- két véletlen független minta: \(X_1\) és \(X_2\)
- \(X_1\) és \(X_2\) normális eloszlású a populációban
Null- és ellenhipotézisek:
- Nullhipotézis:
- \(H_0: \mu_d=d_0\)
- ha \(d_0=0\), akkor \(H_0: \mu_1-\mu_2=0\) vagy \(H_0: \mu_1=\mu_2\) formában is írható
- Ellenhipotézis:
- \(H_1: \mu_d \neq d_0\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_d < d_0\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_d > d_0\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
- ha \(d_0=0\), akkor a fenti ellenhipotézisek:
- \(H_1: \mu_1\neq\mu_2\) (kétoldali ellenhipotézis) vagy
- \(H_1: \mu_1<\mu_2\) (egyoldali, kisebb (bal oldali) ellenhipotézis) vagy
- \(H_1: \mu_1>\mu_2\) (egyoldali, nagyobb (jobb oldali) ellenhipotézis)
Próbastatisztika:
\[T=\frac{(\bar{X_1}-\bar{X_2})-d_0}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \sim t(w), w=\frac{(s_1^2/n_1 + s_1^2/n_1)^2}{(s_1^2/n_1)^2/(n_1-1) + (s_2^2/n_2)^2/(n_2-1)}\]
3.7.1 Példa egyoldali (bal kisebb) ellenhipotézissel: teniszkönyök kialakulása
Amatőr sportolók körében a teniszkönyök kialakulásában a nem megfelelő sporteszközök használata is jelentős szerepet kaphat. 45 önként jelentkező segítségével a könyökre nehezedő erőt mérték a tenyeres ütések során, kétféle teniszütő esetében. A szokásosnál nagyobb ütőt használók körében a mintaátlag 25,2, a minta szórása 8,6 és a mintaelemszám 33. Hagyományos ütőt használók körében ezek az értékek rendre: 33,9, 17,4 és 12. Vizsgáljuk meg azt a hipotézist, hogy a nagyobb ütőt használók körében kisebb a könyökre nehezedő erő!
Forrás: (Ott and Longnecker 2008)
Feltételezzük a populációban a két ütő esetében mért erő normális eloszlását. A mintabeli szórások megadott értékei alapján arról is meggyőződhetünk, hogy a populációbeli szórások nem azonosak. A fentiek alapján a Welch-féle d-próba egyoldali (bal, kisebb) változatát hajtjuk végre a következő null és ellenhipotézissel:
- \(H_0: \mu_1=\mu_2\)
- \(H_1: \mu_1<\mu_2\)
A Welch-féle d-próba végrehajtása egyoldali (bal oldali, kisebb) ellenhipotézissel. A példában összesítő adatok szerepelnek, így a PASWR2 csomag tsum.test() függvényét használjuk. Mindkét minta esetén megadjuk a mintaátlagokat (mean.x= és mean.y=), mintabeli szórásokat (sd.x= és sd.y) és mintaelemszámokat(n.x= és n.y=). A populációbeli szórások eltérése miatt a var.equal=F argumentumot is megadjuk, valamint bal oldali ellenhipotézis miatt a alternative="less" paramétert is szerepeltetjük.
library(PASWR2)
PASWR2::tsum.test(mean.x = 25.2, s.x = 8.6, n.x = 33, mean.y = 33.9, s.y = 17.4, n.y = 12,
var.equal = F, alternative = "less")##
## Welch Two Sample t-test
##
## data: User input summarized values for x and y
## t = -1.6599, df = 13.006, p-value = 0.06042
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
## -Inf 0.5816739
## sample estimates:
## mean of x mean of y
## 25.2 33.9Az egyoldali (bal) Welch-féle d-próba eredményének értékelése. A egyoldali Welch-féle d-próba eredménye alapján azt mondhatjuk, hogy nincs elegendő bizonyítékunk arra, hogy a nagy méretű ütők kevésbé terhelik a könyököt (\(t(13,01)=-1,66, p=0,06\)).
A Welch-féle d-próba kézi számolása. A próba outputjában szereplő értékeket magunk is kiszámolhatjuk:
atlag <- 25.2 - 33.9 # a mintaátlagok különbsége
szoras.1 <- 8.6 # 1. adatminta szórása
szoras.2 <- 17.4 # 2. adatminta szórása
n.1 <- 33 # 1. minta elemszáma
n.2 <- 12 # 2. minta elemszáma
SE <- sqrt(szoras.1^2/n.1 + szoras.2^2/n.2) # standard hiba a különbségre
d.0 <- 0 # hipotetikus várható érték
t <- (atlag-d.0)/SE # próbastatisztika értéke
t # próbastatisztika értékének kiírása## [1] -1.659894df <- (szoras.1^2/n.1+szoras.2^2/n.2)^2/ # df
(((szoras.1^2/n.1)^2/(n.1-1))+((szoras.2^2/n.2)^2/(n.2-1)))
pt(q = t, df = df) # a p érték bal oldali próba esetén## [1] 0.06042046Konfidenciaintervallum kézi számolása kétmintás t-próbához. A próba outputjában szereplő konfidenciaintervallum határait kézi számolással is meghatározzuk. A várható értékre vonatkozó \(\left(1-\alpha \right)\) megbízhatóságú konfidenciaintervallum:
\[\left] (\bar{X_1}-\bar{X_2})-t_{\alpha, df}\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}, (\bar{X_1}-\bar{X_2})+t_{\alpha, df}\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} \right[\]
# A 95%-os konfidenciaintervallumra a kézi kiszámolási mód
atlag <- 25.2 - 33.9 # mintaátlagok különbsége
szoras.1 <- 8.6 # 1. adatminta szórása
szoras.2 <- 17.4 # 2. adatminta szórása
n.1 <- 33 # 1. minta elemszáma
n.2 <- 12 # 2. minta elemszáma
SE <- sqrt(szoras.1^2/n.1 + szoras.2^2/n.2) # standard hiba a különbségre
alfa <- 0.05 # alfa=1-0.95
df <- (szoras.1^2/n.1+szoras.2^2/n.2)^2/
(((szoras.1^2/n.1)^2/(n.1-1))+((szoras.2^2/n.2)^2/(n.2-1))) # df
t.alfa <- qt(p = 1-alfa, df = df) # t_{alfa,df} kritikusérték
atlag + c(-Inf, t.alfa*SE) # a 95%-os konf.intv. határai ## [1] -Inf 0.5816739A Welch-féle d-próba feltételeinek ellenőrzése. Minta hiányában nem tudjuk a normalitási feltételt ellenőrizni. Most a szórások eltérésére vonatkozó feltételezésünket ellenőrizzük F-próba segítségével.
# F-próba kézi végrehajtása
s.x.2 <- 8.6^2
s.y.2 <- 17.4^2
n.x <- 33
n.y <- 12
(F.stat <- s.x.2/s.y.2)## [1] 0.24428592 * (pf(F.stat, df1 = n.x - 1, df2 = n.y - 1))## [1] 0.001730069Az F-próba eredményéből kiolvasható, hogy a populációbeli szórások eltérnek (\(p=0,0017\)).
A hatás nagyságának meghatározása Welch-féle d-próbában. A Welch-féle d-próba esetén a hatás nagysága (effect size):
\[d=\left|\frac{(\bar{X_1}-\bar{X_2})-d_0}{\sqrt{(s_1^2+s_2^2)/2}}\right|\]
atlag <- 25.2 - 33.9 # mintaátlagok különbsége
szoras.1 <- 8.6 # 1. adatminta szórása
szoras.2 <- 17.4 # 2. adatminta szórása
s <- sqrt((szoras.1^2 + szoras.2^2)/2) # közös szórás
atlag / s # a Cohen-d értéke, előjelesen## [1] -0.6339061A Cohen-d értéke 0,63, ami azt mutatja, hogy a hatás közepes mértékű.
Az erő meghatározása Welch-féle d-próbában A statisztikai erő meghatározásához a powerAnalysis csomag power.t() függvényét használjuk. A bemenő paraméterek:
es=- a hatás nagyságan=- a összmintaelemszámtype=- az elemszámok különbözőségeratio=- az elemszámok aránya a két csoportbansig.level=- az \(\alpha\) szignifikanciaszintalternative=- az ellenhipotézis formája
A power.t() függvény a kétmintás t-próbánál használatos erő-számoló függvény, de visszatérési értéke nem sokban tér el a Welch-féle d-próbához tartozó erőtől
library(powerAnalysis)
power.t(es = -0.6339, n=45, sig.level=0.05, type="unequal", ratio=33/12, alternative="left")##
## Two-sample (unequal size) t test power calculation
##
## es = -0.6339
## power = 0.5815612
## n = 45
## n1 = 33
## n2 = 12
## ratio = 2.75
## sig.level = 0.05
## alternative = left
##
## NOTE: n is the total number of observationsAz output alapján azt mondhatjuk, hogy a próba statisztikai ereje 58%-os.
Mintaelemszám meghatározása Welch-féle d-próbában. Ha 80%-os statisztikai erőre van szükségünk a próba végrehajtása során, akkor ugyanilyen hatásnagyság kimutatásához (\(d=0.63\)), mekkora mintaelemszámra van szükség?
library(powerAnalysis)
power.t(es = -0.6339, power = 0.8, sig.level=0.05, type="unequal", ratio=33/12, alternative="left")##
## Two-sample (unequal size) t test power calculation
##
## es = -0.6339
## power = 0.8
## n = 80.06643
## n1 = 58.71538
## n2 = 21.35105
## ratio = 2.75
## sig.level = 0.05
## alternative = left
##
## NOTE: n is the total number of observationsLátható, hogy a 80%-os statisztikai erő eléréséhez (kerekítve) 80 elemű mintára van szükség, és ha meg akarjuk tartani az eredeti elemszámok arányát a két mintában, akkor 59 és 21 fős csoportokra van szükség.