6 Összefüggés két változó között
6.1 Korrelációs együtthatók
A korrelációszámítás két véletlen változó szimmetrikus kapcsolatával foglalkozik. Az \(X\) és \(Y\) változó között pozitív korrelációs kapcsolat van, ha kis \(X\) értékekhez kis \(Y\) értékek, nagy \(X\) értékekhez nagy \(Y\) értékek tartoznak. Negatív kapcsolat esetén kis \(X\) értékekhez nagy \(Y\) értékek, nagy \(X\) értékekhez kis \(Y\) értékek tartoznak. A két változó lineáris kapcsolatának erősségét a Pearson-féle korrelációs együtthatóval (populációban a \(\rho_{xy}\) vagy \(\rho\), a mintában \(r_{xy}\) vagy \(r\)) mérhetjük, nemlineáris, de monoton kapcsolat esetén a Spearman-féle rangkorrelációs együtthatót (\(\rho_S\), \(r_S\)), vagy a Kendall-féle tau-t (\(\tau\), \(r_{\tau}\)) használjuk. Mindhárom korrelációs mutatóhoz hipotézisvizsgálat társul, amelyek mindegyikében a nullhipotézisben a kapcsolat hiánya szerepel.
Alkalmazási feltételek:
- \(X\), \(Y\) véletlen változók
- Pearson-féle korrelációs együtthatóhoz kapcsolódó hipotézisvizsgálatban:
- lineáris kapcsolat feltételezhető a két változó között
- az \(X\) és \(Y\) változó kétdimenziós normális eloszlású a populációban, amelynek szükséges feltétele, hogy \(X\) és \(Y\) normális eloszlású legyen
- Spearman-féle rangkorrelációs együtthatóhoz és a Kendall-féle tau-hoz kapcsolódó hipotézisvizsgálatokban:
- legalább ordinális skála
- monoton kapcsolat feltételezhető a két változó között
Null- és ellenhipotézisek:
A Pearson-féle korrelációs együtthatóhoz:
- \(H_0:\) \(X\) és \(Y\) nincs lineáris kapcsolatban egymással
- \(H_1:\) \(X\) és \(Y\) lineáris kapcsolatban van egymással
vagyis
- \(H_0:\rho = 0\)
- \(H_1:\rho \neq 0\)
A Spearman-féle rangkorrelációs együtthatóhoz és a Kendall-féle tau-hoz:
- \(H_0:\) \(X\) és \(Y\) nincs monoton kapcsolatban egymással
- \(H_1:\) \(X\) és \(Y\) monoton kapcsolatban van egymással
azaz Spearman-féle rangkorrelációs együttható esetén:
- \(H_0:\rho_{S}=0\)
- \(H_1:\rho_{S} \neq 0\)
Kendall-féle tau esetén:
- \(H_0:\tau = 0\)
- \(H_1:\tau \neq 0\)
Próbastatisztika:
A Pearson-féle korrelációs együttható (\(r\)) értelmezhető a standardizált kovarianciaként: a kovariancia (\(\sigma_{xy}\)) per a két változó szórása (\(\sigma_x\) és \(\sigma_y\)). Az \(r\)-re épülő próbastatisztika \(t(n-2)\) eloszlású, ha \(H_0\) igaz.
\[r=r_{xy}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^n(y_i-\bar{y})^2}}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{(n-1) s_x s_y}=\frac{s_{xy}}{s_x s_y}\]
\[T=r\sqrt{\frac{n-2}{1-r^2}} \sim t(n-2)\]
Spearman-féle rangkorrelációs együttható definíció szerint a rangokon kiszámolt Pearson-féle korrelációs együtthatóval egyenlő. Ha kapcsolt rangokat nem tartalmaz a két változó, akkor számolhatunk a következő közelítő képlettel is. Az \(r_S\)-re épülő próbastatisztika szintén \(t(n-2)\) eloszlású, ha \(H_0\) igaz.
\[r_i=\text{rank}(x_i), q_i=\text{rank}(y_i), d_i=\left|r_i-q_i\right|, r_S=1-\frac{6\sum_{i=1}^nd_i^2}{n^3-n}, T=r_S\sqrt{\frac{n-2}{1-r_S^2}} \sim t(n-2)\]
Kendall-féle tau mutató a konkordáns és diszkordáns párok számát veszi figyelembe. Konkordánsnak nevezünk egy \((x_i, y_i)\) és \((x_j, y_j)\) párt, ha \(x_i<x_j\) esetén \(y_i<y_j\) vagy \(x_i>x_j\) esetén \(y_i>y_j\). Diszkordánsnak nevezünk egy \((x_i, y_i)\) és \((x_j, y_j)\) párt, ha \(x_i<x_j\) esetén \(y_i>y_j\) vagy \(x_i>x_j\) esetén \(y_i<y_j\). Ha \(n_C\)-vel jelöljük a konkordáns párok számát, és \(n_D\)-vel a diszkordáns párok számát, valamint ha figyelembe vesszük, hogy \(n\) elemű minta esetén összesen \(n(n-1)/2\) számú pár képezhető, akkor \(n_C+n_D = n(n-1)/2\) (feltéve, hogy nincsenek kapcsolt rangok). Ekkor a mutató számítása:
\[r_{\tau}=\frac{n_C-n_D}{n_C+n_D}=\frac{n_C-n_D}{n(n-1)/2}\]
Kapcsolt rangok esetén egy némileg módosított képlettel kell számolni. Az \(r_{\tau}\)-ra épülő próbastatisztika a nullhipotézis igaz volta esetén, ha \(n\) elég nagy, akkor közelítőleg standard normális eloszlást követ:
\[Z=\frac{r_{\tau}}{\sigma_{\tau}}=\frac{r_{\tau}}{\sqrt{\frac{2(2n+5)}{9n(n-1)}}} \sim N(0,1)\]
Kapcsolt rangok hiányában a próbastatisztika értéke pontosan is számolható, egzakt értéket is kaphatunk.
6.1.1 Példa: hőmérséklet és az elfogyasztott jégkrémek száma
Vizsgáljuk meg a hőmérséklet és az elfogyasztott jégkrémek száma közötti kapcsolatot!
Forrás: (Dancey and Reidy 2011, 181)
Adatok beolvasása. Olvassuk be az adatokat egy d nevű adattáblába:
d <- read.table(file = textConnection("
Ice.cream Temperature
1000 26
950 22
870 19
890 20
886 19
900 21
560 17
550 16
400 12
500 13
550 14
600 19
700 21
750 22
800 22
850 24
950 22
1050 26
1000 26
1000 26
"), header=T, sep="")
str(d) # az adattábla szerkezete## 'data.frame': 20 obs. of 2 variables:
## $ Ice.cream : int 1000 950 870 890 886 900 560 550 400 500 ...
## $ Temperature: int 26 22 19 20 19 21 17 16 12 13 ...d # a beolvasott adattábla## Ice.cream Temperature
## 1 1000 26
## 2 950 22
## 3 870 19
## 4 890 20
## 5 886 19
## 6 900 21
## 7 560 17
## 8 550 16
## 9 400 12
## 10 500 13
## 11 550 14
## 12 600 19
## 13 700 21
## 14 750 22
## 15 800 22
## 16 850 24
## 17 950 22
## 18 1050 26
## 19 1000 26
## 20 1000 26Grafikus ábrázolás két kvantitatív változó kapcsolatára. Kétdimenziós pontdiagram segítségével ábrázoljuk a két változó kapcsolatát:
library(ggplot2)
ggplot(data = d, mapping = aes(x = Temperature, y = Ice.cream)) + geom_point(size=4, colour = "blue", alpha = 0.6, shape=21, fill="grey") + theme_bw()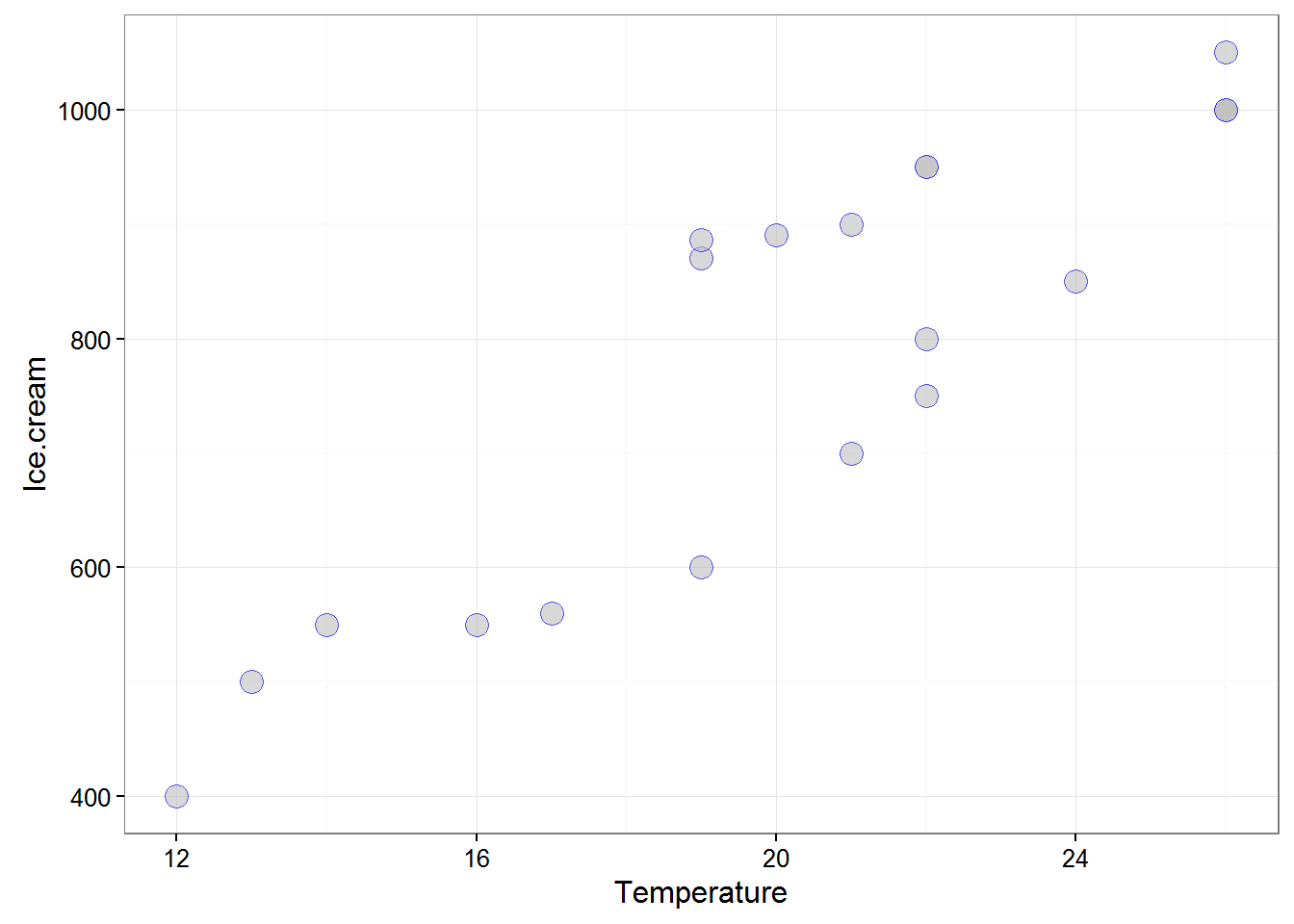
Korrelációs együtthatók kiszámítása. A három korrelációs együttható meghatározható a DescTools csomag Desc() függvényével. Argumentumként a két változót tartalmazó formula=Ice.cream~Temperature argumentumot kell megadni.
library(DescTools)
Desc(formula = Ice.cream ~ Temperature, data = d)## -------------------------------------------------------------------------
## Ice.cream ~ Temperature
##
## Summary:
## n pairs: 20, valid: 20 (100.0%), missings: 0 (0.0%)
##
##
## Pearson corr. : 0.8930702
## Spearman corr.: 0.8627080
## Kendall corr. : 0.7747370Mindhárom együttható erős pozitív kapcsolatot jelez a két változó között.
A Pearson-féle korrelációs együttható magas értéke erős pozitív lineáris kapcsolatot jelent (\(r=0,89\)). A Pearson-féle korrelációs együttható értemezését segíti az a tény, hogy az erre épülő determinációs együttható (\(r^2=0,80\)) értéke alapján azt mondhatjuk, hogy a hőmérséklet ismeretében az elfogyasztott jégkrémek számára vonatkozó előrejelzésünk hibája 80%-kal csökkenthető (lineáris regresszió esetén). A másik értelmezés is a lineáris regresszióhoz kötődik. Az elfogyasztott jégrém mennyiségében 0,89 szeres saját szórásban mért növekedés következik be egy saját szórásnyi hőmérsékletben bekövetkező növekedés esetén.
A Spearman-féle rangkorrelációs együttható magas értéke erős pozitív monoton kapcsolatot jelent (\(r_S=0,86\)). (Értelmezése nem egyszerű, mivel a rangokon végrehajtott Pearson-féle korrelációs együtthatót szolgáltatja.)
A Kendall-féle tau együttható magas értéke erős pozitív monoton kapcsolatot jelent (\(r_{\tau}=0,77\)). A mutató értelmezése szerint a hőmérsékletek értékei közötti nagyságrendi viszony, kb. 77%-os mértékben jelenik meg az elfogyasztott jégkrémek száma változó értékeiben. A konkordáns párok aránya is kiszámolható \(r_{\tau}\) ismeretében: \((1+r_{\tau})/2=0,89\). Tehát a mintában a 89%-11% a konkordáns-diszkordáns párok aránya.
Hipotézisvizsgálat a Pearson-féle korrelációs együtthatóra, a Spearman-féle rangkorrelációs együtthatóra és a Kendall-féle tau együtthatóra. A próbák végrehajtása.
# hipotézisvizsgálat a Pearson-féle korrelációs együtthatóra
cor.test(d$Ice.cream, d$Temperature, method = "pearson", use="complete.obs")##
## Pearson's product-moment correlation
##
## data: d$Ice.cream and d$Temperature
## t = 8.4215, df = 18, p-value = 0.0000001171
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7449587 0.9572742
## sample estimates:
## cor
## 0.8930702# hipotézisvizsgálat a Spearman-féle rangkorrelációs együtthatóra
cor.test(d$Ice.cream, d$Temperature, method = "spearman", use="complete.obs") ##
## Spearman's rank correlation rho
##
## data: d$Ice.cream and d$Temperature
## S = 182.6, p-value = 0.0000009893
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.862708# hipotézisvizsgálat a Kendall-féle tau együtthatóra
cor.test(d$Ice.cream, d$Temperature, method = "kendall", use="complete.obs")##
## Kendall's rank correlation tau
##
## data: d$Ice.cream and d$Temperature
## z = 4.5758, p-value = 0.000004743
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
## tau
## 0.774737A fenti három próba outputjából kiderül, hogy az adott együtthatóra vonatkozó nullhipotézist visszautasítjuk, tehát a három együttható értéke szignifikánsan eltér nullától, ami a lineráis/monoton korrelációs kapcsolat jelenlétét bizonyítja a populációban (Pearson-féle korrelációs együtthatóra: \(r=0,89\); \(t(18)=8,4215\); \(p<0,0001\); Spearman-féle rangkorrelációs együtthatóra: \(r_S=0,86\); \(p<0,0001\); Kendall-féle tau együtthatóra: \(r_{\tau}=0,77\); \(z=4,5758\); \(p<0,0001\)).
Alternatívák a korrelációs együtthatókra. A lessR csomag Correlation() függvényével is elvégezhetjük a fenti hipotézisvizsgálatokat:
library(lessR)
# hipotézisvizsgálat a Pearson-féle korrelációs együtthatóra
Correlation(Ice.cream, Temperature, data = d, method = "pearson")## Correlation Analysis for Variables Ice.cream and Temperature
## ------------------------------------------------------------
##
## >>> Pearson's product-moment correlation
##
## Number of paired values with neither missing, n = 20
## Number of cases (rows of data) deleted: 0
##
##
## Sample Covariance: s = 760.495
##
## Sample Correlation: r = 0.893
##
##
## Alternative Hypothesis: True correlation is not equal to 0
## t-value: 8.421, df: 18, p-value: 0.000
##
## 95% Confidence Interval of Population Correlation
## Lower Bound: 0.745 Upper Bound: 0.957# hipotézisvizsgálat a Spearman-féle rangkorrelációs együtthatóra
Correlation(Ice.cream, Temperature, data = d, method = "spearman")## Correlation Analysis for Variables Ice.cream and Temperature
## ------------------------------------------------------------
##
## >>> Spearman's rank correlation rho
##
## Number of paired values with neither missing, n = 20
## Number of cases (rows of data) deleted: 0
##
##
## Sample Correlation: rho = 0.863
##
##
## Alternative Hypothesis: True rho is not equal to 0
## S-value: 182.598, p-value: 0.000# hipotézisvizsgálat a Kendall-féle tau együtthatóra
Correlation(Ice.cream, Temperature, data = d, method = "kendall") ## Correlation Analysis for Variables Ice.cream and Temperature
## ------------------------------------------------------------
##
## >>> Kendall's rank correlation tau
##
## Number of paired values with neither missing, n = 20
## Number of cases (rows of data) deleted: 0
##
##
## Sample Correlation: tau = 0.775
##
##
## Alternative Hypothesis: True tau is not equal to 0
## z-value: 4.576, p-value: 0.000A DescTools csomag Assocs() függvényével egyéb asszociációs mutatókat is meghatározhatunk:
library(DescTools)
Assocs(table(d$Ice.cream, d$Temperature))## estimate lwr.ci upr.ci
## Phi Coeff. 3.0000 - -
## Contingency Coeff. 0.9487 - -
## Cramer V 0.9487 0.0000 0.6152
## Goodman Kruskal Gamma 0.8035 0.6042 1.0000
## Kendall Tau-b 0.7747 0.5779 0.9716
## Stuart Tau-c 0.7645 0.5717 0.9573
## Somers D C|R 0.7514 0.5510 0.9517
## Somers D R|C 0.7989 0.5890 1.0000
## Pearson Correlation 0.8488 0.6506 0.9387
## Spearman Correlation 0.8627 0.6797 0.9446
## Lambda C|R 0.9375 0.8189 1.0000
## Lambda R|C 0.6471 0.4199 0.8742
## Lambda sym 0.7879 0.6610 0.9148
## Uncertainty Coeff. C|R 0.9064 0.7386 1.0000
## Uncertainty Coeff. R|C 0.7448 0.5940 0.8956
## Uncertainty Coeff. sym 0.8177 0.6655 0.9699
## Mutual Information 3.0842 - -6.2 Parciális korrelációs együtthatók
6.2.1 Példa: a vizsgaeredmények, a felkészülési idő és a szorongás kapcsolata
Egy vizsgálatban rendelkezésre áll 103 tanuló vizsgaeredménye (
Exam), a felkészülésre fordított idő (Revise) és a vizsgával kapcsolatos szorongás mértéke (Anxiety). Vizsgáljuk meg a három változó kapcsolatát!
Forrás: (A. Field, Miles, and Field 2012, 219)
Adatok beolvasása. Olvassuk be az adatokat egy d adattáblába!
d <- read.table(file = textConnection("
Code Revise Exam Anxiety Gender
1 4 40 86.298 Male
2 11 65 88.716 Female
3 27 80 70.178 Male
4 53 80 61.312 Male
5 4 40 89.522 Male
6 22 70 60.506 Female
7 16 20 81.462 Female
8 21 55 75.82 Female
9 25 50 69.372 Female
10 18 40 82.268 Female
11 18 45 79.044 Male
12 16 85 80.656 Male
13 13 70 70.178 Male
14 18 50 75.014 Female
15 98 95 34.714 Male
16 1 70 95.164 Male
17 14 95 75.82 Male
18 29 95 79.044 Female
19 4 50 91.134 Female
20 23 60 64.536 Male
21 14 80 80.656 Male
22 12 75 77.432 Male
23 22 85 65.342 Female
24 84 90 .0560000000000116 Female
25 23 30 71.79 Female
26 26 60 81.462 Female
27 24 75 63.73 Male
28 72 75 27.46 Female
29 37 27 73.402 Female
30 10 20 89.522 Male
31 3 75 89.522 Female
32 36 90 75.014 Female
33 43 60 43.58 Male
34 19 30 82.268 Male
35 12 80 79.044 Male
36 9 10 79.044 Female
37 72 85 37.132 Male
38 10 7 81.462 Male
39 12 5 83.074 Female
40 30 85 50.834 Male
41 15 20 82.268 Male
42 8 45 78.238 Female
43 34 60 72.596 Male
44 22 70 74.208 Female
45 21 50 75.82 Female
46 27 25 70.984 Male
47 6 50 97.582 Male
48 18 40 67.76 Male
49 8 80 75.014 Male
50 19 50 73.402 Female
51 0 35 93.552 Female
52 52 80 58.894 Female
53 38 50 53.252 Female
54 19 49 84.686 Male
55 23 75 89.522 Female
56 11 25 71.79 Female
57 27 65 82.268 Male
58 17 80 69.372 Male
59 13 50 62.118 Male
60 42 70 68.566 Female
61 4 40 93.552 Male
62 8 80 84.686 Female
63 6 10 82.268 Male
64 11 20 81.462 Female
65 7 40 82.268 Male
66 15 40 91.134 Male
67 4 70 91.94 Female
68 28 52 86.298 Female
69 22 50 72.596 Male
70 29 60 63.73 Female
71 2 80 63.73 Male
72 16 60 71.79 Female
73 59 65 57.282 Male
74 10 15 84.686 Female
75 13 85 84.686 Male
76 8 20 77.432 Female
77 5 80 82.268 Female
78 2 100 10 Male
79 38 100 50.834 Female
80 4 80 87.91 Male
81 10 10 83.88 Male
82 6 70 84.686 Female
83 68 100 20.206 Female
84 8 70 87.104 Male
85 1 70 83.88 Female
86 14 65 67.76 Male
87 42 75 95.97 Female
88 13 85 62.118 Female
89 1 30 84.686 Male
90 3 5 92.746 Male
91 5 10 84.686 Female
92 12 90 83.074 Female
93 19 70 73.402 Male
94 2 20 87.91 Female
95 19 85 71.79 Male
96 11 35 86.298 Male
97 15 30 84.686 Female
98 23 70 75.82 Male
99 13 55 70.984 Female
100 14 75 78.238 Female
101 1 2 82.268 Male
102 9 40 79.044 Male
103 20 50 91.134 Female
"), header=T, sep="", dec = ".")
str(d) # az adattábla szerkezete## 'data.frame': 103 obs. of 5 variables:
## $ Code : int 1 2 3 4 5 6 7 8 9 10 ...
## $ Revise : int 4 11 27 53 4 22 16 21 25 18 ...
## $ Exam : int 40 65 80 80 40 70 20 55 50 40 ...
## $ Anxiety: num 86.3 88.7 70.2 61.3 89.5 ...
## $ Gender : Factor w/ 2 levels "Female","Male": 2 1 2 2 2 1 1 1 1 1 ...d # a beolvasott adattábla## Code Revise Exam Anxiety Gender
## 1 1 4 40 86.298 Male
## 2 2 11 65 88.716 Female
## 3 3 27 80 70.178 Male
## 4 4 53 80 61.312 Male
## 5 5 4 40 89.522 Male
## 6 6 22 70 60.506 Female
## 7 7 16 20 81.462 Female
## 8 8 21 55 75.820 Female
## 9 9 25 50 69.372 Female
## 10 10 18 40 82.268 Female
## 11 11 18 45 79.044 Male
## 12 12 16 85 80.656 Male
## 13 13 13 70 70.178 Male
## 14 14 18 50 75.014 Female
## 15 15 98 95 34.714 Male
## 16 16 1 70 95.164 Male
## 17 17 14 95 75.820 Male
## 18 18 29 95 79.044 Female
## 19 19 4 50 91.134 Female
## 20 20 23 60 64.536 Male
## 21 21 14 80 80.656 Male
## 22 22 12 75 77.432 Male
## 23 23 22 85 65.342 Female
## 24 24 84 90 0.056 Female
## 25 25 23 30 71.790 Female
## 26 26 26 60 81.462 Female
## 27 27 24 75 63.730 Male
## 28 28 72 75 27.460 Female
## 29 29 37 27 73.402 Female
## 30 30 10 20 89.522 Male
## 31 31 3 75 89.522 Female
## 32 32 36 90 75.014 Female
## 33 33 43 60 43.580 Male
## 34 34 19 30 82.268 Male
## 35 35 12 80 79.044 Male
## 36 36 9 10 79.044 Female
## 37 37 72 85 37.132 Male
## 38 38 10 7 81.462 Male
## 39 39 12 5 83.074 Female
## 40 40 30 85 50.834 Male
## 41 41 15 20 82.268 Male
## 42 42 8 45 78.238 Female
## 43 43 34 60 72.596 Male
## 44 44 22 70 74.208 Female
## 45 45 21 50 75.820 Female
## 46 46 27 25 70.984 Male
## 47 47 6 50 97.582 Male
## 48 48 18 40 67.760 Male
## 49 49 8 80 75.014 Male
## 50 50 19 50 73.402 Female
## 51 51 0 35 93.552 Female
## 52 52 52 80 58.894 Female
## 53 53 38 50 53.252 Female
## 54 54 19 49 84.686 Male
## 55 55 23 75 89.522 Female
## 56 56 11 25 71.790 Female
## 57 57 27 65 82.268 Male
## 58 58 17 80 69.372 Male
## 59 59 13 50 62.118 Male
## 60 60 42 70 68.566 Female
## 61 61 4 40 93.552 Male
## 62 62 8 80 84.686 Female
## 63 63 6 10 82.268 Male
## 64 64 11 20 81.462 Female
## 65 65 7 40 82.268 Male
## 66 66 15 40 91.134 Male
## 67 67 4 70 91.940 Female
## 68 68 28 52 86.298 Female
## 69 69 22 50 72.596 Male
## 70 70 29 60 63.730 Female
## 71 71 2 80 63.730 Male
## 72 72 16 60 71.790 Female
## 73 73 59 65 57.282 Male
## 74 74 10 15 84.686 Female
## 75 75 13 85 84.686 Male
## 76 76 8 20 77.432 Female
## 77 77 5 80 82.268 Female
## 78 78 2 100 10.000 Male
## 79 79 38 100 50.834 Female
## 80 80 4 80 87.910 Male
## 81 81 10 10 83.880 Male
## 82 82 6 70 84.686 Female
## 83 83 68 100 20.206 Female
## 84 84 8 70 87.104 Male
## 85 85 1 70 83.880 Female
## 86 86 14 65 67.760 Male
## 87 87 42 75 95.970 Female
## 88 88 13 85 62.118 Female
## 89 89 1 30 84.686 Male
## 90 90 3 5 92.746 Male
## 91 91 5 10 84.686 Female
## 92 92 12 90 83.074 Female
## 93 93 19 70 73.402 Male
## 94 94 2 20 87.910 Female
## 95 95 19 85 71.790 Male
## 96 96 11 35 86.298 Male
## 97 97 15 30 84.686 Female
## 98 98 23 70 75.820 Male
## 99 99 13 55 70.984 Female
## 100 100 14 75 78.238 Female
## 101 101 1 2 82.268 Male
## 102 102 9 40 79.044 Male
## 103 103 20 50 91.134 FemalePearson-féle korrelációs együtthatók meghatározása. A változók páronkénti kapcsolatát tárjuk fel a Pearson-féle korrelációs együttható segítségével. A cor() függvény alkalmas az ún. korrelációs mátrixot meghatározására, amely a páronként vett korrelációs együtthatókat szolgáltatja. A korrelációs mátrix grafikus szemléltetésére a corrplot csomag corrplot() függvényét használjuk. Az lsr csomag correlate() függvényével a hipotézisvizsgálatokat is elvégezhetjük.
korr <- cor(d[, c("Revise", "Exam", "Anxiety")], method = "pearson", use = "complete.obs")
korr## Revise Exam Anxiety
## Revise 1.0000000 0.3967207 -0.7092493
## Exam 0.3967207 1.0000000 -0.4409934
## Anxiety -0.7092493 -0.4409934 1.0000000library(corrplot)
corrplot(korr, type="upper", tl.col="black", tl.srt=45, addCoef.col = "black", method = "ellipse")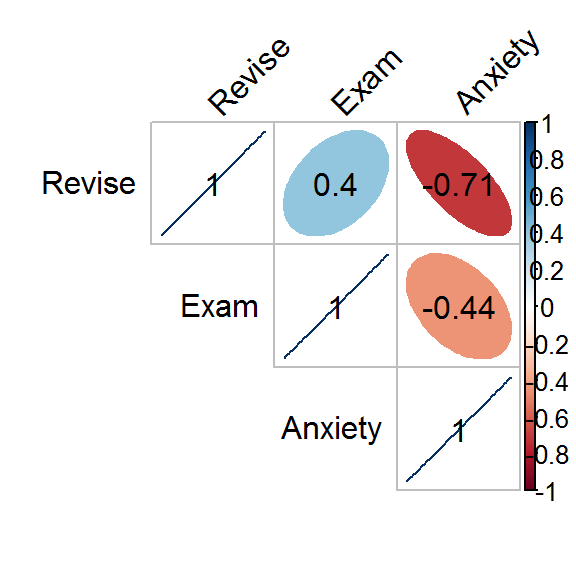
library(lsr)
correlate(d[, c("Revise", "Exam", "Anxiety")], test = T, corr.method = "pearson")##
## CORRELATIONS
## ============
## - correlation type: pearson
## - correlations shown only when both variables are numeric
##
## Revise Exam Anxiety
## Revise . 0.397 -0.709
## Exam 0.397 . -0.441
## Anxiety -0.709 -0.441 .
##
##
## p-VALUES
## ========
## - total number of tests run: 3
## - correction for multiple testing: holm
##
## Revise Exam Anxiety
## Revise . 0.000 0.000
## Exam 0.000 . 0.000
## Anxiety 0.000 0.000 .
##
##
## SAMPLE SIZES
## ============
##
## Revise Exam Anxiety
## Revise 103 103 103
## Exam 103 103 103
## Anxiety 103 103 103A fenti outputból kiolvasható, hogy a vizsgával kapcsolatos szorongás növekedésével, csökken a vizsgán nyújtott teljesítmény (\(r=-0,441\); \(p<0,0001\)). A felkészülésre fordított idő növekedésével, a vizsgány nyújtott teljesítmény is nő (\(r=0,397\); \(p<0,0001\)). A felküszlésre fordított idő növekedésével, a vizsgával kapcsolatos szorongás csökken (\(r=-0,709\); \(p<0,0001\)).
Parciális Pearson-féle korrelációs együtthatók meghatározása. A parciális korrelációs együtthatókat a corpcor csomag cor2pcor() függvényével is meghatározhatjuk. Argumentumként a korrelációs együtthatót kell megadni. A grafikus ábrázolást most is a corplot() függvénnyel végezzük el. A parciális korrelációs együtthatókra vonatkozó hipotézisvizsgálatokat az Rcmdr csomag partial.cor() függvényével hajthatjuk végre.
korr <- cor(d[,c("Revise", "Exam", "Anxiety")], method = "pearson", use = "complete.obs")
library(corpcor)
p.korr <- cor2pcor(m = korr)
p.korr## [,1] [,2] [,3]
## [1,] 1.0000000 0.1326783 -0.6485301
## [2,] 0.1326783 1.0000000 -0.2466658
## [3,] -0.6485301 -0.2466658 1.0000000library(corrplot)
corrplot(p.korr, type="upper", tl.col="black", tl.srt=45, addCoef.col = "black", method = "ellipse")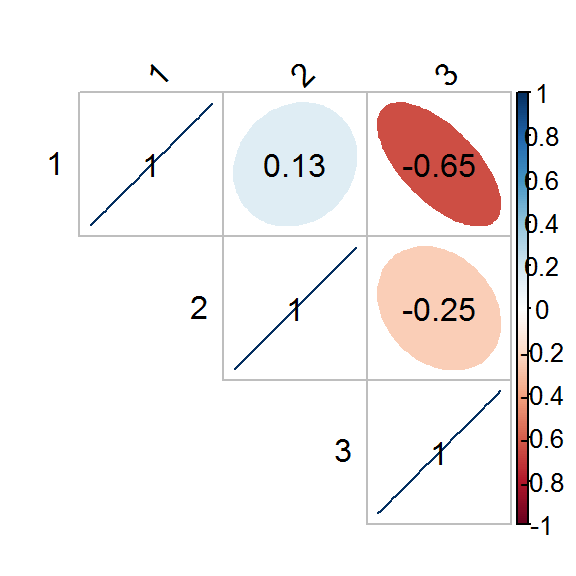
library(Rcmdr)
partial.cor(d[,c("Revise", "Exam", "Anxiety")], use="complete.obs", test=T)##
## Partial correlations:
## Revise Exam Anxiety
## Revise 0.00000 0.13268 -0.64853
## Exam 0.13268 0.00000 -0.24667
## Anxiety -0.64853 -0.24667 0.00000
##
## Number of observations: 103
##
## Pairwise two-sided p-values:
## Revise Exam Anxiety
## Revise 0.1837 <.0001
## Exam 0.1837 0.0124
## Anxiety <.0001 0.0124
##
## Adjusted p-values (Holm's method)
## Revise Exam Anxiety
## Revise 0.1837 <.0001
## Exam 0.1837 0.0249
## Anxiety <.0001 0.0249A parciális korrelációs együtthatók két változó kapcsolatának erősségét méri, miközben figyelembe veszünk egy harmadik változót is.
6.3 Korrelációs együtthatók összehasonlítása
6.3.1 Példa: a szorongás és a vizsgán nyújtott teljesítmény férfiak és nők körében
library(cocor)
cocor.indep.groups(r1.jk = -.506, r2.hm = -0.381, n1 = 52, n2 = 51)##
## Results of a comparison of two correlations based on independent groups
##
## Comparison between r1.jk = -0.506 and r2.hm = -0.381
## Difference: r1.jk - r2.hm = -0.125
## Group sizes: n1 = 52, n2 = 51
## Null hypothesis: r1.jk is equal to r2.hm
## Alternative hypothesis: r1.jk is not equal to r2.hm (two-sided)
## Alpha: 0.05
##
## fisher1925: Fisher's z (1925)
## z = -0.7687, p-value = 0.4421
## Null hypothesis retained
##
## zou2007: Zou's (2007) confidence interval
## 95% confidence interval for r1.jk - r2.hm: -0.4430 0.1927
## Null hypothesis retained (Interval includes 0)cocor.dep.groups.overlap(r.jk = -0.441, r.jh = 0.397, r.kh = -0.709, n = 103)##
## Results of a comparison of two overlapping correlations based on dependent groups
##
## Comparison between r.jk = -0.441 and r.jh = 0.397
## Difference: r.jk - r.jh = -0.838
## Related correlation: r.kh = -0.709
## Group size: n = 103
## Null hypothesis: r.jk is equal to r.jh
## Alternative hypothesis: r.jk is not equal to r.jh (two-sided)
## Alpha: 0.05
##
## pearson1898: Pearson and Filon's z (1898)
## z = -5.6676, p-value = 0.0000
## Null hypothesis rejected
##
## hotelling1940: Hotelling's t (1940)
## t = -5.0958, df = 100, p-value = 0.0000
## Null hypothesis rejected
##
## williams1959: Williams' t (1959)
## t = -5.0881, df = 100, p-value = 0.0000
## Null hypothesis rejected
##
## olkin1967: Olkin's z (1967)
## z = -5.6676, p-value = 0.0000
## Null hypothesis rejected
##
## dunn1969: Dunn and Clark's z (1969)
## z = -4.9066, p-value = 0.0000
## Null hypothesis rejected
##
## hendrickson1970: Hendrickson, Stanley, and Hills' (1970) modification of Williams' t (1959)
## t = -5.0682, df = 100, p-value = 0.0000
## Null hypothesis rejected
##
## steiger1980: Steiger's (1980) modification of Dunn and Clark's z (1969) using average correlations
## z = -4.8330, p-value = 0.0000
## Null hypothesis rejected
##
## meng1992: Meng, Rosenthal, and Rubin's z (1992)
## z = -4.8332, p-value = 0.0000
## Null hypothesis rejected
## 95% confidence interval for r.jk - r.jh: -1.2559 -0.5312
## Null hypothesis rejected (Interval does not include 0)
##
## hittner2003: Hittner, May, and Silver's (2003) modification of Dunn and Clark's z (1969) using a backtransformed average Fisher's (1921) Z procedure
## z = -4.8330, p-value = 0.0000
## Null hypothesis rejected
##
## zou2007: Zou's (2007) confidence interval
## 95% confidence interval for r.jk - r.jh: -1.1067 -0.5220
## Null hypothesis rejected (Interval does not include 0)6.4 Asszociációs mértékek
- Somers-féle monotonitási együtthatók
- Kendall-féle tau-b monotonitási együttható
- Goodman–Kruskal-féle gamma
- Kontingencia-együttható
- Cramer-féle \(V\)
- Phi kontingencia együttható
- Yule-féle Q
- Yule-féle Y
- Goodman–Kruskal-féle lambda (\(\lambda\))
- Közös információhányad
m <- matrix(c(5, 9, 7, 1, 4, 8, 11, 15, 3, 7, 22, 8), ncol = 4, byrow = T)
dimnames(m) <- list(Hajszin=c("Szőke", "Barna", "Fekete"), Szemszin=c("Kék", "Zöld", "Barna", "Fekete"))
m## Szemszin
## Hajszin Kék Zöld Barna Fekete
## Szőke 5 9 7 1
## Barna 4 8 11 15
## Fekete 3 7 22 8library(DescTools)
Assocs(m)## estimate lwr.ci upr.ci
## Phi Coeff. 0.4198 - -
## Contingency Coeff. 0.3871 - -
## Cramer V 0.2968 0.0845 0.3989
## Goodman Kruskal Gamma 0.2561 0.0389 0.4733
## Kendall Tau-b 0.1799 0.0245 0.3353
## Stuart Tau-c 0.1830 0.0229 0.3431
## Somers D C|R 0.1885 0.0268 0.3502
## Somers D R|C 0.1717 0.0259 0.3175
## Pearson Correlation 0.2379 0.0435 0.4149
## Spearman Correlation 0.2158 0.0203 0.3955
## Lambda C|R 0.1000 0.0000 0.3008
## Lambda R|C 0.1833 0.0000 0.3857
## Lambda sym 0.1417 0.0000 0.3215
## Uncertainty Coeff. C|R 0.0688 0.0092 0.1284
## Uncertainty Coeff. R|C 0.0842 0.0116 0.1568
## Uncertainty Coeff. sym 0.0757 0.0103 0.1412
## Mutual Information 0.1297 - -library(vcd)
assocstats(x = m)## X^2 df P(> X^2)
## Likelihood Ratio 17.975 6 0.0062947
## Pearson 17.622 6 0.0072499
##
## Phi-Coefficient : NA
## Contingency Coeff.: 0.387
## Cramer's V : 0.297