|
6.5.4 probléma: Többdimenziós skálázás összevetése a klaszteranalízis és a faktoranalízis eredményeivel.
Az utolsó példában egy már a faktoranalízis fejezetében megismert példát veszünk ismét elő. A 3.4.1 fejezetben található 3.1 R-forráskóddal hívhatjuk elő az adatokat, melyek magyarázata a 3.2 fejezetben található.
Az elemzés előtt most is a távolságmátrixot fogjuk elkészíteni a korrelációs mátrix alapján a 6.43. és 6.44. R-forráskód segítségével. A távolságmátrix a 6.44. R-eredményen látható.
cor<-cor(d)
d2<-matrix(0,nrow=6,ncol=6)
for(i in 1:6) for (j in 1:6)d2[i,j]<-sqrt(cor[i,i]-2*cor[i,j]+cor[j,j])
név=c("v1","v2","v3","v4","v5","v6")
rownames(d2)<-név
print(d2,digits=3)
|
| |
6.43. R-forráskód
|
[,1] [,2] [,3] [,4] [,5] [,6]
v1 0.000 0.757 0.758 0.963 0.992 1.77
v2 0.757 0.000 0.296 1.130 1.091 1.65
v3 0.758 0.296 0.000 1.128 1.057 1.67
v4 0.963 1.130 1.128 0.000 0.237 1.99
v5 0.992 1.091 1.057 0.237 0.000 1.99
v6 1.765 1.648 1.668 1.990 1.991 0.00
|
| |
6.43. R-eredmény.
|
dist<-as.dist(d2)
print(dist,digits=3)
|
| |
6.44. R-forráskód
|
v1 v2 v3 v4 v5
v2 0.757
v3 0.758 0.296
v4 0.963 1.130 1.128
v5 0.992 1.091 1.057 0.237
v6 1.765 1.648 1.668 1.990 1.991
|
| |
6.44. R-eredmény.
|
library(MASS)
mds<-isoMDS(dist)
|
| |
6.45. R-forráskód
|
A többdimenziós skálázást a 6.45. R-forráskód segítségével futtathatjuk.
plot(mds$points)
text(mds$points,labels=rownames(d2))
|
| |
6.46. R-forráskód
|
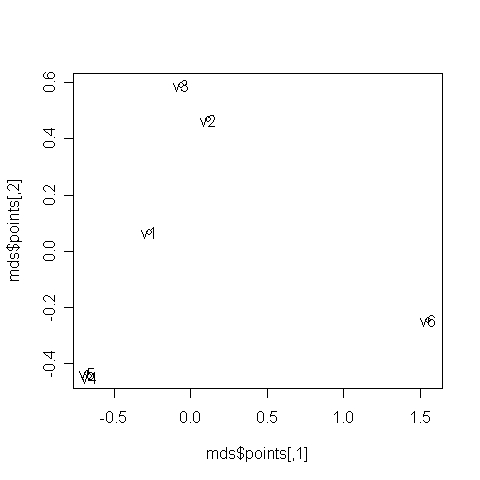
A 6.46. R-eredményen látható a kétdimenziós reprezentációja az adatoknak. Az ábra alapján a v4 és v5 viszonylag közel esik, hasonlít egymáshoz (vonás-szorongás itemei). A v6 távolabb esik a többi változótól (ez volt a fordított item), és a v1-v3, az állapot-szorongás itemei is viszonylag közel vannak egymáshoz.
Mielőtt a kapott eredményt összevetnénk a faktoranalízis és a klaszteranalízis eredményeivel, nézzük meg az illeszkedésmutatókat.
|
print(mds$stress,digits=3)
|
| |
6.47. R-forráskód
|
Első lépésben a Stess-értéket nézhetjük meg a 6.47. R-eredményen. Az értéke megfelelően kicsi, így elfogadhatjuk a kétdimenziós megoldást.
delta<-dist(mds$points)
plot(delta,dist)
|
| |
6.48. R-forráskód
|
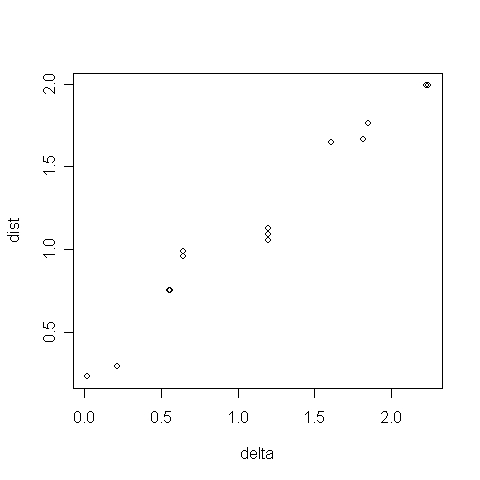
A Shepard-diagramon (6.48. R-eredmény) egy egyenesre illeszkednek az adatok, ami szintén a kétdimenziós megoldás jóságát erősíti meg.
Sh<-Shepard(dist,mds$points)
lm<-summary(lm(Sh$yf~Sh$x))
print(lm$r.squared,digits=3)
|
| |
6.49. R-forráskód
|
fi<-mds$stress^2/2
print(fi,digits=3)
|
| |
6.50. R-forráskód
|
mu<-cor(dist,delta)
print(mu,digits=4)
|
| |
6.51. R-forráskód
|
Az illeszkedés jóságát erősíti meg egy értéket felvevő RSQ (6.49. R-eredmény) és mü-érték (6.51. R-eredmény), valamint a nullához közeli fi-érték is (6.50. R-eredmény).
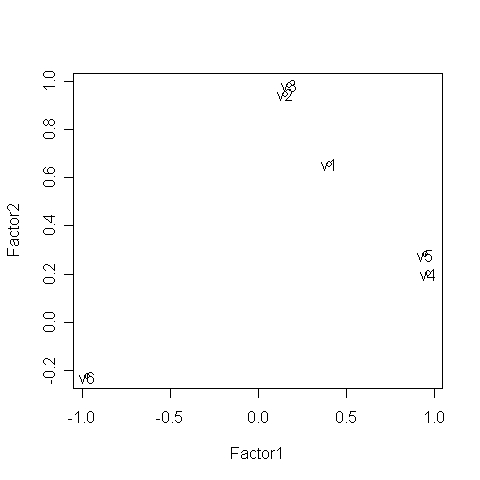
A 3.4.2 fejezetben már kiszámítottuk a példában szereplő adatokra a faktor-analízis faktorsúlyait. Mivel a többdimenziós skálázás is a korrelációkból indult ki, így összevethetjük a 6.46. R-eredményen szereplő és a 6.52. R-eredményen szereplő reprezentációkat. A 6.52. R-eredményen a faktorsúlyok pontdiagramját láthatjuk, melyet a 6.52. R-forráskód segítségével hívhatunk elő, felhasználva a 3.4. R-forráskódot is.
plot(FA$loadings)
text(FA$loadings,labels=rownames(d2))
|
| |
6.52. R-forráskód
|
Láthatjuk, hogy a két ábra szinte tükörképe egymásnak, vagyis mindkét módszerrel ugyanazt a geometriai reprezentációt kaptuk az adatokra.
Utolsó lépésként érdemes megnézni, hogy a klaszteranalízis is hasonló eredményt ad-e (6.53. R-forráskód).
klaszter<-hclust(dist)
plot(klaszter)
|
| |
6.53. R-forráskód
|
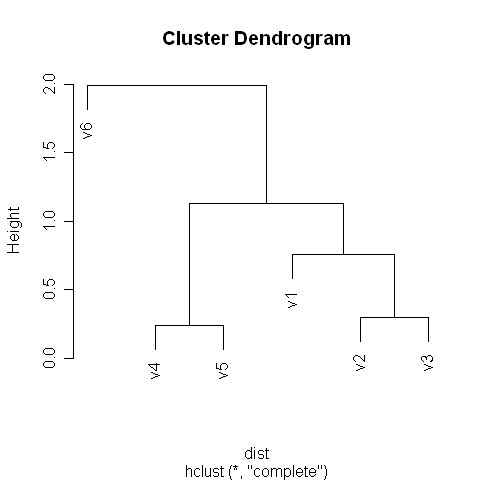
A 6.53. R-eredmény dendrogramja is ugyanazt sugallja, mint az előző két ábra: a 6-os item egy kissé távolabb van a többi változótól, a 4-es és az 5-ös szorosan összekapcsolódik, míg az 1-3 itemek is önálló klasztert, csoportot alkotnak.
|