|
6.5.3 probléma: Vállalatok vizsgálata
Harmadik példában sem távolságmátrixból indulunk ki. Visszatérünk az 5.6.4 példához, amelyben vállalatok egymáshoz való viszonyát vizsgáltuk a klaszteranalízis segítségével. Futtassuk le az 5.6.4 példánál található 5.27-5.29. R-forráskódot, melyek segítségével előhívjuk az adatokat és ismét megkapjuk a távolságmátrixot is (5.29. R-eredmény).
Ez tehát olyan példája a többdimenziós skálázásnak, amikor nyersadatokból indulunk ki, és az egyes esetek közötti távolságokat tartalmazza a távolságmátrix.
library(MASS)
mds<-isoMDS(távolságmátrix)
|
| |
6.35. R-forráskód
|
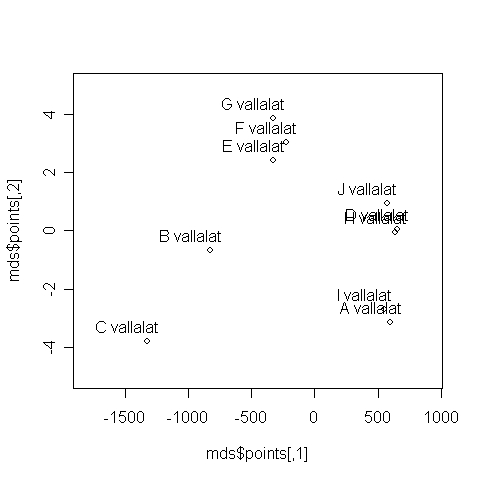
A 6.35. R-forráskód mutatja, hogyan futtathatjuk a többdimenziós skálázást. A 6.36. R-forráskód segítségével pedig megjeleníthetjük a kétdimenziós reprezentációt.
plot(mds$points,xlim=c(-1800,900),ylim=c(-5,5))
text(mds$points,labels=rownames(d),pos=3)
|
| |
6.36. R-forráskód
|
|
print(mds$points,digits=3)
|
| |
6.37. R-forráskód
|
[,1] [,2]
A vallalat 600 -3.1262
B vallalat -825 -0.6714
C vallalat -1325 -3.7827
D vallalat 654 0.0377
E vallalat -325 2.4353
F vallalat -225 3.0520
G vallalat -325 3.8541
H vallalat 640 -0.0540
I vallalat 555 -2.7010
J vallalat 575 0.9563
|
| |
6.37. R-eredmény.
|
A 6.37. R-eredmény segítségével pedig pontosan megtudhatjuk, hogy az egyes vállalatok milyen értékekkel szerepelnek az egyes dimenziókban. Most folytonos változók mérőszámai alapján készítettünk kétdimenziós ábrázolást, három változó adatai alapján kaptunk egy kétdimenziós geometriai reprezentációt, amely azt mutatja, hogy az emberek véleménye szerint az egyes vállalatok hogyan helyezkednek el egymáshoz képest.
Vizsgáljuk meg az illeszkedési mutatókat.
|
print(mds$stress,digits=3)
|
| |
6.38. R-forráskód
|
Első lépésben a Stess-értéket nézhetjük meg a 6.38. R-eredményen. Az értéke megfelelően kicsi, így elfogadhatjuk a kétdimenziós megoldást.
delta<-dist(mds$points)
plot(delta,távolságmátrix)
|
| |
6.39. R-forráskód
|
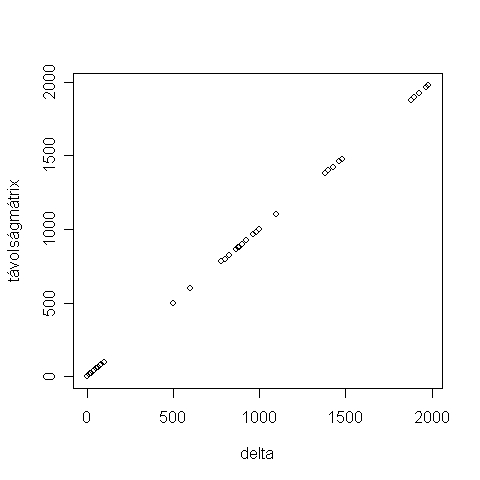
A Shepard-diagramon (6.39. R-eredmény) egy egyenesre illeszkednek az adatok, ami szintén a kétdimenziós megoldás jóságát erősíti meg. A 6.39. R-eredményen látható diagram y-tengelyén látható „távolságmátrix” az 5.29. R-forráskóddal előállított távolságmátrix elemeire utal.
Sh<-Shepard(dist,mds$points)
lm<-summary(lm(Sh$yf~Sh$x))
print(lm$r.squared,digits=3)
|
| |
6.40. R-forráskód
|
fi<-mds$stress^2/2
print(fi,digits=3)
|
| |
6.41. R-forráskód
|
mu<-cor(távolságmátrix,delta)
print(mu,digits=4)
|
| |
6.42. R-forráskód
|
Az illeszkedés jóságát erősíti meg egy értéket felvevő RSQ (6.40. R-eredmény) és mü-érték (6.42. R-eredmény), valamint a nullához közeli f-érték is (6.41. R-eredmény).
|