|
6.5.2 probléma: Autómárkák hasonlóságának vizsgálata
A második példában autómárkák közötti hasonlóságokat ítéltetünk meg a személyekkel. A 6.23. R-forráskóddal előhívható és a 6.23. R-eredményen látható adatbázisban az 1 érték jelenti a márkák teljes hasonlóságát, míg a 0 a hasonlóság hiányát.
|
d<-read.csv("c:/adat/autok.csv")
|
| |
6.23. R-forráskód
|
TOYOTACE AUDIA3 SEATIBIZ SKODAOCT MAZDAMX6 NISSANM SEATLEON FORDMOND
1 1.00 0.40 0.25 0.12 0.67 0.39 0.26 0.19
2 0.40 1.00 0.31 0.39 0.50 0.24 0.18 0.52
3 0.25 0.31 1.00 0.46 0.28 0.38 0.42 0.49
4 0.12 0.39 0.46 1.00 0.20 0.14 0.29 0.55
5 0.67 0.50 0.28 0.20 1.00 0.38 0.26 0.26
6 0.39 0.24 0.38 0.14 0.38 1.00 0.40 0.22
7 0.26 0.18 0.42 0.29 0.26 0.40 1.00 0.25
8 0.19 0.52 0.49 0.55 0.26 0.22 0.25 1.00
nevek
1 toyota celica
2 audi a3
3 seat ibiza
4 skoda octavia
5 mazda mx6
6 nissan micra
7 seat leon
8 ford mondeo
|
| |
6.23. R-eredmény.
|
A 6.23. R-eredményen most egy hasonlósági mátrixot láthatunk. A többdimenziós skálázás előtt a hasonlósági mátrixot távolságmátrixszá kell transzformálni. Ezt a 6.24. R-forráskód segítségével tehetjük meg. A transzformálás elméleti hátteréről a 6.4 fejezetben volt szó.
d2<-matrix(0,nrow=8,ncol=8)
for(i in 1:8) for (j in 1:8)d2[i,j]<-sqrt(d[i,i]-2*d[i,j]+d[j,j])
rownames(d2)<-d$nevek
print(d2,digits=3)
|
| |
6.24. R-forráskód
|
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
toyota celica 0.000 1.10 1.22 1.327 0.812 1.10 1.22 1.273
audi a3 1.095 0.00 1.17 1.105 1.000 1.23 1.28 0.980
seat ibiza 1.225 1.17 0.00 1.039 1.200 1.11 1.08 1.010
skoda octavia 1.327 1.10 1.04 0.000 1.265 1.31 1.19 0.949
mazda mx6 0.812 1.00 1.20 1.265 0.000 1.11 1.22 1.217
nissan micra 1.105 1.23 1.11 1.311 1.114 0.00 1.10 1.249
seat leon 1.217 1.28 1.08 1.192 1.217 1.10 0.00 1.225
ford mondeo 1.273 0.98 1.01 0.949 1.217 1.25 1.22 0.000
|
| |
6.24. R-eredmény.
|
A 6.24. R-eredmény az így kapott távolságértékeket tartalmazó mátrix szemlélteti. Ezután a 6.25. R-forráskód segítségével állítsuk be távolságmátrixként a 6.24. R-eredmény mátrixát. A 6.25. R-eredmény az immár tényleges távolságmátrixot szemlélteti.
dist<-as.dist(d2)
print(dist,digits=3)
|
| |
6.25. R-forráskód
|
toyota celica audi a3 seat ibiza skoda octavia mazda mx6
audi a3 1.095
seat ibiza 1.225 1.175
skoda octavia 1.327 1.105 1.039
mazda mx6 0.812 1.000 1.200 1.265
nissan micra 1.105 1.233 1.114 1.311 1.114
seat leon 1.217 1.281 1.077 1.192 1.217
ford mondeo 1.273 0.980 1.010 0.949 1.217
nissan micra seat leon
audi a3
seat ibiza
skoda octavia
mazda mx6
nissan micra
seat leon 1.095
ford mondeo 1.249 1.225
|
| |
6.25. R-eredmény.
|
library(MASS)
mds<-isoMDS(dist,k=3)
|
| |
6.26. R-forráskód
|
A távolságmátrix birtokában immár lefuttathatjuk a többdimenziós skálázást. Ez alkalommal háromdimenziós megoldást érdemes kérni, mivel a kétdimenziós megoldás Stress-értéke túl nagy.
x<-mds$points[,1]
y<-mds$points[,2]
z<-mds$points[,3]
|
| |
6.27. R-forráskód
|
library(Rcmdr)
scatter3d(x,y,z,surface.col=c("white"),point.col="blue")
identify3d(x,y,z,label=rownames(d2))
|
| |
6.28. R-forráskód
|
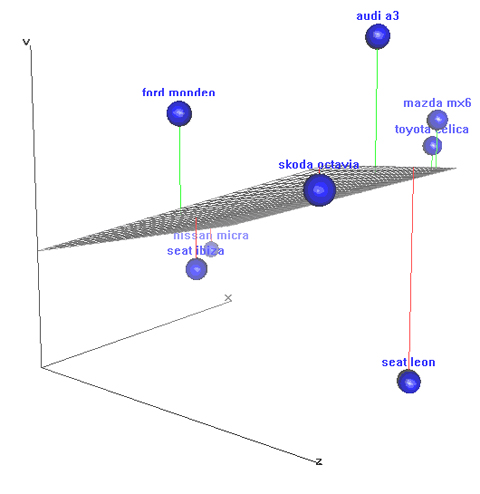
A többdimenziós skálázás lefuttatása után elsőként most is a háromdimenziós geometriai reprezentációt vesszük szemügyre. Ehhez elsőként az egyes dimenzióbeli értékeket rendeljük hozzá egy-egy változóhoz a 6.27. R-forráskód segítségével. A háromdimenziós ábrához elsőként az Rcmdr nevű bővítményt kell futtatni (6.28. R-forráskód). A 6.28. R-forráskód második sora az ábrakérés parancsa. Az x,y,z a 6.27. R-forráskód segítségével kialakított változókat takarja. Paraméterként megadhatjuk még a sík és az ábrázolt pontok színét is. Az utolsó sorral felcímkézhetjük az egyes pontokat. Fontos, hogy a parancssor futtatása után a felugró grafikus ablakon megjelenő ábrán az egér jobb gombjával kijelölve kapjuk meg az adott pont címkéjét. A geometriai reprezentáció értelmezését megkönnyítheti a 6.29. R-forráskóddal megjelenített egyes dimenzióbeli értékek (6.29. R-eredmény).
|
print(mds$points,digits=3)
|
| |
6.29. R-forráskód
|
[,1] [,2] [,3]
toyota celica 1.1344 -0.316 0.216
audi a3 -0.1037 -0.945 0.216
seat ibiza -0.5664 0.511 -0.319
skoda octavia -1.2233 -0.082 0.294
mazda mx6 0.8627 -0.497 0.269
nissan micra 0.7813 0.626 -0.751
seat leon 0.0629 1.184 0.308
ford mondeo -0.9479 -0.480 -0.232
|
| |
6.29. R-eredmény.
|
A 6.28. és a 6.29. R-eredmény együttes vizsgálata alapján elnevezhetjük az egyes dimenziókat. A kapott konfigurációban az első dimenziót, vagyis az x-tengelyt nevezhetjük az ár tengelyének. A második tengely, az y, a családbarát jellegre vonatozik, míg az utolsó, z dimenzió a sportosságot képviselheti.
|
print(mds$stress,digits=3)
|
| |
6.30. R-forráskód
|
Ezek után vizsgáljuk meg a jósági mutatókat. Első lépésben a Stess-értéket nézhetjük meg a 6.30. R-eredményen. Az értéke megfelelően kicsi, így elfogadhatjuk a háromdimenziós megoldást.
delta<-dist(mds$points)
plot(delta,dist)
|
| |
6.31. R-forráskód
|
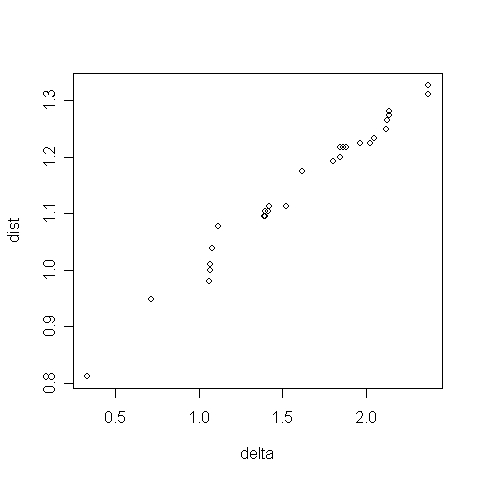
A Shepard-diagramon (6.31. R-eredmény) egy egyenesre illeszkednek az adatok, ami szintén a háromdimenziós megoldás jóságát erősíti meg.
Sh<-Shepard(dist,mds$points)
lm<-summary(lm(Sh$yf~Sh$x))
print(lm$r.squared,digits=4)
|
| |
6.32. R-forráskód
|
fi<-mds$stress^2/2
print(fi,digits=3)
|
| |
6.33. R-forráskód
|
mu<-cor(dist,delta)
print(mu,digits=4)
|
| |
6.34. R-forráskód
|
Az illeszkedés jóságát erősíti meg egyhez közeli RSQ (6.32. R-eredmény) és mü-érték (6.34. R-eredmény), valamint a nullához közeli f-érték is (6.33. R-eredmény).
|