|
6.5 Példák
6.5.1 probléma: Üdítőitalok vizsgálata
Az első példában különböző üdítőitalokat vizsgálunk meg a többdimenziós skálázás segítségével. A 6.13. R-forráskóddal előhívható adatbázisban különböző üdítőitalok távolságmátrixa szerepel.
d<-read.csv("c:/adat/kola.csv")
print(d)
|
| |
6.13. R-forráskód
|
szörp hohesC savm.asv.viz szobi traubi fantanarancs asv.viz
1 0.00 0.48 0.66 0.19 0.72 0.94 0.89
2 0.48 0.00 0.45 0.30 0.32 0.40 0.56
3 0.66 0.45 0.00 0.44 0.38 0.56 0.38
4 0.19 0.30 0.44 0.00 0.48 0.68 0.67
5 0.72 0.32 0.38 0.48 0.00 0.20 0.30
6 0.94 0.40 0.56 0.68 0.20 0.00 0.45
7 0.89 0.56 0.38 0.67 0.30 0.45 0.00
NEVEK
1 szörp
2 hohesC
3 savm.ásv.víz
4 szobi
5 traubi
6 fantanarancs
7 asv.viz
|
| |
6.13. R-eredmény.
|
Az embereknek azt kellett megítélni, hogy az egyes üdítők mennyire különböznek egymástól. A 0 érték azt jelenti, hogy teljesen egyformák az italok, míg az 1 a lehető legnagyobb mértékű különbözőséget jelzi.
m<-as.matrix(d[1:7])
rownames(m)<-d$NEVEK
dist<-as.dist(m)
dist
|
| |
6.14. R-forráskód
|
Mivel a többdimenziós skálázás távolságmátrixból indul ki, ezért a 6.13. R-eredményen szereplő távolságmátrixot állítsuk be úgy, hogy az R is távolságmátrixként kezelje. Ezt a 6.14. R-forráskód segítségével tehetjük meg. Az így kapott távolságmátrixot a 6.14. R-eredmény mutatja.
szörp hohesC savm.ásv.víz szobi
hohesC 0.48
savm.ásv.víz 0.66 0.45
szobi 0.19 0.30 0.44
traubi 0.72 0.32 0.38 0.48
fantanarancs 0.94 0.40 0.56 0.68
asv.viz 0.89 0.56 0.38 0.67
traubi fantanarancs
hohesC
savm.ásv.víz
szobi
traubi
fantanarancs 0.20
asv.viz 0.30 0.45
|
| |
6.14. R-eredmény.
|
library(MASS)
mds<-isoMDS(dist,k=2)
|
| |
6.15. R-forráskód
|
A távolságmátrix kialakítása után már futtathatjuk a többdimenziós skálázást a 6.15. R-forráskódnak megfelelően.
plot(mds$points,xlim=c(-1,1),ylim=c(-0.5,0.5))
text(mds$points,labels=rownames(m),pos=1)
|
| |
6.16. R-forráskód
|
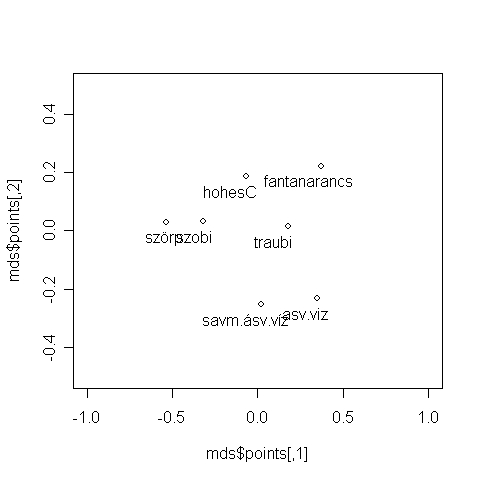
A 6.16. R-forráskóddal kérhetjük a kétdimenziós ábrát a többdimenziós skálázás eredményéről. A 6.16. R-eredményen láthatjuk, hogy az adatok hogyan helyezkednek el egymáshoz viszonyítva a kétdimenziós térben. Mielőtt alaposabban elemeznénk az ábrát, vizsgáljuk meg a jósági mutatókat.
|
print(mds$stress,digits=3)
|
| |
6.17. R-forráskód
|
Első lépésben a Stess-értéket nézhetjük meg a 6.17. R-eredményen. Az értéke megfelelően kicsi, így elfogadhatjuk a kétdimenziós megoldást.
delta<-dist(mds$points)
plot(delta,dist)
|
| |
6.18. R-forráskód
|
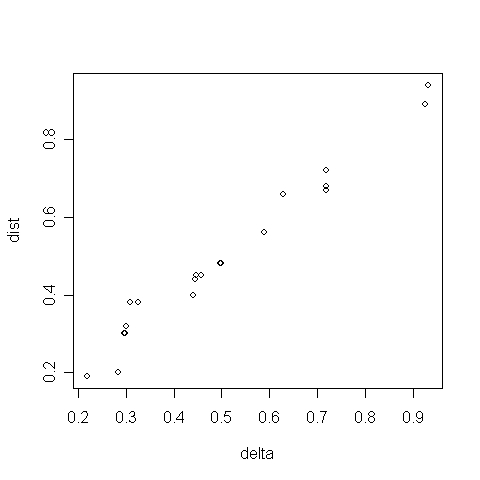
A Shepard-diagramon (6.18. R-eredmény) egy egyenesre illeszkednek az adatok, ami szintén a kétdimenziós megoldás jóságát erősíti meg.
Sh<-Shepard(dist,mds$points)
lm<-summary(lm(Sh$yf~Sh$x))
print(lm$r.squared,digits=3)
|
| |
6.19. R-forráskód
|
fi<-mds$stress^2/2
print(fi,digits=3)
|
| |
6.20. R-forráskód
|
mu<-cor(dist,delta)
print(mu,digits=3)
|
| |
6.21. R-forráskód
|
Az illeszkedés jóságát erősíti meg egyhez közeli RSQ (6.19. R-eredmény) és mü-érték (6.21. R-eredmény), valamint a nullához közeli f-érték is (6.20. R-eredmény).
Az illeszkedés jóságát vizsgáló mutatók ismeretében már interpretálhatjuk a 6.16. R-eredményen látható geometriai reprezentációt. Ehhez segítségképpen a 6.22. R-forráskóddal kérjük le az egyes objektumok koordinátáit is.
|
print(mds$points,digits=3)
|
| |
6.22. R-forráskód
|
[,1] [,2]
szörp -0.5387 0.0304
hohesC -0.0657 0.1862
savm.ásv.víz 0.0235 -0.2521
szobi -0.3195 0.0317
traubi 0.1798 0.0138
fantanarancs 0.3726 0.2233
asv.viz 0.3480 -0.2332
|
| |
6.22. R-eredmény.
|
A Magyarország városait bemutató példában egyértelmű volt az egyes koordinátatengelyek, dimenziók elnevezése. Ám egy ilyen példánál már nagyobb gondot okozhat. A 6.16. és a 6.22. R-eredmény alapján láthatjuk, hogy az első dimenzióban az ásványvíz és a Fanta Narancs szerepel magas értékekkel, viszonylag kis értéke van a Szobi gyümölcslének és a szörpnek. A második dimenzióiban is magas értékkel szerepel a Fanta és a Hohes C, viszont extrém alacsonnyal az ásványvíz. Ezek alapján az első dimenzió képviselheti a szénsavtartalmat, míg a második a gyümölcstartalmat. A feladatban szereplő emberek fejében ez a két szempont tűnt fontosnak az üdítőitalok különbözőségének megítélése során.
|