|
5.3.1.2 Teljes lánc, avagy a legtávolabbi szomszéd elve
Ezen elv alapján két klaszter közötti távolság a két legtávolabbi pontjuk távolsága. Példaként most is nézzük az 5.1. táblázat adatait. Első lépésként most is a hármas és a négyes elemet vonjuk össze, hiszen ez a két elem van egymáshoz a legközelebb (két egységnyi). Ekkor a távolságok a legtávolabbi szomszéd elve alapján az 5.5. táblázatnak megfelelően alakulnak.
| |
| |
1 |
2 |
(3,4) |
5 |
| 1 |
0 |
|
|
|
| 2 |
3 |
0 |
|
|
| (3,4) |
10 |
9 |
0 |
|
| 5 |
9 |
8 |
5 |
0 |
|
|
| |
5.5. táblázat. |
|
Az 5.5. táblázaton láthatjuk, hogy a következő legkisebb távolság a 3 egység, ez alapján a következő lépésben az első két elemet vonjuk össze. A távolságok most az 5.6. táblázatnak megfelelően alakulnak.
| |
| |
(1,2) |
(3,4) |
5 |
| (1,2) |
0 |
|
|
| (3,4) |
10 |
0 |
|
| 5 |
9 |
5 |
0 |
|
|
| |
5.6. táblázat. |
|
Az 5.6. táblázat alapján a legkisebb távolság most az 5 egység. Ezért most az ötös elemet bevonjuk a hármas és a négyes elem által alkotott klaszterbe. Ezáltal most már csak két klaszter maradt, ahogyan azt az 5.7. táblázatban is láthatjuk.
| |
| |
(1,2) |
(3,4,5) |
| (1,2) |
0 |
|
| (3,4,5) |
10 |
0 |
|
|
| |
5.7. táblázat. |
|
A maradék két klasztert tíz egységnyi távolságnál vonhatjuk össze, így az összes elem egyetlen klaszterbe kerül. A lépéseket az 5.8. táblázat foglalja össze.
| |
| 0 |
1,2,3,4,5 |
| 2 |
1,2,(3,4),5 |
| 3 |
(1,2),(3,4),5 |
| 5 |
(1,2),(3,4,5) |
| 10 |
(1,2,3,4,5) |
|
|
| |
5.8. táblázat. |
|
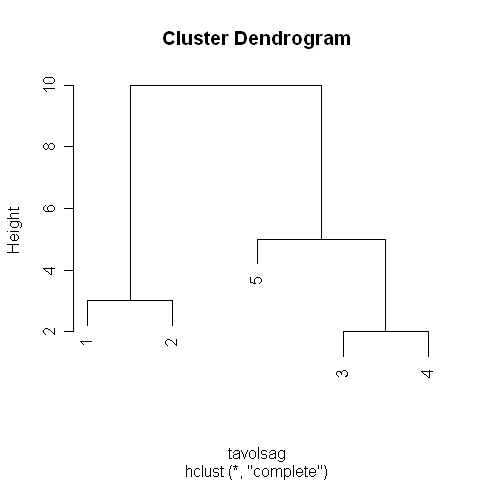
klaszter<-hclust(tavolsag,method="complete")
plot(klaszter)
|
| |
5.7. R-forráskód
|
Az 5.7. R-forráskóddal az R-ben is lefuttathatjuk a klaszteranalízist, a kapott dendrogramot az 5.7. R-eredmény mutatja. Az 5.8 és az 5.9. R-eredményen pedig ismét az 5.8. táblázat adatait láthatjuk, ahogyan azt már az egyszerű lánc módszernél is láthattuk.
[,1] [,2]
[1,] -3 -4
[2,] -1 -2
[3,] -5 1
[4,] 2 3
|
| |
5.8. R-eredmény.
|
|