|
5.3.1.1 Egyszerű lánc, avagy a legközelebbi szomszéd elve
Ez a módszer a legkisebb távolságon, a legközelebbi szomszéd elvén alapul. Először az a két megfigyelési egység kerül egy klaszterbe, amelyek között a legkisebb a távolság. Ezután a következő legkisebb távolság kerül meghatározásra. Minden lépésnél a két klaszter közötti távolság a két legközelebbi pontjuk közötti távolság. Két klaszter akkor vonunk össze, ha a közöttük lévő távolság a legrövidebb.
Példaként nézzük az 5.1. táblázat adatait. Először az a két elem kerül egy klaszterbe, amelyek között a legkisebb a távolság. A táblázatban szereplő legkisebb távolság a harmadik és a negyedik elem közötti négy egység. Vagyis először a harmadik és a negyedik elem kerül egy klaszterbe. A többi elem önálló klasztert alkot, így összesen 4 klaszterünk van. A távolságok a legkisebb szomszéd elve alapján az 5.2. táblázatnak megfelelően alakulnak.
A következő legkisebb távolság a három egység (5.2. táblázat). Ennyi a távolság az első és a második elem között, valamint a legközelebbi szomszéd elve alapján az ötödik elem valamint a harmadik és a negyedik elem által alkotott klaszter között. Ezáltal most 2 klaszterünk van (5.3. táblázat). A következő legkisebb távolság az öt egység. Ennyi a távolság a legkisebb szomszéd elve alapján a két klaszter között, így ezzel a lépéssel az összes elemet bevontuk a klaszterbe. Ezeket a lépéseket az 5.4. táblázat foglalja össze.
| |
| |
1 |
2 |
3 |
4 |
5 |
| 1 |
0 |
3 |
5 |
10 |
9 |
| 2 |
3 |
0 |
6 |
9 |
8 |
| 3 |
5 |
6 |
0 |
2 |
3 |
| 4 |
10 |
9 |
2 |
0 |
5 |
| 5 |
9 |
8 |
3 |
5 |
0 |
|
|
| |
5.1. táblázat. |
|
| |
| |
1 |
2 |
(3,4) |
5 |
| 1 |
0 |
|
|
|
| 2 |
3 |
0 |
|
|
| (3,4) |
5 |
6 |
0 |
|
| 5 |
9 |
8 |
3 |
0 |
|
|
| |
5.2. táblázat. |
|
| |
| |
(1,2) |
(3,4,5) |
| (1,2) |
0 |
|
| (3,4,5) |
5 |
0 |
|
|
| |
5.3. táblázat. |
|
| |
| 0 |
1,2,3,4,5 |
| 2 |
1,2,(3,4),5 |
| 3 |
(1,2),(3,4,5) |
| 5 |
(1,2,3,4,5) |
|
|
| |
5.4. táblázat. |
|
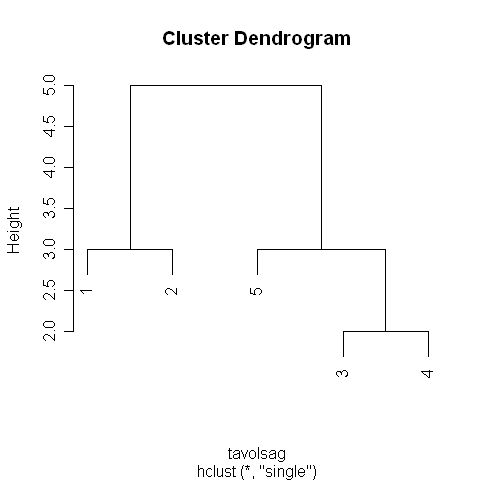
A hierarchikus klaszter-módszereknél a klasztereket úgynevezett dendrogramokkal ábrázolják. A dendrogramokat elkészíthetjük az R-program segítségével.
Első lépésként az 5.1. táblázatban látható távolságmátrixot kell bevinnünk. Ehhez az 5.1. R-forráskódnak megfelelően soronként kell bevinni a szimmetrikus távolságmátrix adatait.
|
m=c(0,3,5,10,9,3,0,6,9,8,5,6,0,2,3,10,9,2,0,5,9,8,3,5,0)
|
| |
5.1. R-forráskód
|
matrix<-matrix(m,nrow = 5, ncol = 5)
print(matrix)
|
| |
5.2. R-forráskód
|
Ezt követően az 5.2. R-forráskód segítségével mátrixszá alakíthatjuk adatainkat. A „nrow” paraméterrel adhatjuk meg a mátrix sorainak, míg a „ncol” paranccsal a mátrix oszlopainak a számát. Magát a mátrixot az 5.2. R-eredményen láthatjuk.
[,1] [,2] [,3] [,4] [,5]
[1,] 0 3 5 10 9
[2,] 3 0 6 9 8
[3,] 5 6 0 2 3
[4,] 10 9 2 0 5
[5,] 9 8 3 5 0
|
| |
5.2. R-eredmény.
|
Ezután meg kell mondani az R-nek, hogy kezelje távolságmátrixként a mátrixot (5.3. R-forráskód és R-eredmény).
tavolsag<-as.dist(matrix)
print(tavolsag)
|
| |
5.3. R-forráskód
|
1 2 3 4
2 3
3 5 6
4 10 9 2
5 9 8 3 5
|
| |
5.3. R-eredmény.
|
Ha ezzel készen vagyunk, akkor kérhetünk egy klaszterelemzést (5.4. R-forráskód). Ezt a „hclust” paranccsal tehetjük meg. Az egyszerű lánc módszert a „method” paraméterrel lehet beállítani.
klaszter<-hclust(tavolsag,method="single")
plot(klaszter)
|
| |
5.4. R-forráskód
|
A kapott dendrogramot az 5.4. R-eredmény mutatja.
Az 5.4. táblázatot természetesen az R segítségével is megkaphatjuk. Az 5.5. R-forráskóddal kapott 5.5. R-eredmény az összevonás menetét mutatja, az 5.6. R-eredmény pedig azt, hogy milyen távolságnál történtek az összevonások.
[,1] [,2]
[1,] -3 -4
[2,] -1 -2
[3,] -5 1
[4,] 2 3
|
| |
5.5. R-eredmény.
|
Az 5.5. és az 5.6. R-eredményt párhuzamosan érdemes vizsgálni. Az 5.6. R-eredmény mutatja, hogy az első összevonás 2 egységnyi távolságnál történt, ekkor a hármas és a négyes elemet vontuk össze, ez már az 5.5. R-eredményen láthatjuk. És így tovább, ahogyan az 5.4. táblázatban is láthattuk. Az 5.5. R-eredményen látható, az összevonás folyamatát személtető mátrix elemei lehetnek pozitívak vagy negatívak. Ha az elem negatív, akkor az egyes elemek összevonását mutatja, míg a pozitív elemek a szám által jelzett lépésben összevont, korábban kialakított klaszterre utal. Például a harmadik sorban a az 5-ös elemet az első lépésben (3 és 4-es elemből) kialakított klaszterrel vonjuk össze.
|