5.6.2 probléma: Vásárlói attitűdök vizsgálata

Vásárolni mindenki szokott. Van, akinek szenvedélye a vásárlás, mások, pedig ha csak lehet, kerülik az üzleteket. Ebben a példában annak fogunk utánajárni, hogy milyen tipikus vásárlási attitűdök vannak. A vizsgálathoz szükséges adatokat az 5.21. R-forráskóddal hívhatjuk elő.

Az 5.21. R-eredményen látható változók kódja a következő:

• V1: Általában igyekszem diszkont áruházakban vásárolni.
• V2: Imádok vásárolgatni.
• V3: Mindig figyelem az árleszállításokat.
• V4: A vásárlás számomra szinte egy hobbi.
• V5: Ha csak tehetem, nem én vásárolok.
• V6: Szívesen járom az üzleteket baráti társaságban.

   V1 V2 V3 V4 V5 V6
1   6  4  7  3  2  4
2   2  3  1  4  5  4
3   7  2  6  4  1  3
4   4  6  4  5  3  6
5   1  3  2  2  6  4
6   6  4  6  2  3  4
7   5  3  6  3  3  4
8   7  3  7  4  1  4
9   2  4  3  3  6  3
10  3  5  3  6  4  6
11  1  3  2  3  5  3
12  8  4  5  4  2  4
13  2  2  1  5  4  4
14  4  6  4  6  4  7
15  6  5  4  2  2  4
16  3  5  4  8  4  7
17  4  4  7  2  2  5
18  3  7  2  6  4  3
19  4  6  3  7  2  7
20  3  3  2  4  7  2

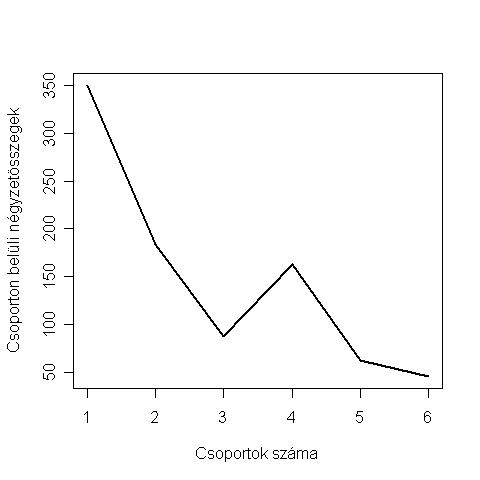
Első lépésként a csoporton belüli négyzetösszegeket ábrázoljuk a lehetséges klaszterszámok függvényében, hogy el tudjuk dönteni, hány klaszteres megoldás lenne a megfelelő az adatokra (5.22. R-forráskód).

5.22. R-eredmény.

Az 5.22. R-eredményen azt láthatjuk, hogy a hármas értéknél van törés a görbén, ez alapján  a háromklaszteres megoldást fogjuk vizsgálni k-középpontú klaszteranalízissel (5.23. R-forráskód).

  K-means clustering with 3 clusters of sizes 8, 6, 6 

Cluster means:
    V1   V2   V3   V4  V5   V6
1 6.13 3.63 6.00 3.00 2.0 4.00
2 1.83 3.00 1.83 3.50 5.5 3.33
3 3.50 5.83 3.33 6.33 3.5 6.00 

Clustering vector:
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 
 1  2  1  3  2  1  1  1  2  3  2  1  2  3  1  3  1  3  3  2  

Within cluster sum of squares by cluster:
[1] 36.8 22.0 28.5 

Available components:
[1] "cluster"  "centers"  "withinss" "size"    

Az 5.23. R-eredmény a klaszteranalízis eredményét mutatja. Az első sor („K-means clustering with 3 clusters of sizes 8,6,6”) arról ad információt, hogy háromklaszteres megoldásunk van, melyek mérete 8, illetve 6, 6 elemszám. Hogy az egyes elemek melyik klaszterbe esnek, arról a „Clustering vector” ad információt. Az első sor az egyes elemeket, a második pedig a csoporttagságot mutatja.

A „Cluster means” az egyes klaszterek átlagos tagjának, centroidjának a jellemzőit mutatják. Az első klaszter átlagos tagja igyekszik diszkontáruházakban és árleszállításokon vásárolni, minél több pénzt megtakarítani. A második klaszter átlagos tagja ha csak teheti, másokkal vásároltat be. Míg a harmadik klaszter átlagos tagja szenvedélyes vásárló, baráti társaságokkal is szívesen járja az üzleteket.

A „Within cluster sum of squares by cluster” értékei a klaszteren belüli eltérések négyzetösszegét mutatja.

Az eredmények alapján vannak olyan emberek, akik nem szeretnek vásárolni, s vannak olyanok, akiknek egyfajta hobbi a vásárlás. Ugyanakkor vannak megfontoltabb emberek is, akik igyekeznek takarékossági szempontokat is figyelembe venni, és minél olcsóbban elintézni a bevásárlásokat.