|
5.6 Példák
5.6.1 probléma: Csokoládémárkák vizsgálata
A klaszteranalízissel elemzett első problémában csokoládémárkákat vizsgálunk. Összesen tíz csokimárkát ítéltek meg a személyek a csoki nagysága, krémességének és töménységének tekintetében. Azt fogjuk megvizsgálni, hogy mely csokoládék állnak a vizsgálati személyek szerint közel egymáshoz. Ennek ismerete hasznos lehet marketing szempontból - például mely csokoládékat érdemes közel tenni egymáshoz a polcon.
Az adatokat tartalmazó file-t az 5.15. R-forráskód segítségével nyithatjuk meg.
|
d<-read.csv("c:/adat/csoki.csv")
|
| |
5.15. R-forráskód
|
CSOKI NAGYSÁG KRÉMES TÖMÉNY
1 Boci 10 9 7
2 Milka 10 10 8
3 Tibi 9 8 6
4 Balaton 4 5 6
5 Müzliszel 4 2 4
6 3-bit 3 7 7
7 Kapuciner 2 5 7
8 Mars 5 7 8
9 Snickers 5 7 9
10 Sportszel 4 8 9
|
| |
5.15. R-eredmény.
|
Az 5.15. R-eredményen láthatjuk, hogy most nem távolságmátrixszal dolgozunk, hanem „eredeti” változókkal. Az adatokból számított távolságmátrixot természetesen elkészíthetjük az R segítségével is. Ehhez első lépésként azt kell tudatnunk a programmal, hogy az első változó, a „CSOKI”, az egyes elemek neveit tartalmazza. Ez azért hasznos, mert így a kapott dendrogram levelein a csokoládék neveit fogjuk látni, nem pedig számokat. Ezáltal sokkal áttekinthetőbb ábrát fogunk kapni és könnyebben tudjuk azonosítani az egyes klasztereket. Ezt az 5.16. R-forráskóddal tudjuk megtenni.
Ezután kiszámíttathatjuk a távolságmátrixot az adatokra. A távolságmátrix kiszámítása az 5.17. R-forráskódon látható. Láthatjuk, hogy az első változót kihagyjuk a mátrixból, hiszen az csak a csokoládéneveket tartalmazza, egyéb adatot nem. A tényleges távolságmátrixot az 5.17. R-eredményen láthatjuk.
távolságmátrix<-dist(d[2:4])
print(távolságmátrix, digits=3)
|
| |
5.17. R-forráskód
|
Boci Milka Tibi Balaton
Milka 1.41
Tibi 1.73 3.00
Balaton 7.28 8.06 5.83
Müzliszel 9.70 10.77 8.06 3.61
3-bit 7.28 7.68 6.16 2.45
Kapuciner 8.94 9.49 7.68 2.24
Mars 5.48 5.83 4.58 3.00
Snickers 5.74 5.92 5.10 3.74
Sportszel 6.40 6.40 5.83 4.24
Müzliszel 3-bit Kapuciner Mars
Milka
Tibi
Balaton
Müzliszel
3-bit 5.92
Kapuciner 4.69 2.24
Mars 6.48 2.24 3.74
Snickers 7.14 2.83 4.12 1.00
Sportszel 7.81 2.45 4.12 1.73
Snickers
Milka
Tibi
Balaton
Müzliszel
3-bit
Kapuciner
Mars
Snickers
Sportszel 1.41
|
| |
5.17. R-eredmény.
|
A távolságmátrix birtokában már futtathatunk egy klaszteranalízist, az egyszerű lánc módszert használva a klaszterképzéshez (5.18. R-forráskód).
|
klaszter<-hclust(távolságmátrix, method="single")
|
| |
5.18. R-forráskód
|
[,1] [,2]
[1,] -8 -9
[2,] -1 -2
[3,] -10 1
[4,] -3 2
[5,] -4 -7
[6,] -6 5
[7,] 3 6
[8,] -5 7
[9,] 4 8
|
| |
5.19. R-eredmény.
|
magasság<-klaszter$height
print(magasság,digits=3)
|
| |
5.20. R-forráskód
|
[1] 1.00 1.41 1.41 1.73 2.24 2.24 2.24 3.61 4.58
|
| |
5.20. R-eredmény.
|
Az 5.19-5.20. R-eredményen láthatjuk, hogy a klaszterek kialakítása 9 lépésben történt és legutolsó elemet 4,58-as távolságnál vontuk be a klaszterbe.
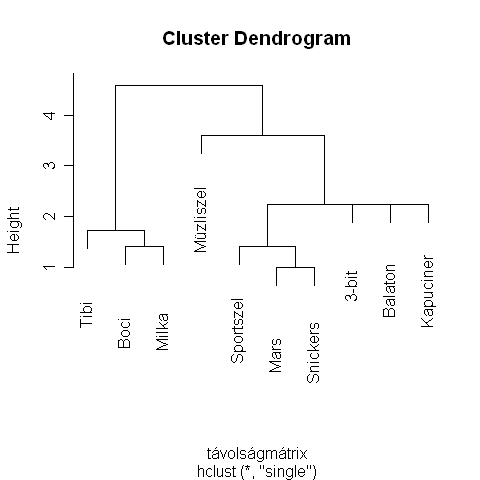
Az 5.18. R-eredményen pedig a dendrogram látható. Láthatjuk, hogy alapvetően két nagy csoportja van a vizsgált csokoládéknak. Az egyikbe tartoznak a táblás csokoládék (Tibi, Milka és a Boci), míg a másikba a szeletes csokik. Az utóbbiba vonta be a módszer a müzliszeletet is, bár meglehetősen távol van a többi csokoládétól.
|