|
4.6 Egy teljes körű példa: szalagmunkások vizsgálatának folytatása
A 4.2 fejezetben részletesen szó volt a szalagmunkások alkalmasság-vizsgálatáról. Ebben a fejezetben az előzőekben ismertetett diszkriminancia-analízis segítségével igyekszünk objektíven szemügyre venni a példát.
Első lépésként vigyük be a 4.1. táblázatban látható adatokat az R statisztikai program segítségével (4.1. R-forráskód).
d<-data.frame(bevalas=c(1,1,0,1,0,1,0,0,1,0), figyelem=c(1,1,2,2,3,3,4,4,4,6),
monoton=c(2,5,1,3,2,4,3,1,6,5))
|
| |
4.1. R-forráskód
|
library(lattice)
xyplot(monoton~figyelem, groups=bevalas, data=d, cex=2,pch=20)
|
| |
4.2. R-forráskód
|
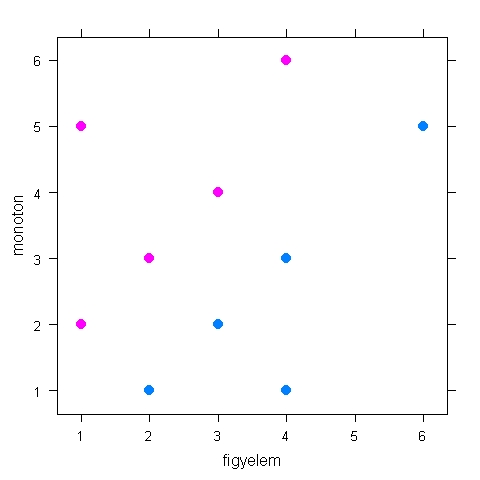
Ezt követően próbáljuk meg pontdiagrammal ábrázolni az adatokat. A 4.2. R-forráskód mutatja, hogyan lehet ezt megtenni. A 4.2. R-eredmény sajátossága, hogy a pontdiagramon az egyes csoportokhoz tartozó adatokat eltérő színek jelzik. A két csoport szemmel láthatóan szétválik egymástól, ám sem a függőleges, sem a vízszintes tengely mentén nem lehet elkülöníteni a csoportokat.
A 3. Interaktív illusztrációval érzékeltetjük két csoport szétválasztásának problémáját.
t.test1<-t.test(figyelem~bevalas, data=d)
print(t.test1, digits=3)
|
| |
4.3. R-forráskód
|
Welch Two Sample t-test
data: figyelem by bevalas
t = 1.8116, df = 7.871, p-value = 0.108
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.4424492 3.6424492
sample estimates:
mean in group 0 mean in group 1
3.8 2.2
|
| |
4.3. R-eredmény.
|
t.test2<-t.test(monoton~bevalas, data=d)
print(t.test2, digits=3)
|
| |
4.4. R-forráskód
|
Welch Two Sample t-test
data: monoton by bevalas
t = -1.5541, df = 7.974, p-value = 0.159
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.9755013 0.7755013
sample estimates:
mean in group 0 mean in group 1
2.4 4.0
|
| |
4.4. R-eredmény.
|
A diszkrimnancia-analízis sajátossága, hogy a csoportokat magyarázó változók együttes figyelembevételével tudja szétválasztani. Azaz t-próbával nem tudunk szignifikáns különbségeket kimutatni a csoportátlagok között. Éppen ezért a diszkriminancia elemzés előtt végezzük el a t-statisztikát a figyelem és a monotónia-tűrés változójára is (4.3-4.4. R-forráskód). Mind a 4.3., mind a 4.4. R-forráskód sziginikancia szintje azt mutatja, hogy a csoportátlagok között nincs különbség („p-value = 0.108”, illetve „p-value = 0.159”). Nézzük meg, hogy többváltozós variancia-analízissel szét tudjuk-e választani a csoportokat.
man<-manova(cbind(figyelem,monoton)~bevalas, data=d)
DA<-summary(man, test="Wilks")
print(DA, digits=3)
|
| |
4.5. R-forráskód
|
Df Wilks approx F num Df den Df Pr(>F)
bevalas 1 0.2708 9.4247 2 7 0.01033 *
Residuals 8
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
|
| |
4.5. R-eredmény.
|
Az elemzés első lépése, hogy MANOVA-val megnézzük, valóban létezik-e két csoportja a munkásoknak beválás tekintetében. A 4.4. R-forráskód első sorában először azt adjuk meg, hogy mely változók alapján (jelen esetben a figyelem és a monoton változók tekintetében) mely változó csoportjait (jelen példában a beválás változó csoportjait) szeretnénk szétválasztani. Vagyis a figyelem és a monotóniatűrés vizsgálata alapján szeretnénk előrejelezni, hogy valaki megfelel-e szalagmunkára vagy sem. Továbbá megadhatjuk azt is, hogy mely statisztikai próbát alkalmazzuk a csoportok szétválasztásának tesztelésére. Az egyik legelterjedtebb módszer a Wilks-féle lambda, melyről részletesen a 4.8.3 mellékletben van szó. A 4.5. R-eredményen látható MANOVA táblázat F-statisztikához tartozó szignifikancia-szintje (0.01) annyit árul el nekünk, hogy a bevált és a nem bevált munkások csoportja különbözik egymástól.
Mindezek után a 4.6. R-forráskóddal kérjünk egy tényleges diszkriminancia-analízist. Ehhez futtatnunk kell a MASS elnevezésű bővítményt (erre utal az első sorban lévő library(MASS) parancs).
library(MASS)
diszkr<-lda(bevalas~figyelem+monoton, data=d)
print(diszkr, digits=3)
|
| |
4.6. R-forráskód
|
Call:
lda(bevalas ~ figyelem + monoton, data = d)
Prior probabilities of groups:
0 1
0.5 0.5
Group means:
figyelem monoton
0 3.8 2.4
1 2.2 4.0
Coefficients of linear discriminants:
LD1
figyelem -0.998
monoton 0.837
|
| |
4.6. R-eredmény.
|
A 4.6. R-eredményen láthatjuk a diszkriminancia-analízis eredményeit. Az első sor csupán a modellt mutatja, amit a 4.6. R-forráskódban megadtunk. Ezután következnek a függő változó csoportjainak az előzetes valószínűségei. Vagyis meg tudjuk mondani, hogy ha eltekintünk a független változóktól, mekkora annak a valószínűsége, hogy valaki az egyik vagy a másik csoportba tartozik, azaz - jelen példánál maradva - mekkora a valószínűsége, hogy valaki beválik vagy sem. Alapbeállításként az R úgy veszi, hogy egyenlő eséllyel tartozhatnak az egyik, vagy a másik csoportba a személyek. Ezután a „group means” címszó alatt az egyes csoportok átlagait láthatjuk. Azok, akik nem váltak be, a figyelem teszten átlagosan 3,8, míg monotónia-tűrés vizsgálaton átlagosan 2,4 pontot kaptak. Ugyanakkor azok, akik beváltak, a figyelem teszten átlagosan 2,2, míg monotónia-tűrés vizsgálaton átlagosan 4 pontot kaptak. Vagyis azok, akik nem váltak be, a monotónia-tűrés tesztben gyengébb teljesítményt nyújtottak, a figyelem tesztben pedig egy jobbat, míg akik beváltak, a monotónia-tűrés tesztben igen jó teljesítményt értek el, a figyelem tesztben pedig valamivel gyengébbet. Legvégül pedig a kanonikus diszkriminancia együtthatókat láthatjuk, melyek alapján felírhatjuk a kanonikus diszkriminancia-függvényt a következő módon:
Z = -0,998 * figyelem + 0,837 * monoton
Az eddig vizsgált adatokban előzetesen tudtuk a személyről, hogy bevált-e vagy sem, vagyis ismertük a tényleges csoporttagságát. Ám a diszkriminancia-analalízisnek célja az is, hogy előre jelezzük a csoporttagságokat, vagyis a figyelem és monotónia-tűrés tekintetében megmondjuk egy személyről, hogy nagy valószínűséggel beválik-e vagy sem. Ezt tesszük most a 4.7. és a 4.8. R-forráskóddal. Az első személy a figyelem teszten 2, míg a monotónia-tűrés teszten 4 pontot kapott, míg a második személy pontszámai ebben a sorrendben 6 és 1.
newdata<-rbind(c(2,4),c(6,1))
dimnames(newdata)<-list(NULL,c("figyelem","monoton"))
newdata<-data.frame(newdata)
pred<-predict(diszkr,newdata=newdata)
|
| |
4.7. R-forráskód
|
|
print(pred$posterior,digits=3)
|
| |
4.8. R-forráskód
|
0 1
1 0.00743 9.93e-01
2 1.00000 6.86e-07
|
| |
4.8. R-eredmény.
|
A 4.8. R-eredmény alapján az első személy nagy valószínűséggel az 1-gyel kódolt, míg a második személy a 0-val kódolt csoportba tartozik. Vagyis az első személyt alkalmasnak, míg a másodikat alkalmatlannak ítélhetjük a szalagmunkára.
csoport<-predict(diszkr,method="plug-in")$class
table<-table(csoport,d$bevalas)
table
|
| |
4.9. R-forráskód
|
n<-length(csoport)
helyes<-table[1]+table[4]
helyes*100/n
|
| |
4.10. R-forráskód
|
Az utolsó mozzanat, amit még érdemes elvégeznünk a diszkriminancia-analízis esetében, az nem más, mint magának az analízisnek az értékelése. Ehhez általánosan használt módszer, ha összevetjük a tényleges és a becsült csoporttagságot, és megállapítjuk, az adatok mekkora részét tudjuk helyesen besorolni az alkotott modell alapján. Ezt a 4.9. R-forráskóddal tudjuk megtenni, az eredményt pedig a 4.9. R-eredményen láthatjuk. A táblázatban vízszintesen látható a becsült csoporttagság, függőlegesen pedig a valódi. Mivel az összes adat a főátlóban van, így megállapíthatjuk, hogy a modell alapján az összes adatot helyesen kategorizáltuk. A 4.10. R-forráskód mutatja, hogyan lehet a helyes besorolás arányát százalékosan kiszámítani. Mivel az összes, adatot helyesen kategorizáltuk, így ez az arány 100% (4.10. R-eredmény).
|