2.3.4 Főkomponensek számának meghatározása

Most nézzük meg a főkomponens-analízis segítségével, hogy valóban jól reprezentálhatóak-e az adatok egyetlen főkomponens, egyetlen mérőszám segítségével, vagyis futtassuk le a főkomponens-analízist az adatokra.

Importance of components:
                        PC1   PC2     PC3     PC4
Standard deviation     2.75 0.649 0.27196 0.26215
Proportion of Variance 0.93 0.052 0.00912 0.00847
Cumulative Proportion  0.93 0.982 0.99153 1.00000

A 2.6. R-forráskód mutatja, hogy lehet főkomponens-analízist végezni az R statisztikai programban. A főkomponens-analízis esetében kiindulhatunk korrelációs és kovariancia-mátrixból is. A két megoldás nem fog azonos eredményre vezetni, mivel a korrelációs mátrixból kiinduló megoldás az adatok sztenderdizálását jelenti. A 2.6. R-forráskódban a kovariancia-mátrixos megoldást követjük. Ezt akkor érdemes használni, ha a változóink azonos egységben mérhetőek, illetve ha a főkomponens-elemzés után egy új adat főkomponens-értékét szeretnénk meghatározni. Egyéb esetben a korrelációs-mátrixból kiinduló megoldás javasolt. További fontos tudnivaló, hogy az R-ben két alapvető parancssor van a főkomponens-analízis futtatásához. Az egyik a 2.6. R-forráskódon látható  „prcomp” parancs, amely inkább a kovariancia-mátrixból kiinduló megoldást kezeli felhasználóbarátabb módon, míg a másik parancs, a „princomp” inkább a korrelációs mátrix használata esetén javasolt. Ebben a példában most a kovariancia-mátrixos megoldást mutatjuk meg, ám mindenhol hivatkozunk a korrelációs-mátrixos megoldásra is. Konkrét példákat láthatunk a korrelációs-mátrixból kiinduló főkomponens-analízisre a 2.5 példák esetében. Az eredményeket pedig a 2.6. R-eredmény tartalmazza. Az eredményben összesen négy főkomponenst láthatunk, minden egyes oszlop egy főkomponens. Ennek oka, hogy mindig annyi főkomponens lehetséges, ahány változónk van, jelen esetben pedig négy változóval dolgozunk.

Az első sor („Standard deviation”) a főkomponensek sztenderd szórását tartalmazza. A sztenderd szórások azért fontosak, mert a szórás négyzet adja a varianciát. Természetesen lekérhetjük a varianciát is, amely megegyezik a sajátértékkel (2.5. R-forráskód, illetve eredmény).

A 2.6 R-eredmény második sora („Proportion of Variance”) azt mutatja, hogy az adott főkomponens az összvariancia hány százalékát magyarázza. Míg a harmadik sor mutatja („Cumulative Proportion”), hogy az addigi főkomponensek összesen mennyi varianciát magyaráznak. Az első főkomponens az összvariancia 93%-át magyarázza, a második csupán 5%-ot, vagyis az első két variancia összesen 98%-ot magyaráz, ahogyan az az alsó sorban is látszik. A további főkomponensek kevesebb, mint 1%-ot magyaráznak, és a négy főkomponens együtt a teljes varianciát magyarázza.

Korábban volt szó róla, hogy főkomponens-analízisnél az első főkomponens magyarázza az összvariancia legnagyobb részét. Ez most teljesül, hiszen az első főkomponens több mint 90%-át magyarázza az összvarianciának.

Mindezek fényében csupán az első főkomponenst tartjuk meg a négyből. Amiből az következik, hogy az adatok jól illeszkednek egy dimenzióra. Vagyis a négy tantárgy jegyeit jól reprezentálhatjuk egyetlen egy mérőszámmal, amely magába sűríti a matek, fizika, informatika és a kémia jegyeket is.

Az egyes változók „súlyának” vizsgálatához, vagyis az egyes főkomponensek sajátvektorainak vizsgálatához használjuk a 2.7. R-forráskódot, illetve R-eredményt.

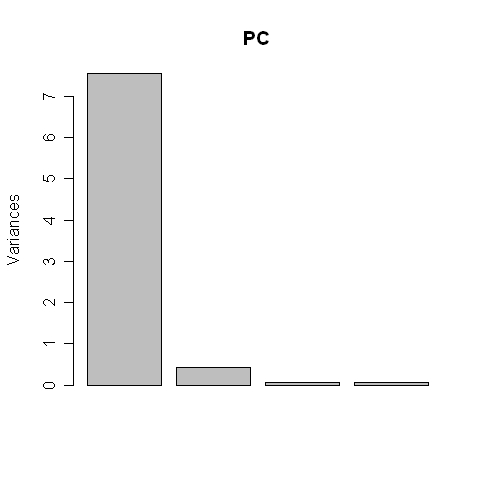
A már korábban említett „princomp” megoldás esetében ezeket a súlyokat a „loadings” paranccsal hívhatjuk elő. Például, ha a parancssor
„fokomp<-summary(princomp(~matek+fizika+informatika+kemia, cor=TRUE))” volt, akkor a „fokomp$loadings” parancssort kell használni.

Az egyes főkomponensekhez tartozó sajátvektorok komponensei azt jelzik, hogy a főkomponensekben az eredeti változók mekkora mértékben járulnak hozzá az egyes főkomponensekhez. Láthatjuk, hogy az első főkomponenst a matek, informatika és a kémia körülbelül egyenlő arányban határozza meg (0,5 körüli értékek), a fizika egy kicsit kisebb hatást fejt ki rá (0,361).  A sajátértékeket és a sajátvektorokat egy másik paranccsal, külön is lekérhetjük (2.5. R-forráskód, illetve eredmény). A 2.5. R-eredményen szereplő sajátvektorok értékei („vectors”) megegyeznek a 2.7. R-eredményen látható értékekkel. Fontos különbség, hogy itt a sajátvektorok mellett az egyes főkomponensek sajátértékei („values”) is szerepelnek. Ez azért hasznos, mert a (sztenderizált változókkal számított) főkomponensek számának meghatározásánál egyik eljárás az, hogy azokat a főkomponenseket tartjuk meg, melyek sajátértéke 1-től nagyobb (ugyanis az eredeti változók sajátértéke egy). Ezt gyakran szokták grafikusan is megjeleníteni, ahogyan az a 2.8. R-forráskódon és eredményen is látszik. A grafikus megjelenítés a 2.5 R-eredményben szereplő sajátértékeket ábrázolja.

               PC1    PC2    PC3    PC4
matek       -0.573  0.134 -0.216  0.779
fizika      -0.361 -0.656 -0.584 -0.315
informatika -0.525  0.653 -0.123 -0.532
kemia       -0.517 -0.354  0.773 -0.104

2.8. R-eredmény.

Végezetül már csak annyi maradt, hogy megnézzük az egyes egyének főkomponens-értékeit. Ezeket az értékeket úgy kapjuk, hogy az eredeti adatokat megszorozzuk a (normalizált) sajátvektor megfelelő komponensének értékeivel. Ha az érdemjegyeiket egyetlen mérőszámmal szeretnénk kifejezni, akkor a főkomponens-érték az, amely a lehető legjobban magában foglalja az egyes tantárgyakból szerzett jegyeket és ezáltal a reál tantárgyak iránti fogékonyság mérőszáma lehet. Ennek kiszámítását a 2.9. R-forráskóddal tehetjük meg. Az eredményeket a 2.9. R-eredmény mutatja. Mivel az egyes változók együtthatói (lásd a sajátvektor első komponensének értékei, 2.7. R-eredmény) negatívak, így a főkomponens értékei minél kisebbek, annál jobb pontszámra utalnak a reál tárgyak iránti fogékonyság tekintetében. Vagyis a legjobban a kilencedik személy teljesít a reál tárgyakból, legrosszabbul pedig a hatodik. Ezek az értékek centralizáltak, vagyis 0 átlagúak. Mindez abból következik, hogy az R úgy számítja ki ezeket az értékeket, hogy először centralizálja az eredeti adatokat (kivonja az egyes változók értékeiből a változók átlagát), majd megszorozza az így kapott centralizált pontszámokat a megfelelő sajátvektor értkeivel.

     PC1     PC2      PC3     PC4
1 -2.075 -0.7114 -0.22236  0.3890
2 -1.502 -0.8451 -0.00604 -0.3904
3  0.825  1.0408 -0.16733 -0.3319
4  2.447 -0.3994  0.29562 -0.0477
5 -2.239  0.5977  0.23822  0.1718
6  4.937  0.1773 -0.32625  0.2280
7 -2.239  0.5977  0.23822  0.1718
8  2.447 -0.3994  0.29562 -0.0477
9 -2.600 -0.0582 -0.34568 -0.1428

A „princomp” parancs esetében főkomponens-értékeket a „scores” parancs segítségével érhetjük el (például „fokomp$scores”).

A kapott eredmények alapján azt is meg tudjuk mondani, hogyan alakul egy adatbázisban nem szereplő személy reál tárgyak iránti fogékonysága, csupán az együtthatókkal kell megszorozni az egyes tantárgyak eredményeit. Tehát ha van valaki, aki matekból 3-as, fizikából 2-es, informatikából 3-as és kémiából 1-es jegyet kapott, akkor a reál tárgyak iránti fogékonyság mérőszáma a következőképpen alakul (ez nem sztenderdizált mérőszám):

[1] 2.745333

Már említettük korábban, hogy a főkomponens-értékeket úgy kapjuk, hogy a sajátvektor értékeit megszorozzuk a centralizált pontértékekkel (ami az átlag kivonását jelenti az egyes pontszámokból). Vagyis, ha ezeket az értékeket ily egyenletként felírjuk (2.10. R-forráskód), akkor az új személy főkomponens-értéke alapján megmondhatjuk, hogy milyen teljesítményt nyújt a vizsgált adatbázis eredményeihez viszonyítva. A 2.10. R-eredmény alapján a személy teljesítménye a többi személy teljestíményéhez viszonyítva gyengének mondható.

Ezen a ponton érdemes egy kicsi kitérőt tenni a főkomponensek varianciája kapcsán. Korábban volt szó róla, hogy a főkomponens-analzis olyan súlyokat keres a változókhoz, amelyek segítségével készített összmutató információtartalma - vagyis varianciája - maximális lesz. A 2.5. R-eredményen láthattuk, hogy az első főkomponens varianciája 7,547 kerekítve. A használt együtthatókat a 2.7. R-eredmény mutatja. De mi történik, ha más együtthatókat használunk? A variancia csökkeni fog. Ezt természetesen nem tudjuk minden egyes eltérő értékre megmutatni, de illusztrációként nézzünk egy olyan példát, ahol az együtthatók a következőképpen alakulnak:

Ekkor az együtthatókra teljesül az a feltétel is, hogy négyzetösszegük 1. Most készítsük el az R-ben ezeket az együtthatókat, majd számítsuk ki az így kapott főkomponens-értékek varianciáját (2.11. R-forráskód) a 2.1. R-forráskóddal bevitt adatokra. A 2.11. R-forráskód a következőképpen épül fel. Az első négy paranccsal centralizáljuk az eredeti adatokat (változók átlagát kivonjuk az egyes változók értékeiből). Ezt követően kiszámítjuk az egyes együtthatókat és a főkomponens-értéket, majd pedig ezek szórásnégyzetét, vagyis varianciáját.

[1] 6.92

A 2.11. R-eredményen láthatjuk az ily módon kapott összpontszám varianciáját, amely lényeges kisebb, mint a főkomponens varianciája, vagyis a főkomponens-analízissel történő adatösszegzés sikeresebb volt az információmegtartás szempontjából.

     matek fizika informatika  kemia
[1,] -0.99 -0.906      -0.955 -0.977

A 2.12. R-forráskód segítségével egy úgynevezett komponens-mátrixot hívhatunk elő (például az SPSS-ben ezt főkomponens-súlynak nevezik). Ugyanezt a parancssort a „princomp” parancssoros  eljárás esetében a következő formában írhatjuk be „print(cor(PC$scores[,1], d),digits=3)”. A komponens mátrix az első főkomponensbeli főkomponensértékek és az eredeti változó értékei közötti korrelációt mutatja. A magas korrelációs értékek arra utalnak, hogy az első főkomponens értékei jól tudják visszaadni az eredeti adatokat, vagyis a modell jól illeszkedik. A 2.12. R-eredményen láthatjuk, hogy a korrelációs értékek magasak. A negatív előjelet most figyelmen kívül hagyhatjuk, hiszen ezek abból adódnak, hogy a 2.7. R-eredményen szereplő első főkomponensbeli főkomponenssúlyok értéke negatív. Gyakran előfordul, hogy ezek az előjelek különböző statisztikai programok használata esetén eltérnek, ám abszolút értékük azonos, ugyanazokat a főkomponenseket kapjuk. Ez mindig az adott szoftver programozási sajátosságaiból adódik. Láthatjuk, hogy a matek változót tudta a legjobban becsülni a modell (0,99), legkevésbé pedig a fizikát (0,906).

A 2. Interaktív illusztrációval érzékeltetjük az első főkomponens „ideális” tulajdonságait.