|
2.5 Példák
2.5.1 Probléma: Létezik a reál tárgyak iránti fogékonyság?
A 2.2. táblázat adatai alapján már foglalkozunk azzal a felvetéssel, hogy néhány tantárgy eredményeit egyetlen mérőszámmal reprezentáljuk. Korábbi példánkban a matematika, fizika, informatika és kémia jegyek közötti összefüggéseket vizsgáltuk egy kisebb adatbázison, hogy áttekinthetően követhessük a főkomponens-analízis lépéseit.
Az első példában ugyanezt a jelenséget járjuk körbe, de ezúttal a főkomponens-analízis mintanagysággal szemben támasztott követelményének is eleget teszünk, egy sokkal nagyobb adatbázis segítségével mutatjuk be, hogyan végezhetünk főkomponens-analízist az R statisztikai program segítségével.
Első lépésben vegyük szemügyre az adatbázist, hívjuk be az adatokat (2.15. R-forráskód és R-eredmény).
d<-read.csv("c:/adat/jegy.csv")
print(d)
|
| |
2.15. R-forráskód
|
matek fizika informatika kemia
1 5 5 4 5
2 4 5 4 5
3 3 3 4 3
4 2 3 2 3
5 5 4 5 5
6 1 2 1 1
7 5 4 5 5
8 2 3 2 3
9 5 5 5 5
10 5 3 4 5
11 4 5 4 5
12 3 3 4 3
13 2 3 2 3
14 5 4 4 5
15 1 2 1 1
16 5 4 5 3
17 2 3 2 3
18 5 5 5 5
19 5 5 4 5
20 4 5 4 5
21 3 3 4 3
22 2 3 2 3
23 5 3 5 5
24 1 2 2 1
25 5 4 5 5
26 2 3 2 3
27 5 5 5 5
28 5 4 5 5
29 2 3 2 3
30 5 4 5 5
|
| |
2.15. R-eredmény.
|
Ha a 2.15. R-eredményt nézzük, akkor láthatjuk, hogy a négy tantárgy jegyei viszonylag összhangban vannak egymással abban az értelemben, hogy azok a diákok, akik az egyik tárgyból jól teljesítenek, azok a másik három tárgyból is. Ugyanez igaz azokra is, akik az egyik tantárgyból gyengébben teljesítenek. Például az 1-es sorszámmal jelzett tanuló jelest kapott mindenből, kivéve informatikából, amiből négyest szerzett. A 6-os sorszámmal jelzett tanuló pedig fizika kettesen kívül minden más tantárgyból elégtelent kapott.
Ezek alapján van egy olyan sejtésünk, hogy egy úgynevezett reál tárgyak iránti fogékonyság mutatóval reprezentálhatjuk a négy tantárgy eredményeit. Vagyis főkomponens-analízis segítségével ellenőrizhetjük (2.16. R-forráskód), hogy az adatok valóban jól sűríthetőek-e egyetlen dimenzióba vagy mérőszámba, és ha igen, akkor ezt a dimenziót elnevezhetjük reál tárgyak iránti fogékonyságnak.
PC<-summary(princomp(d))
PC
|
| |
2.16. R-forráskód
|
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 2.4689301 0.67105532 0.44031767 0.27922605
Proportion of Variance 0.8940766 0.06605015 0.02843737 0.01143587
Cumulative Proportion 0.8940766 0.96012677 0.98856413 1.00000000
|
| |
2.16. R-eredmény.
|
A 2.16. R-eredmény alapján az első főkomponens magyarázza az összvariancia majdnem 90%-át („Proportion of Variance 0.89”). A második, harmadik és negyedik főkomponens csak 7°%, 3%, illetve 1%-ot magyaráz. Ez alapján csak az első főkomponenssel dolgozunk tovább, hiszen a többi főkomponens magyarázóértéke elhanyagolhatóan kicsi.
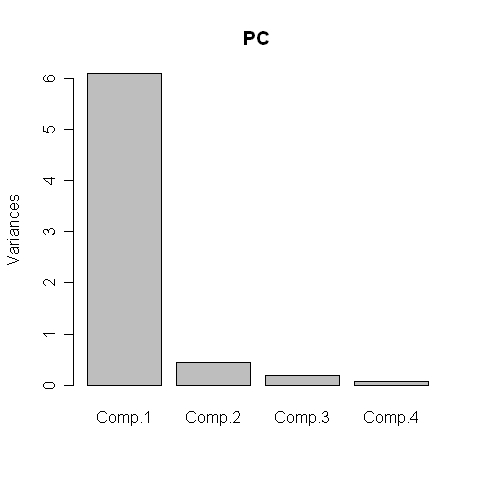
Ugyanerre az eredményre jutunk, ha grafikusan megjelenítjük az egyes főkomponensek sajátértékeit (2.17. R-forráskód), és csak az egynél nagyobb sajátértékű főkomponenseket vesszük figyelembe (2.17. R-eredmény).
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
matek 0.596 -0.231 0.152 0.754
fizika 0.334 0.631 -0.696
informatika 0.519 -0.587 -0.335 -0.523
kemia 0.513 0.451 0.616 -0.392
Comp.1 Comp.2 Comp.3 Comp.4
SS loadings 1.00 1.00 1.00 1.00
Proportion Var 0.25 0.25 0.25 0.25
Cumulative Var 0.25 0.50 0.75 1.00
|
| |
2.18. R-eredmény.
|
|
cor<-cor(PC$scores[,1], d)
print(cor, digits=3)
|
| |
2.19. R-forráskód
|
matek fizika informatika kemia
[1,] 0.984 0.845 0.945 0.949
|
| |
2.19. R-eredmény.
|
Végezetül a 2.18. R-forráskódhoz tartozó 2.18. R-eredményből megállapíthatjuk az egyes változók relatív fontosságát az első főkomponens szempontjából. A sajátvektorok komponensei alapján az első főkomponenst döntően a matematika, informatika és kémia eredmények határozzák meg. A fizika tantárgyból elért teljesítmény valamivel kisebb mértékben járul hozzá ehhez a főkomponenshez.
A 2.19. R-eredményen látható komponens mátrix adatai is alátámasztják azt, hogy az első főkomponens jól magába tömöríti egyes eredeti változókban szereplő adatokat, hiszen a korrelációs értékek igen magasak. A matek változót tudta a legjobban becsülni a modell (0,98), legkevésbé pedig a fizikát (0,85).
library(Rcmdr)
cov<-cov(d)
rel<-reliability(cov)
print(rel, digits=3)
|
| |
2.20. R-forráskód
|
Alpha reliability = 0.947
Standardized alpha = 0.951
Reliability deleting each item in turn:
Alpha Std.Alpha r(item, total)
matek 0.907 0.916 0.953
fizika 0.959 0.960 0.800
informatika 0.928 0.940 0.882
kemia 0.918 0.926 0.911
|
| |
2.20. R-eredmény.
|
cor<-cor(d)
eigen<-eigen(cor)$value
theta<-length(g)/(length(g)-1)*(1-1/eigen[1])
print(theta,digits=3)
|
| |
2.21. R-forráskód
|
A 2.20. R-forráskóddal egy Cronbach-alfa mutatót kértünk az adatokra, míg a 2.21. R-forráskóddal egy Thetát. Jóllehet, most nem itemszelekciót végzünk, ez a két mutató informatív lehet a tekintetben, hogy mennyire egydimenziósak az adatok. A Cronbach-alfa értéke 0,947 (2.20. R-eredmény), míg a Theta 0,952 (2.21. R-eredmény). Mindkét mutató igen magas, egyhez közeli értéket mutat.
Összességében az adatok jól sűríthetők egyetlen mérőszámba, minimális információveszteséggel, ezt a mutatót pedig hívhatjuk a reál tárgyak iránti fogékonyság mutatójának.
|