1.2.6 Négyzetes korrelációs együttható

A valóságban gyakran előfordul, hogy egyes jelenségek együtt járnak, közösen fordulnak elő, együtt változnak anélkül, hogy bármi ok-okozati összefüggés lenne köztük. Ilyen lehet például a mentális megbetegedések száma és az áremelések közötti kapcsolat. Minél nagyobb mértékű az áremelkedés, annál több a mentális megbetegedések száma. Abszurd lenne azt feltételezni, hogy például a gázár és a mentális egészség között bármi ok-okozati kapcsolat van. Ám mégis megfigyelhető, hogy együtt, egy irányban mozognak. Ennek oka természetesen nem misztikum, hanem például az áremelkedésekkel járó stressz.

Van tehát két változó, melyek között látszólag semmi ok-okozati összefüggés nincs, mégis észlelhető a kapcsolat köztük. Ez a kapcsolat a nagyon szorostól, amikor szinte egy a két változó, a nagyon laza kapcsolatig terjedhet, amikor szinte már nem is érzékeljük az összefüggést. Hogy pontosabban meg tudjuk határozni ennek a mértékét, szükséges valamilyen mérőszámot használni, ez a Pearson-féle korrelációs együttható.

A Pearson-féle korrelációs együttható (${\text{r}}_{\text{XY}}$) az X és az Y változó közötti összefüggés erősségét mutatja. Minél nagyobb az ${\text{r}}_{\text{XY}}$ abszolút értéke, annál szorosabb az összefüggés az X és az Y változó között. Például ha ${\text{r}}_{\text{XY}}$ = 0,1, akkor az a kapcsolat nagyon laza, míg egy ${\text{r}}_{\text{XY}}$ = -0,89 korrelációs érték már egy igen szoros, de negatív irányú kapcsolatra utal. A statisztikában jártas olvasók tudhatják, hogy a korreláció együttható és a legkisebb négyzetek egyenese között a következő kapcsolat áll fent (levezetés az 1.7.4 mellékletben található):

ahol ${\sigma }_X$  és ${\sigma }_Y$ X illetve Y változó sztenderd szórása.

Ha a korrelációs együtthatót a négyzetre emeljük ($r_{XY}^2$), akkor megkapjuk, hogy Y varianciájának mekkora hányadát magyarázza X varianciája, vagy fordítva, X varianciájának mekkora hányadát magyarázza Y varianciája.

Az X és az Y változó értékei az adott skálának megfelelően változhatnak. Ezt a variabilitást a sztenderd szórás (${\sigma }_X$  és ${\sigma }_Y$), vagy a variancia jellemzi (${\sigma }_X^2$  és ${\sigma }_Y^2$). Az mind az X, mind az Y variabilitását két tényező okozhatja:

• adatbázist alkotó személyek közötti különbségek, amelyekre már előre számítunk
• random hiba.

Így a korrelációs együtthatóra tekinthetünk úgy, mint az az arány, amely számszerűleg kifejezi X és Y közös variabilitását vagy kovarianciáját, és a nevezője X és Y teljes lehetséges varianciáját mutatja. Ha ezt az együtthatót a négyzetre emeljük, akkor egy variancia arányt kapunk, amely számlálójában X és Y közös varianciája szerepel, nevezőjében pedig a teljes variancia (1.4. egyenlet):

Az 1.1/B táblázat és a 1.18. R-eredmény adatai alapján a megfelelő értékeket behelyettesítve:

Ezt a számítást is könnyedén elvégezhetjük az R program segítségével, az 1.19. R-forráskódnak megfelelően.

[1] 0.9995596

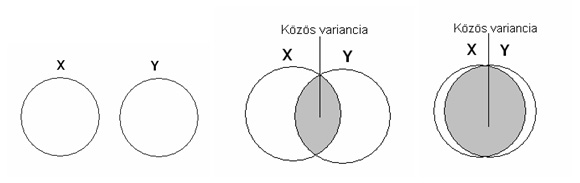
Az arányt legtöbbször százalékos formában adjuk meg, vagyis adataink esetében 99%-ban lehet a függő változó varianciáját magyarázni.

Az 1.9. ábra a magyarázott varianciát koncepcióját szemlélteti. Az X-szel jelölt kör az X változó értékeinek a varianciáját, az Y-nal jelölt kör az Y változó értékeinek a varianciáját szemlélteti. Minél nagyobb a két kör közös területe,

• annál nagyobb X és Y közös varianciája
• annál nagyobb Y-beli varianciaszázalékot magyaráz X
• annál nagyobb X-beli varianciaszázalékot magyaráz Y.

Például a baloldali két körnek azért nincs közös területe, mivel nincs közös varianciája a két változónak, vagyis a két változó független egymástól ($r_{XY}^2$=0). A középső ábrán már van valamennyi átfedés a két kör között, a két változónak van egy közepes mennyiségű közös varianciája, vagyis a két változó közepes mértékben jósolható meg egymásból ($r_{XY}^2$=0,5). Végül a harmadik ábra egy egészen szoros kapcsolatot mutat, itt majdnem a teljes varianciát magyarázzák a változók, hiszen $r_{XY}^2$=0,96.

1.9. ábra. A magyarázott variancia koncepciója.