1.2.4 A lineáris regressziós modell

Az előzőekben már volt szó róla, hogy a lineáris kapcsolatot egy egyenes írja le, melynek egyenlete a már ismert 1.1. egyenlet:

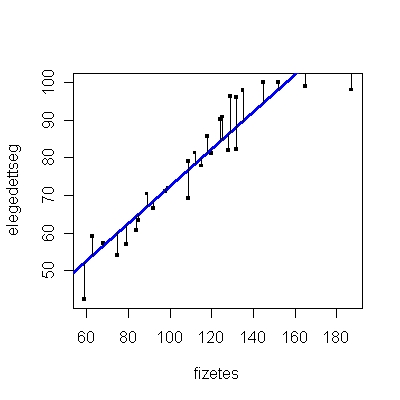
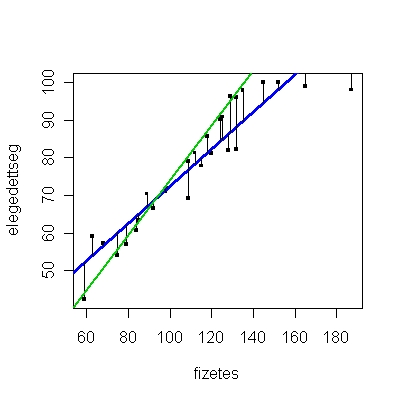
A probléma abból adódik, hogy amint az 1.5. ábrán is látható, a pontok az esetek többségében nem egy egyenesre esnek, így nem teljesen világos, hogy hogyan határozzuk meg $b_0$-t és $b_1$-et. Vagyis számtalan olyan egyenes lehet, amelyet a ponthalmazra (a személyek adatainak a halmazára) illesztünk, és el kell döntenünk, hogy a számtalan egyenes közül melyik a „legjobb”, vagyis melyik illeszkedik a legjobban az adatokra. Kérdés lehet, hogy egyáltalán létezik-e ilyen egyenes, és valóban csak egy darab van-e belőle, nem lehet, hogy több egyenes is jó lehet?

Ezt a problémát úgy lehet megválaszolni, hogy meghatározunk néhány kritériumot, amelyeknek teljesülniük kell, amikor $b_0$-t és $b_1$-et becsüljük, és meghatározzuk azokat a $b_0$  és $b_1$  értékeket, amelyek teljesítik ezeket a kritériumokat. Az egyik legismertebb és legelterjedtebb ilyen kritérium a legkisebb négyzetek elve. Ez a kritérium azt állítja, hogy úgy kell $b_0$-t és $b_1$-et meghatározni, hogy a megfigyelt (Y) célváltozó és annak becsült ($\widehat{Y}$) értékei közötti eltérés minimális legyen.

A módszert azért hívják a legkisebb négyzetek elvének, mert az egyenest úgy illesztjük a ponthalmazra, hogy az egyenes és pontok közötti eltérések négyzetének összege [azaz ${\displaystyle \sum (Y}-\stackrel{⌢}{Y}{)}^2$] minimális legyen. Ez az elv garantálja azt, hogy tényleg van egy ilyen egyenes, és azt is, hogy csak egyetlen egy darab van. Az 1.8. ábrán a legkisebb négyzetek elvével illesztett egyenes (kék színnel jelzett) mellé illesztettünk egy másik egyenest is (zöld színnel jelzett). Szemmel is látható, hogy bár alig tér el a két egyenes egymástól, a nem a legkisebb négyzetek elvével illesztett egyenes lényegesen távolabb van a legtöbb ponttól, mint a legkisebb négyzetek elvével illesztett egyenes. A legkisebb négyzetek elvéről részletesen az 1.7.1 mellékletben van szó.

A legkisebb négyzetek elve tehát az a módszer, amellyel a regressziós egyenlet együtthatóit, vagyis $b_0$-t és $b_1$-et becsüljük. Ebből következik, hogy a kapott együtthatók nem a valódi, mért adatok együtthatói, azokat ugyanis nem ismerjük. Ellenben nagyon jó becslést tudunk rájuk adni a fent bemutatott elv alapján. Az együtthatókból a regressziós egyenlet segítségével visszaszámolhatjuk az „eredeti” adatokat, vagyis megnézhetjük, hogy az ismert független változóhoz az egyenlet alapján milyen függő változóbeli értékek tartoznak. Továbbá, mivel az adatok, a pontok, nem az elméleti egyenesre esnek, vagyis az Y valódi értékei eltérnek a $b_0$ és $b_1$ segítségével becsült értékektől, így ezzel a különbséggel számolni kell, ez a statisztikai értelemben vett hiba ($\epsilon$). Ily módon a lineáris regresszió egyenletét a következőképpen egészítjük ki (1.2. egyenlet):

Ahol $b_0$  és $b_1$ már ismert, $\epsilon$ pedig az X változótól független hiba.

1.7. ábra. A legkisebb négyzetek egyenese. Az 1.17. R-forráskód alapján.

1.8. ábra. A legkisebb négyzetek elve. Kék színnel a legkisebb négyzetek elvével illesztett egyenes, zölddel pedig egy másik egyenes látható.

Az 1. Interaktív illusztrációval érzékeltetjük a regressziós egyenes „ideális” tulajdonságait.

A legkisebb négyzetek elvénél tulajdonképpen ezt a hibát minimalizáljuk, hogy minél pontosabb becslést kapjunk.

Az 1.1/B táblázat egy kisebb adatbázist tartalmaz, melyben a fizetés nagysága és a munkahellyel való elégedettség szerepel. A 1.2. ábrán láthattuk, hogy kapcsolatuk egy egyenessel jellemezhető, lineáris kapcsolat. Ez azt jelenti, hogy lineáris regresszió-analízissel ezekre az adatokra kiszámolhatjuk a regressziós együtthatók becsléseit. A képletek levezetése és a számolás megtalálható az 1.7.1 mellékletben. De ugyanazt a számolás elvégezhetjük az R-ben is természetesen (1.18. R-forráskód).

Call:
lm(formula = `elégedettség` ~ `fizetés`)
Coefficients:
(Intercept)    `fizetés`  
      3.211        0.628

A becsült együtthatók az 1.18. R-eredmény alapján: $b_1$=0,628 és $b_0$=3,211. A regressziós egyenlet pedig:

elégedettség = 3,211+ 0,628 * fizetés