|
1.2.3 Lineáris (egyenes) kapcsolat jellemzése
Az egyik legegyszerűbb szisztematikus kapcsolat formája az egyenes. Ha egyenesről beszélünk, akkor szükséges lenne pontosan megadni, hogy milyen az az egyenes, amelyről szó van. Egyértelmű megadásuk az úgynevezett koordináta-rendszerhez kötött, amelyben az egyenesnek két gyakori megadási módja ismert:
a) megadhatunk két egyenesen fekvő pontot, vagy
b) megadhatjuk az egyenes egy pontját és az egyenes meredekségét.
Ezek közül a második megadási forma a legelterjedtebb, ahol az egyenes egyik pontját az Y tengellyel való metszéspontja adja. Az egyenes metszéspont-meredekség egyenletét a következőképpen adhatjuk meg (1.1. egyenlet):
(1.1. egyenlet)
ahol
az egyenes y-tengellyel való metszéspontja
a meredekség.
Az egyenes Y tengellyel való metszéspontja az Y-nak az az értéke, amit X = 0-nál vesz fel. A meredekség pedig az a szám, ami megmutatja, hogy X egységnyi emelkedése hány egységnyi emelkedést eredményez Y értékeiben. Az 1.5. ábra egyenesének az adataira is kiszámíthatjuk a meredekséget és a tengelymetszetet az R segítségével. Ehhez először jelenítsük meg az adatokat az 1.11. R-forráskóddal, majd számítassuk ki a programmal a szükséges értékeket (1.12. R-forráskód).
d<-read.csv("c:/adat/elegedettseg.csv")
print(d, digits=1)
|
| |
1.11. R-forráskód
|
fizetes elegedettseg kor nem
1 109 69 20 nő
2 125 91 46 férfi
3 98 71 36 nő
4 124 90 46 férfi
5 115 78 31 férfi
6 132 96 49 férfi
7 124 90 46 férfi
8 99 72 37 nő
9 165 99 49 férfi
10 187 98 32 férfi
11 152 100 49 férfi
12 132 82 21 férfi
13 128 82 25 férfi
14 118 86 44 férfi
15 112 81 41 férfi
16 89 70 45 nő
17 68 57 42 nő
18 59 42 22 nő
19 75 54 28 nő
20 63 59 51 nő
21 85 63 35 nő
22 79 57 29 nő
23 84 61 31 nő
24 92 67 34 nő
25 109 79 40 férfi
26 118 86 44 férfi
27 129 96 53 férfi
28 135 98 49 férfi
29 145 100 47 férfi
30 120 81 32 férfi
|
| |
1.11. R-eredmény.
|
lm<-lm(elegedettseg~fizetes, data=d)
print(lm,digits=1)
|
| |
1.12. R-forráskód
|
Call:
lm(formula = elegedettseg ~ fizetes, data = d)
Coefficients:
(Intercept) fizetes
23.1 0.5
|
| |
1.12. R-eredmény.
|
A 1.12. R-eredményen látható „intercept” értéke vonatkozik a metszéspontra, vagyis
=23,1. A fizetéshez tartozó értékek pedig az egyenes meredekségének az értéke, azaz
=0,5. Ekkor a függvényszerű kapcsolatot az elégedettség = 23,1 + 0,5 * fizetés képlet írta le.
A 1.6. ábra különböző meredekségeket ábrázol. Az egyes ábrák felett látható az R parancssor is, amivel az adott ábrát létre lehet hozni. Az adatokat és az első ábra forráskódját az 1.13. R-forráskód tartalmazza.
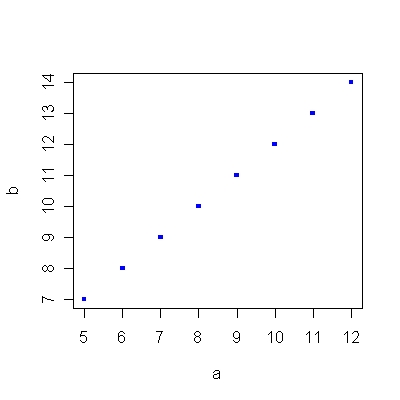
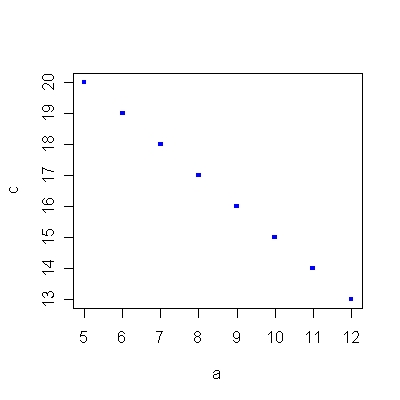
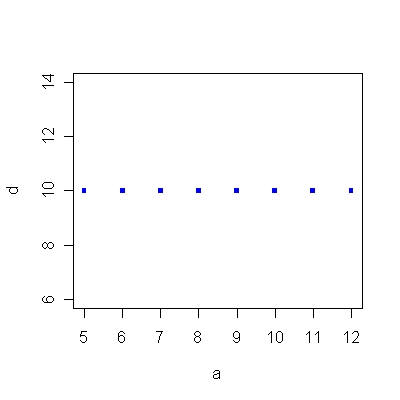
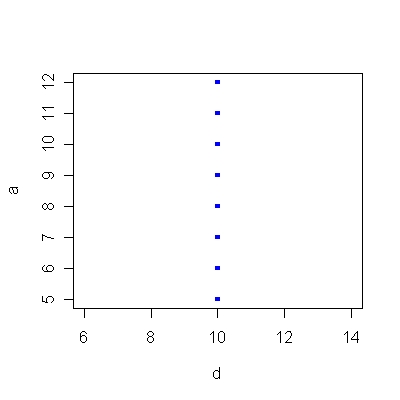
Az 1.6/A ábra azt az esetet mutatja, amikor az X változóval együtt nő az Y változó, ez egy pozitív meredekség. Az 1.6/B ábrán már az X növekedése csökkenést eredményez az Y változóban, ez negatív meredekség. Az 1.6/C ábra a nulla meredekséget mutatja, ami a két változó közötti függetlenséget jelzi: az X bármely értéke esetén Y értéke 10. Végül az 1.6/D ábra azt az egyenest mutatja, melynek nem értelmezhető a meredeksége, mivel X változóban nincs változás.
a=c(5,6,7,8,9,10,11,12)
b=c(7,8,9,10,11,12,13,14)
c=c(20,19,18,17,16,15,14,13)
d=c(10,10,10,10,10,10,10,10)
plot(b~a, cex=5, pch=".", col=4)
|
| |
1.13. R-forráskód
|
|
plot(c~a, cex=5, pch=".", col=4)
|
| |
1.14. R-forráskód
|
| |
1.6/A ábra. Az 1.13. R-forráskód alapján.
|
| |
1.6/B ábra. Az 1.14. R-forráskód alapján.
|
|
plot(d~a, cex=5, pch=".", col=4)
|
| |
1.15. R-forráskód
|
|
plot(a~d, cex=5, pch=".", col=4)
|
| |
1.16. R-forráskód
|
| |
1.6/C ábra. Az 1.15. R-forráskód alapján.
|
| |
1.6/D ábra. Az 1.16. R-forráskód alapján.
|
|