|
1.6.4 probléma. Hogyan alakul a betanított munkások teljesítménye a munka megismerésétől kezdődően az idő előre haladtával?
Mindennapos jelenség, hogy amikor a betanított munkások egy új munkával ismerkednek, akkor kezdetben gyengébben teljesítnek, majd egy idő után ugrásszerűen megnő a teljesítményük. Hogyan tudjuk ezt megvizsgálni a lineáris regresszió keretein belül? Első lépésként hívjuk be az adatokat a következő parancssorral (1.39. R-forráskód):
d<-read.csv("c:/adat/betanitott.csv")
print(d)
|
| |
1.39. R-forráskód
|
d1 d2 proba darab
1 1 0 12 0
2 1 0 12 1
3 1 0 14 2
4 1 0 14 3
5 1 0 14 2
6 1 0 16 19
7 1 0 16 5
8 1 0 16 15
9 1 0 18 26
10 1 0 18 31
11 1 0 20 52
12 1 0 20 41
13 1 0 20 38
14 1 0 20 42
15 1 0 22 65
16 1 0 22 39
17 1 0 24 78
18 1 0 24 69
19 1 0 24 71
20 0 1 26 145
21 0 1 26 155
22 0 1 26 152
23 0 1 28 220
24 0 1 28 225
25 0 1 28 233
26 0 1 30 310
27 0 1 30 298
28 0 1 30 318
29 0 1 30 304
30 0 1 25 118
31 0 1 25 109
32 0 1 26 156
33 0 1 30 315
34 0 1 31 398
35 0 1 32 382
36 0 1 37 589
37 0 1 32 381
38 0 1 31 341
|
| |
1.39. R-ererdmény.
|
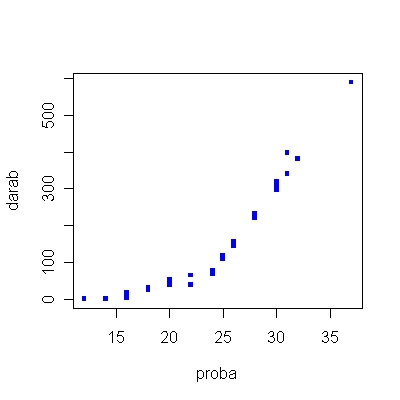
Elsőként vegyük alaposan szemügyre az adatainkat. A „proba” változó a próbák számát jelenti a munkavégzés betanulása során, míg a „darab” változó a teljesítményt méri darabszámban. Hogy tisztább képet kapjunk a helyzetről, kérjünk egy pontdiagramot az adatainkról (1.40. R-forráskód).
|
plot(darab~proba, data=d, pch=".", cex=5, col=4)
|
| |
1.40. R-forráskód
|
|
1.12. ábra. A próbák számának és a darabszámban mért teljesítménynek a kapcsolata.
Az 1.53. R-forráskód alapján.
|
A 1.12-es ábrát vizsgálva észrevehetjük, hogy a 24. próba környékén egy jelentős ugrás következik be a teljesítményben. Hogy ez az ugrás valóban létezik, vagy csak annak tűnik, arra ad választ a szegmentált regresszió-számítás.
Mivel a 24. próbánál következik be a jelentős változás, így legyen a „proba” változó 24-es értéke az úgynevezett küszöbérték. A dummy változók már készen szerepelnek az adatbázisban, d1 és d2 jelöli őket. A d1 változó értéke - szegmentált regresszió-számítás elvének megfelelően - 1, ha a „proba” változó értéke 24, vagy annál kisebb, és 0 minden más esetben. A d2 változó ezzel ellentétesen alakul: értéke 0, ha a „proba” változó értéke 24, vagy annál kisebb, és 1 minden más esetben.
A szegmentált regresszió-analízisben először ki kell számolnunk az egyes szegmenseknek megfelelően az együtthatókhoz tartozó változókat. Az 1. szegmens változója az 1.29. egyenlet alapján d1*proba+d2*24, míg a 2. szegmens változója -d2*24+d2*proba lesz. Ezeket a számításokat az R-ben is elvégezhetjük (1.54. R-forráskód):
b1=d$d1*d$proba+d$d2*24
b2=-d$d2*24+d$d2*d$proba
|
| |
1.41. R-forráskód
|
Most már csak le kell futtatnunk a regresszió-számítást a b1 és a b2 változókra (1.42. R-forráskód).
|
print(summary(lm(d$darab~b1+b2)),digits=3)
|
| |
1.42. R-forráskód
|
Call:
lm(formula = d$darab ~ b1 + b2)
Residuals:
Min 1Q Median 3Q Max
-17.85 -5.36 -1.23 4.69 47.25
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.451 10.396 -8.41 6.4e-10 ***
b1 6.559 0.524 12.52 1.7e-14 ***
b2 40.112 0.642 62.51 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.7 on 35 degrees of freedom
Multiple R-Squared: 0.995, Adjusted R-squared: 0.995
F-statistic: 3.57e+03 on 2 and 35 DF, p-value: <2e-16
|
| |
1.42. R-eredmény. A szegmentált regresszió-számítás eredménye.
|
A 1.42. R-eredményen láthatjuk, hogy mindkét változó együtthatójának értéke szignifikáns, és maga a modell is, vagyis valóban létezik az ábrán látható „ugrás” a munkások teljesítményében, a 24. próbától kezdve a teljesítményük óriási léptekben javul, hiszen amíg az első 24 próbában átlagosan b1=6,559 darabot tudnak elkészíteni, addig a 24. hónap után ez az átlag 40,112-re ugrik (b2=40,112). Az R-négyzet értéke 0,995, ami azt mutatja, hogy a modell magyarázóérzéke igen jó.
|