1.2 Egyszerű lineáris regresszió
1.2.1 Milyen mértékű elégedettséget von maga után a fizetésemelés?

Vizsgáljuk a munkahellyel való elégedettséget a fizetés függvényében. Az egyszerűség kedvéért vegyük csak 5 ember adatait. Az adatokat  - melyek teljes mértékben hipotetikusak - az 1.1/A illetve az 1.1/B táblázat tartalmazza.

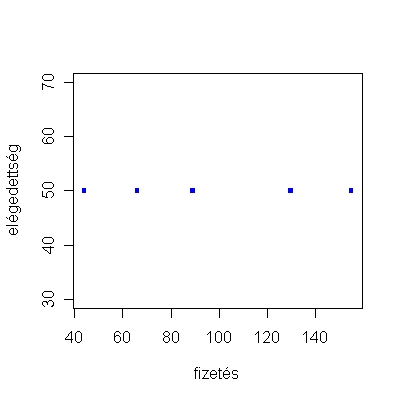
Nézzük először az 1.1/A táblázatban szereplő adatokat. Láthatjuk, hogy az egyes emberek fizetése változatosan alakul, az öt ember fizetése 44 ezer és 155 ezer forint között változik. Ezzel ellentétben a munkahellyel való elégedettség mind az 5 embernél egyforma mértékű, vagyis mindenki egy ugyanolyan átlagos értéket adott egy 1-100-as skálán.

Ha a munkahellyel való elégedettséget szeretnénk becsülni a fizetés nagysága alapján, akkor jó kiindulási pontnak tűnik a két változó pontdiagramjának vizsgálata. Kisebb probléma a pontdiagramokkal, hogy értelmezése - akár a tintafoltoké - az egyéntől függ.

Hogy elkerüljük ezt a potenciális többértelműséget, szükség van arra, hogy szisztematikusan elemezzük az ábrát, meghatározzuk azokat a faktorokat, amelyek felelősek a két változó közötti kapcsolat irányáért és a kapcsolat szorosságáért. Két ilyen fontos faktor van. Az egyik a pontdiagram meredeksége, a másik pedig annak mértéke, hogy mennyire közel vannak az ábrán az eseteket jelző pontok a meredekséget mutató egyeneshez. A lineáris regressziós elemzésben ezt a két mutatót számítjuk ki a változók kapcsolatának jellemzésére.

Ha az adatokat grafikusan szeretnénk megtekinteni, akkor azt könnyedén megtehetjük az R statisztikai program segítségével. Először az 1.1/A táblázatban látható adatokat kell bevinnünk, a következő parancssorokkal (1.1. R-forráskód):

Ezzel a két parancssorral megadtuk a programnak, hogy milyen adatokkal szeretnénk dolgozni. Ennek birtokában már egy pontdiagramot is kérhetünk a két változó közötti kapcsolatról, vagyis megnézhetjük grafikusan, hogy miként alakul a fizetés és munkahellyel való elégedettség kapcsolata. Az ábrakészítéshez tartozó parancssor az R-ben a következő (1.2. R-forráskód):

Az 1.2 forráskóddal nemcsak azt adtuk meg, hogy mely változókat ábrázoljuk, hanem információt adtunk a programnak arról is, hogy milyen szimbólummal ábrázolja az egyes eseteket (ez a pch parancs), mekkora legyen a szimbólumok mérete (cex parancs), valamint a színe (col parancs). Az eredmény az 1.1. ábrán látható. A vízszintes tengely képviseli a fizetés nagyságát, míg a függőleges a munkahellyel való elégedettség mértékét. Láthatjuk, hogy a pontok egy vízszintes egyenesre illeszkednek, hiszen az elégedettség mind az 5 személynél ugyanolyan értékű volt.

1.1. ábra. A fizetés nagysága (ezer) és a munkahellyel való elégedettség kapcsolata az 1.1/A táblázat adatai alapján.

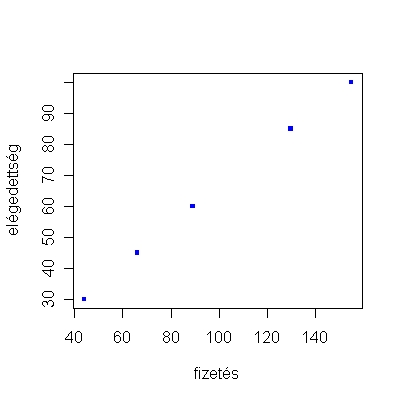
Ha becslést szeretnénk adni arra, hogyan alakul egy olyan ember munkahellyel való elégedettsége, aki nem szerepel ugyan az adatbázisban, de minden másban hasonlít az adatbázisban szereplő személyekhez, akkor azt viszonylag nagy biztonsággal megtehetjük. Becslésünk - további ismeretek hiányában - egy ugyanolyan átlagos 50-es érték lenne, mint amilyen a valamennyi vizsgált személyé. Továbbá teljesen mindegy az, hogy mekkora a személy fizetése, 89 ezer vagy csak 52 ezer, ez a becsült elégedettségi érték a fizetés nagyságától függetlenül 50 lesz.

Mi történik, ha ugyanezt az 1.1/B táblázat adataira nézzük? Ha a táblázat adatait vizsgálgatjuk, akkor azt látjuk, hogy magasabb fizetéshez minden esetben nagyobb elégedettségi szint tartozik. A legalacsonyabb fizetéshez tartozik a legalacsonyabb elégedettségi szint (44 ezer forint és 30-as elégedettségi érték), illetve a legmagasabb fizetéshez a legnagyobb elégedettségi szint (155 ezer forint és 100-as elégedettségi szint). A többi érték a kettő között helyezkedik el, s bármely két személy esetén nézzük, ha egyiknek nagyobb a fizetése, akkor elégedettebb a munkahelyével is. Nézzük meg ismét grafikusan, az adatokat, hogy mit láthatunk egy ilyen adatokból készült ábrán. Most is először az adatokat kell bevinnünk. Az 1.3. R-forráskód megegyezik az 1.1. R-forráskóddal, egyetlen különbség, hogy az elégedettséghez most az 1.1/B táblázat adatait visszük be.

Ezután az ábrakérés teljesen ugyanaz (1.4. R-forráskód), ahogyan az 1.2. forráskódnál le van írva. Az 1.2. ábra mutatja a kapott ábrát.

1.2. ábra. A fizetés nagysága (ezer) és a munkahellyel való elégedettség kapcsolata az 1.1/B táblázat adatai alapján.

Az adatok itt is egy egyenesre illeszkednek, de most ez az egyenes nem vízszintes, hanem valamekkora emelkedést mutat. Ez alátámasztja azt az észrevételünket, hogy magasabb fizetéshez magasabb elégedettség tartozik, vagyis minél többet keres valaki, annál elégedettebb munkahelyével.

Most hogyan tudnánk becsülni egy adatbázisban nem szereplő személy adatait? Ebben az esetben is a vizsgált személyek adatait kell megnéznünk. Már megállapítottuk, hogy minél magasabb valakinek a fizetése, annál elégedettebb munkahelyével, ezért további ismeretek hiányában érdemesnek tűnik a fizetés alapján becsülni az elégedettséget. Próbáljuk megvizsgálni, hogyan alakul pontosan ez a „minél ... annál ...” kapcsolat. Mivel a vizsgált változók értékei egyenletes növekedést mutatnak, és egyenessel jellemezhetőek, bármely két ember adatának vizsgálata ugyanazt az eredményt kell adja a változás mértékének vizsgálatakor. Nézzük tehát az első két személy adatait. Fizetésükben 22 ezer forint különbség, míg az elégedettségükben 15 értéknyi különbség van. Ha feltételezzük, hogy az adatokból nyert „egyenes”, mint modell kiterjeszthető a „fizetés” dimenziójára, érdemes valamilyen egységben megadni a különbséget, legyen ez az egység a fizetés egy egysége. Tulajdonképpen azt szeretnénk tehát megtudni, hogy 1 egységnyi (ezerforintnyi) fizetés mekkora mértékben változtatja az elégedettséget. Ezt nagyon egyszerűen kiszámolhatjuk: ha 22 egységnyi fizetésbeli változáshoz 15 egységnyi elégedettségbeli változás tartozik, akkor 1 egységnyi fizetésbeli változáshoz 15/22=0,68 egységnyi elégedettségbeli változás tartozik. Vagyis, ha egy adatbázisban nem szereplő személynek 10 ezer forinttal több fizetése van, mint egy adatbázisban szereplő személynek, akkor az elégedettsége 10*0,68=6,8 ponttal magasabb, mint az adatbázisban szereplő személyé.